Exercices : Primitives et équations différentielles

Exercices corrigés

Exercice 1

La fonction $f$ est continue et dérivable sur $] 0 ; 5,5[$. Elle est représentée ci-dessous, ainsi que sa dérivée $f^{\prime}$, et l'une de ses primitives $F$. Associer à chaque courbe sa fonction.

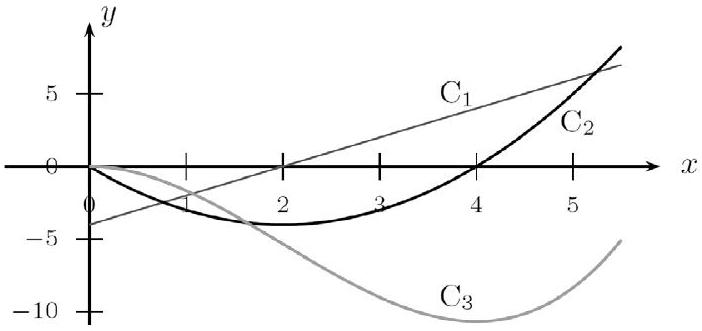
Corrigé

Nous allons utiliser le schéma de dérivation suivant :

$$ \mathrm{F} \longrightarrow f \longrightarrow f^{\prime} $$

Supposons alors que $C_{1}$ soit associé à la fonction $f$ ou à la fonction $F$. Comme $C_{1}$ est strictement croissante, sa dérivée $f^{\prime}$ (pour $f$ ) ou $f$ (pour $F$ ) serait strictement positive. Or aucune des 2 autres courbes n'est strictement positive.

Donc $C_{1}$ n'est associé ni à la fonction $f$, ni à la fonction $F$. Par élimination, il ne reste plus que $f^{\prime}$. $C_{1}$ est donc associé à la fonction $f^{\prime}$. Le signe de $f^{\prime}$ impose le sens de variation de $f$ selon le tableau suivant :

$x$	0		2	5,5
$f^{\prime}(x)$		-	0	+
	$f(x)$

Il est alors évident que seule la courbe $C_{2}$ peut être associée à $f$. Et par élimination, la courbe $C_{3}$ est nécessairement associée à $F$. Nous pouvons vérifier alors le tableau de variation suivant :

$x$	0		4	5,5
$\mathrm{~F}^{\prime}(x)=f(x)$	0	-	0	+
$\mathrm{F}(x)$

Exercice 2

Déterminer les primitives des fonctions suivantes sur $] 0 ;+\infty[$.

• $f(x)=5 x^{3}-2 x^{2}+4 x+9+\frac{17}{x}+\frac{29}{x^{2}}+e^{x}$
• $g(x)=(2 x+1) e^{x^{2}+x+8}$
• $h(x)=7 e^{7 x-4}+\frac{1}{x}$

Corrigé

• Réécrivons tout d'abord $f(x)$ pour faire apparaître des fonctions dont on connaît les primitives.

$$ f(x)=5 x^{3}-2 x^{2}+4 x+9+17 \frac{1}{x}+29 \frac{1}{x^{2}}+e^{x} $$

$f$ admet alors pour primitives : $F(x)=5 \frac{x^{4}}{4}-2 \frac{x^{3}}{3}+4 \frac{x^{2}}{2}+17 \ln x+29 \frac{-1}{x}+e^{x}+c \quad$ (où $\quad c \quad$ est une constante). Soit : $\quad F(x)=\frac{5 x^{4}}{4}-\frac{2 x^{3}}{3}+2 x^{2}+17 \ln x-\frac{29}{x}+e^{x}+c \quad$ (où $c \quad$ est une constante).

• On a : $g(x)=u^{\prime} e^{u}$ avec $u=x^{2}+x+8$ et $u^{\prime}=2 x+1$.

Par conséquent, $g$ admet des primitives du type $G=e^{u}+c$ (où $c$ est une constante). Soit : $G(x)=e^{x^{2}+x+8}+c$ (où $c$ est une constante).

• On a: $h(x)=u^{\prime} e^{u}+\frac{1}{x}$ avec $u=7 x-4$ et $u^{\prime}=7$.

Par conséquent, $h$ admet des primitives du type $H=e^{u}+\ln x+c$ (où $c$ est une constante). Soit : $H(x)=e^{7 x-4}+\ln x+c$ (où $c$ est une constante).

Exercice 3

Déterminer une primitive de chacune des fonctions suivantes sur $] 0 ;+\infty[$.

• $f(x)=\frac{2 x+1}{\left(x^{2}+x+6\right)^{2}}$
• $g(x)=\frac{10}{(2 x-3)^{2}}$
• $h(x)=7 e^{3 x-1}$

Corrigé

• On a $f=\frac{u^{\prime}}{u^{2}}$ avec $u=x^{2}+x+6$ et $u^{\prime}=2 x+1$.

Par conséquent, $f$ admet une primitive du type $F=\frac{-1}{u}$. Soit : $F(x)=\frac{-1}{x^{2}+x+6}$.

• Réécrivons tout d'abord $g(x)$ pour faire apparaître une fonction dont on connaît une primitive.

$$ g(x)=5 \frac{2}{(2 x-3)^{2}} $$

On a: $g(x)=5 \frac{u^{\prime}}{u^{2}} \quad$ avec $u=2 x-3$ et $u^{\prime}=2$. Par conséquent, $g$ admet une primitive du type $G=5 \frac{-1}{u}=\frac{-5}{u}$. Soit : $G(x)=\frac{-5}{2 x-3}$.

• Réécrivons tout d'abord $h(x)$ pour faire apparaître une fonction dont on connaît une primitive. On a : $h(x)=\frac{7}{3} 3 e^{3 x-1}$. Soit : $h(x)=\frac{7}{3} u^{\prime} e^{u}$ avec $u=3 x-1$ et $u^{\prime}=3$.

Par conséquent, $h$ admet une primitive du type $H=\frac{7}{3} e^{u}$. Soit : $H(x)=\frac{7}{3} e^{3 x-1}$.

Exercice 4

Soit $f$ définie par $f(x)=6 x^{2}+\frac{3}{x}$. Déterminer la primitive $F$ de $f$ sur $] 0 ;+\infty[$ telle que $F(1)=100$.

Corrigé

On a $f(x)=6 x^{2}+3 \frac{1}{x}$. Par conséquent, $f$ admet des primitives F telles que : $F(x)=6 \frac{x^{3}}{3}+3 \ln x+c$ (où $c$ est une constante). On réduit et on obtient : $F(x)=2 x^{3}+3 \ln x+c$ (où $c$ est une constante). Or : $F(1)=100 \Leftrightarrow 2 \times 1^{3}+3 \ln 1+c=100 \Leftrightarrow 2+3 \times 0+c=100$. Soit : $F(1)=100 \Leftrightarrow c=100-2=98$. Donc, la fonction F définie par $F(x)=2 x^{3}+3 \ln x+98$ sur $] 0 ;+\infty[$ est la primitive cherchée.

Exercice 5

Soit $g$ définie par $g(x)=\ln x \quad$ sur $] 0 ;+\infty[$. Soit $h$ définie par $h(x)=x \ln x-x+1 \quad$ sur $] 0 ;+\infty[$. Montrer que $h$ est la primitive de $g$ sur $] 0 ;+\infty[$ qui s'annule en 1.

Corrigé

Il suffit de montrer que $h^{\prime}=g$ sur $] 0 ;+\infty[$, et que $h(1)=0$. On a $h=u v-x+1$ avec $u=x, v=\ln x$, et par là : $u^{\prime}=1$ et $v^{\prime}=\frac{1}{x}$. Donc $h^{\prime}=u^{\prime} v+u v^{\prime}-1$. Soit : $\quad h^{\prime}(x)=1 \ln x+x \frac{1}{x}-1=\ln x+1-1=\ln x=g(x)$. Par conséquent, $h^{\prime}=g$ sur $] 0 ;+\infty[$, et $h$ est donc une primitive de $g$ sur $] 0 ;+\infty[$. Par aileurs : $h(1)=1 \ln 1-1+1=0$. Donc $h$ est la primitive de $g$ sur $] 0 ;+\infty[$ qui s'annule en 1.

Exercice 6

On considère l'équation différentielle (E) : $y^{\prime}=y+1-x$ sur $\mathbb{R}$.

1. Proposer une fonction $g$ définie sur $\mathbb{R}$ qui est solution de l'équation (E).
2. Montrer que $f$ est solution de (E) équivaut à $f-g$ solution de (E') : $y^{\prime}=y$.
3. En déduire les solutions de (E).

Corrigé

1. On note que $(\mathrm{E}) \Leftrightarrow y^{\prime}-y=1-x$.

Il est alors évident que la fonction $g(x)=x$ est solution de (E). Pour les sceptiques : $g^{\prime}(x)-g(x)=1-x$. 2. $f$ est solution de (E) si et seulement si $f^{\prime}(x)=f(x)+1-x$ si et seulement si $f^{\prime}(x)-f(x)=1-x$ si et seulement si $f^{\prime}(x)-f(x)=g^{\prime}(x)-g(x)$ si et seulement si $f^{\prime}(x)-g^{\prime}(x)=f(x)-g(x)$ si et seulement si $f-g$ solution de ( $\mathrm{E}^{\prime}$ ) : $y^{\prime}=y$. 3. Or les solutions de $y^{\prime}=y$ sont les fonctions $k e^{x}$ (où k est un réel quelconque).

Par conséquent : $f(x)-g(x)=k e^{x}$ (où k est un réel quelconque). Et par là : $f(x)=g(x)+k e^{x}$. Donc les fonctions $f(x)=x+k e^{x}$ (où k est un réel quelconque) sont les solutions de (E).

Exercice 7

Résoudre l'équation différentielle (E) : $2 y^{\prime}+y-7=0$ sur $\mathbb{R}$. Déterminer la solution $f$ de (E) telle que $f(0)=10$.

Corrigé

On a : (E) $\Leftrightarrow y^{\prime}=-0,5 y+3,5$. L'équation différentielle (E) sur $\mathbb{R}$ admet pour solution particulière la fonction $f$ définie par: $f(x)=-\frac{3,5}{-0,5}=7$. L'équation différentielle (E) sur $\mathbb{R}$ admet pour solutions les fonctions $f_{k}$ définies par : $f_{k}(x)=k \cdot e^{-0,5 x}+7$ (où $k$ est un réel), et ce sont les seules solutions.

On cherche alors la solution telle que $f(0)=10$. On a donc : $k \cdot e^{0}+7=10$, et donc : $k=3$.

Donc la solution cherchée est la fonction $f$ définie pour tout $x$ de $\mathbb{R}$ par : $f(x)=3 \cdot e^{-0,5 x}+7$.

Exercice 8

Partie A

Déterminer la solution $f$ de l'équation différentielle (E) : $y^{\prime}=3 y+5$ sur $\mathbb{R}$ telle que $f(0)=1$.

Partie B

On suppose dans ce qui suit que l'on ne connaît pas la formule explicite de $f$. On va toutefois déterminer des valeurs approchées des images par $f$ d'une séquence de nombres grâce à l'algorithme d'Euler. Les abscisses seront $0,0+\mathrm{h}, 0+2 \mathrm{~h}, \ldots, 0+\mathrm{nh}$, c'est-à-dire $0, \mathrm{~h}, 2 \mathrm{~h}, \ldots, \mathrm{nh}$ où h est un nombre strictement positif assez "petit" appelé "pas", et où $\mathrm{n}+1$ est le nombre total d'abscisses de la séquence. On rappelle que, puisque $f$ est dérivable sur $\mathbb{R}$, on a, pour tout nombre $x_{0}$, l'égalité : $\lim {h \rightarrow 0} \frac{f\left(x{0}+h\right)-f\left(x_{0}\right)}{h}=f^{\prime}\left(x_{0}\right)$. Et par là, on en déduit facilement l'approximation : $f\left(x_{0}+h\right) \approx f\left(x_{0}\right)+h f^{\prime}\left(x_{0}\right)$.

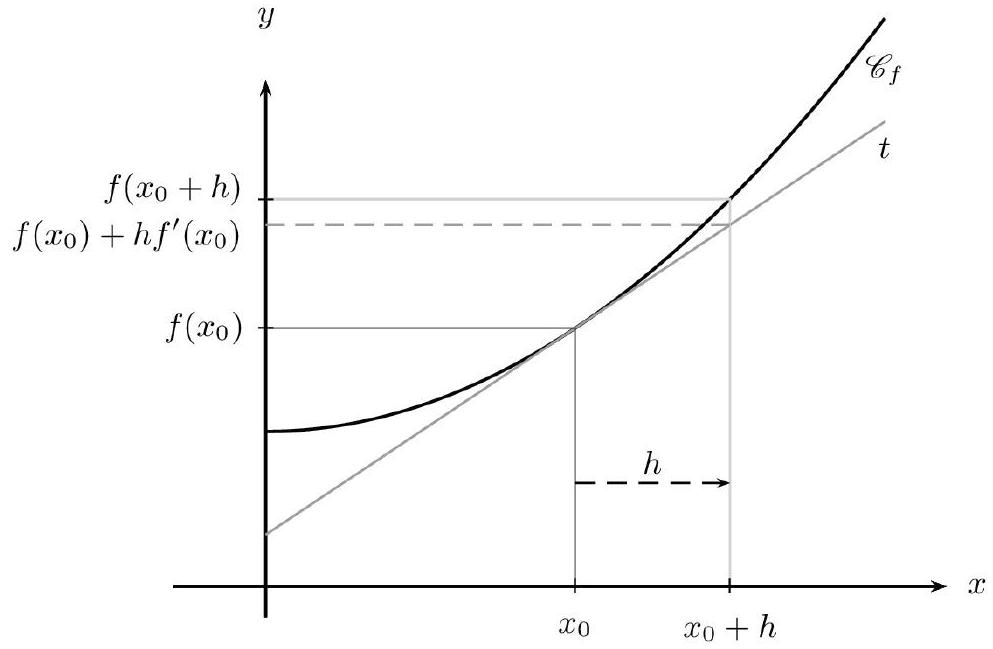
L'algorithme d'Euler utilise l'approximation précédente pour déterminer les images successives des abscisses de la séquence. À chaque itération, la valeur de $f^{\prime}\left(x_{0}\right)$ est donnée par l'égalité $f^{\prime}\left(x_{0}\right)=3 f\left(x_{0}\right)+5$. À la première itération, $x_{0}$ vaut 0 et $f\left(x_{0}\right)$ vaut 1. Concrètement :

La première abscisse de la séquence est 0 . Son image est 1 . La seconde abscisse de la séquence est $0+\mathrm{h}=\mathrm{h}$. Son image est $f(0+h) \approx f(0)+h f^{\prime}(0)$ avec $f^{\prime}(0)=3 f(0)+5$. La troisième abscisse de la séquence est $\mathrm{h}+\mathrm{h}=2 \mathrm{~h}$. Son image est $f(h+h) \approx f(h)+h f^{\prime}(h)$, avec $f^{\prime}(h)=3 f(h)+5$. La quatrième abscisse de la séquence est $2 \mathrm{~h}+\mathrm{h}=3 \mathrm{~h}$. Son image est $f(2 h+h) \approx f(2 h)+h f^{\prime}(2 h)$, avec $f^{\prime}(2 h)=3 f(2 h)+5$. La cinquième abscisse de la séquence est $3 \mathrm{~h}+\mathrm{h}=4 \mathrm{~h}$. Son image est $f(3 h+h) \approx f(3 h)+h f^{\prime}(3 h)$, avec $f^{\prime}(3 h)=3 f(3 h)+5$. Et ainsi de suite...

1. Voici ci-dessous un programme en python incomplet.

La fonction méthode_euler(x,y,h,n) doit retourner deux listes $X$ et $Y$ telles que : X contient la séquence des $\mathrm{n}+1$ abscisses $0, \mathrm{~h}, 2 \mathrm{~h}, \ldots \mathrm{nh}$ Y contient les valeurs approchées des images des éléments de X selon la méthode d'Euler.

3 def méthode_euler(x,y,h,n):# pour y'=3y+5
    X=[x]
    Y=[y]
    for k in
        x=X[k]
        y=Y[k]
        X.append(
        derivee=
        Y.append(y+derivee*h)
    return X,Y # X contient les abscisses des n+1 points, Y leurs ordonnées

Compléter les lignes incorrectes pour que le programme fonctionne correctement.

Ce qui suit n'est pas exigible, mais c'est intéressant ! Les experts doivent y réfléchir... 2. Compléter le programme pour qu'il affiche dans la console les listes retournées par méthode_euler(0,1,0.01,10). 3. Compléter le programme pour qu'il affiche la courbe représentative de $f$ et les points générés par méthode_euler(0,1,0.01,10).

Corrigé

Partie A

On a : $(\mathrm{E}) \Leftrightarrow y^{\prime}=3 y+5$ L'équation différentielle (E) sur $\mathbb{R}$ admet pour solution particulière la fonction $f$ définie par: $f(x)=-\frac{5}{3}$.

L'équation différentielle (E) sur $\mathbb{R}$ admet pour solutions les fonctions $f_{k}$ définies par : $f_{k}(x)=k \cdot e^{3 x}-\frac{5}{3}$ (où $k$ est un réel), et ce sont les seules solutions.

On cherche alors la solution telle que $f(0)=1$. On a donc $: k \cdot e^{0}-\frac{5}{3}=1$, et donc $: k=\frac{8}{3}$. Donc la solution cherchée est la fonction $f$ définie pour tout $x$ de $\mathbb{R}$ par : $f(x)=\frac{8}{3} \cdot e^{3 x}-\frac{5}{3}$.

Partie B

1. Voici un programme convenable.

def méthode_euler(x,y,h,n):# pour }\mp@subsup{y}{}{\prime}=3y+
    X=[x]
    Y=[y]
    for k in range(n):# n boucles
        X=X[k]
        y=Y[k]
        X.append(x+h)
        derivee=3*Y[k]+5
        Y.append(y+derivee*h)
    return X,Y # X contient les abscisses des n+1 points, Y leurs ordonnées

2. et 3. Et pour obtenir les sorties demandées, voici ci-après une proposition.

1 from math import*
2 from matplotlib.pylab import*
3 def méthode_euler(x,y,h,n):# pour y'=3y+5
    X=[x]
    Y=[y]
    for k in range(n):# n boucles
        X=X[k]
        y=Y[k]
        X.append(x+h)
        derivee=3*Y[k]+5
        Y.append(y+derivee*h)
    return X,Y # X contient les abscisses des n+1 points, Y leurs ordonnées
X,Y=méthode_euler(0,1,0.01,10) # y(0)=1, pas=0.01, 11 points en tout
print(X,Y)
plot(X,Y,"r.") # les points sont rouges et non reliés
8
X=arange(0,0.11,0.01) # séquence des nombres de 0 à 0.11 (exclu) par pas de 0.01
Y=(8/3)*e**(3*X)-(5/3) # images des élts de X par la sol de y'=3y+5 tq y(0)=1
plot(X,Y,"g") # les points sont verts et reliés
2
show()
close()

La ligne 14 affecte aux listes $X$ et $Y$ les valeurs demandées. Ainsi, la liste X va contenir les nombres $0,0.01,0.02,0.03, \ldots$ etc, jusqu'à 0.1 (en pratique 0.09999999999999999 à cause des approximations en binaire).

La liste Y va contenir les images (approchées) des nombres précédents, à savoir 1, 1.08, 1.1624, 1.2472720000000002 , ... jusqu'à 1.9171103449176587.

La ligne 15 affiche les deux listes dans la console. Les lignes 17 à 23 permettent de créer le graphique demandé. La ligne 24 permet de l'afficher à l'écran. Et voici la sortie graphique !

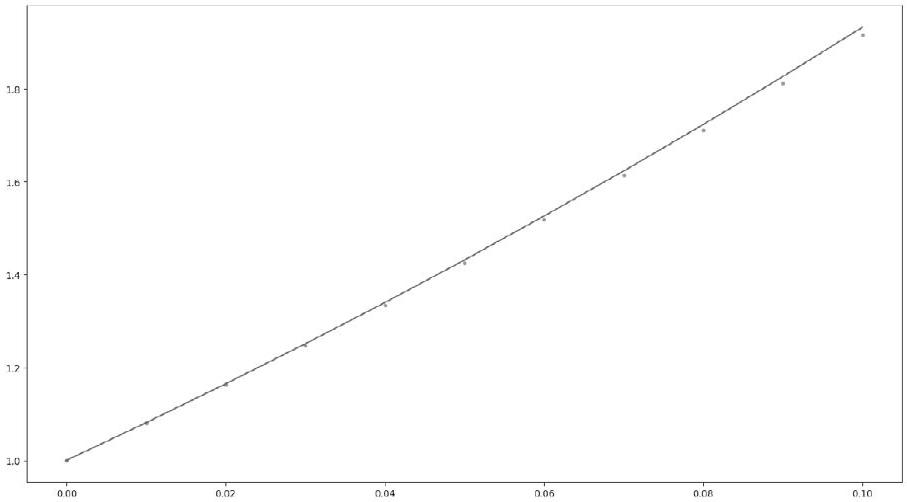
Plus les abscisses augmentent, plus l'ordonnée du point obtenu s'éloigne de l'ordonnée du point de la courbe.

Exercice 9

Partie A

Soit $a$ un réel fixé. On considère l'équation différentielle (E) : $y^{\prime}-a y=x$ sur $[0 ;+\infty[$.

1. On suppose que la fonction $g$ définie sur $\left[0 ;+\infty\left[\operatorname{par} g(x)=\frac{1}{2} x-\frac{1}{4}\right.\right.$ est solution de l'équation différentielle (E). Montrer que, nécessairement, $a=-2$.
2. Déterminer les solutions de $(\mathrm{E}): y^{\prime}+2 y=x$ sur $[0 ;+\infty[$.
3. Soit $f$ la solution de l'équation différentielle (E) telle que : $f(0)=\frac{11}{4}$.

Montrer que $f$ est définie, pour tout $x$ de $\left[0 ;+\infty\left[\right.\right.$, par : $f(x)=3 e^{-2 x}+\frac{1}{2} x-\frac{1}{4}$. 4. Vérifier que : $f\left(\frac{1}{2}\right)=\frac{3}{e}$.

Partie B

On rappelle que la fonction $f$ citée dans la partie A est définie, pour tout $x$ de $[0 ;+\infty[$, par: $f(x)=3 e^{-2 x}+0,5 x-0,25$.

1. Déterminer $\lim _{x \rightarrow+\infty} f(x)$.
2. Dresser le tableau de variation de $f$ sur $[0 ;+\infty[$.

Vérifier que $f$ admet un minimum en $\ln \frac{12}{2}$. 3. Montrer que l'équation $f(x)=\frac{3}{e}$ admet exactement 2 solutions $\alpha$ et $\beta$ sur $[0 ;+\infty[$ (avec $\alpha<\beta$ ). 4. Quelle est la valeur de $\alpha$ ? 5. $\beta$ est donc la plus grande des 2 solutions de l'équation $f(x)=\frac{3}{e}$.

Soit $\left[x_{1} ; x_{2}\right]$ un intervalle contenant $\beta$ tel que $x_{2}-x_{1}=0,1$. La fonction intervalle() du programme suivant, écrit en Python, devrait retourner une liste contenant deux nombres $x_{1}$ et $x_{2}$ convenables.

1from math import*
2def f(x):
3 y=
4 return y
5def intervalle():
    x=log(12)/2
    while f(x)<3/e:
        x=x+0.05
    return
|OS=intervalle()

Compléter les lignes 3, 7 et 9 pour que le programme soit fonctionnel. Donner la liste que contient la variable $S$ après exécution du programme.

Corrigé

Partie A

1. On a : $(\mathrm{E}) \Leftrightarrow y^{\prime}=a y+x$ sur $[0 ;+\infty[$.

Comme : $g(x)=\frac{1}{2} x-\frac{1}{4}$, on obtient : $g^{\prime}(x)=\frac{1}{2}$. Et comme $g$ est solution de (E), on obtient : $g^{\prime}(x)=a g(x)+x$. Soit : $\frac{1}{2}=a\left(\frac{1}{2} x-\frac{1}{4}\right)+x$. Soit : $0=\frac{a}{2} x-\frac{a}{4}+x-\frac{1}{2}$. Soit : $\left(\frac{a}{2}+1\right) x-\frac{a}{4}-\frac{1}{2}=0$. Et cette égalité est vraie pour tout $x$ de $[0 ;+\infty[$. En particulier, pour $x=0$, cela donne : $-\frac{a}{4}-\frac{1}{2}=0$. Et par là, nécessairement, $a=-2$. Les inquiets peuvent vérifier que $g$ est effectivement solution de $(E): y^{\prime}=-2 y+x$ en constatant que : pour tout $x$ de $\left[0 ;+\infty\left[\right.\right.$, on a bien : $g^{\prime}(x)=-2 g(x)+x$. 2. On a $(\mathrm{E}) \Leftrightarrow y^{\prime}=-2 y+x$ sur $[0 ;+\infty[$.

Les solutions de $y^{\prime}=-2 y$ sont les fonctions $k e^{-2 x}$ (où k est un réel quelconque). Or $g(x)=\frac{1}{2} x-\frac{1}{4}$ est une solution particulière de l'équation différentielle (E). Donc les fonctions $y=\frac{1}{2} x-\frac{1}{4}+k e^{-2 x}$ (où k est un réel quelconque) sont les solutions de (E). 3. $f$ est solution de l'équation différentielle (E).

Donc il existe un réel $k$ tel que $f(x)=\frac{1}{2} x-\frac{1}{4}+k e^{-2 x}$. Or $f(0)=\frac{11}{4}$. Donc : $\frac{1}{2} \times 0-\frac{1}{4}+k e^{-2 \times 0}=\frac{11}{4}$. Soit: $-\frac{1}{4}+k=\frac{11}{4}$. Et par là : $k=3$. Par conséquent, on a bien : $f(x)=3 e^{-2 x}+\frac{1}{2} x-\frac{1}{4}$ (pour tout $x$ de $[0 ;+\infty[$ ) c.q.f.d. 4. On calcule : $f\left(\frac{1}{2}\right)=3 e^{-2 \times \frac{1}{2}}+\frac{1}{2} \times \frac{1}{2}-\frac{1}{4}=3 e^{-1}=\frac{3}{e}$. c.q.f.d.

Partie B

On admet que la fonction $f$ citée dans la partie A est définie, pour tout $x$ de $[0 ;+\infty[$, $\operatorname{par} f(x)=3 e^{-2 x}+0,5 x-0,25$. Soit C sa courbe représentative.

1. On a: $\lim _{x \rightarrow+\infty}-2 x=-\infty$.

Or: $\lim _{X \rightarrow-\infty} e^{X}=0$. Donc : $\lim _{x \rightarrow+\infty} 3 e^{-2 x}-0,25=3 \times 0-0,25=-0,25$. Or, par ailleurs, on a : $\lim _{x \rightarrow+\infty} 0,5 x=+\infty$. Donc finalement, on obtient : $\lim _{x \rightarrow+\infty} f(x)=+\infty$. 2. On dérive : $f^{\prime}(x)=3 \times(-2) e^{-2 x}+0,5=-6 e^{-2 x}+0,5$.

On résout alors : $f^{\prime}(x)>0 \Leftrightarrow-6 e^{-2 x}+0,5>0 \Leftrightarrow-6 e^{-2 x}>-0,5$. Soit : $f^{\prime}(x)>0 \Leftrightarrow e^{-2 x}<\frac{-0,5}{-6}$. Soit : $f^{\prime}(x)>0 \Leftrightarrow \ln e^{-2 x}<\ln \frac{1}{12}$. Soit : $f^{\prime}(x)>0 \Leftrightarrow-2 x<\ln \frac{1}{12}$. Soit : $f^{\prime}(x)>0 \Leftrightarrow x>\frac{\ln \frac{1}{12}}{-2}$.

Soit : $f^{\prime}(x)>0 \Leftrightarrow x>\frac{\ln 12}{2}$. Il est alors évident que : $f^{\prime}(x)=0 \Leftrightarrow x=\frac{\ln 12}{2}$ Et nous obtenons le tableau de variation de $f$ sur $[0 ;+\infty[$ qui suit.

$x$	0		$\frac{\ln 12}{2}$	$+\infty$
$f^{\prime}(x)$		-	0	+
	$\frac{11}{4}$
$f(x)$
				${ }_{f\left(\frac{\ln 12}{2}\right)}$

On vérifie que $f$ admet effectivement un minimum en $\ln \frac{12}{2}$. Pour la suite, on note que $f(0)=\frac{11}{4}=2,75$ et $f\left(\frac{\ln 12}{2}\right) \approx 0,62$. 3. D'après le tableau de variation précédent, la fonction $f$ est continue et strictement décroissante sur $\left[0 ; \frac{\ln 12}{2}\right]$. Comme $f(0)=2,75, \quad \frac{3}{e} \approx 1,10 \quad$ et $\quad f\left(\frac{\ln 12}{2}\right) \approx 0,62$, on a : $f(0)<\frac{3}{e}<f\left(\frac{\ln 12}{2}\right)$. On peut appliquer le théorème de la bijection. On en déduit que l'équation $f(x)=\frac{3}{e}$ admet exactement 1 solution $\alpha$ sur $\left[0 ; \frac{\ln 12}{2}\right]$ (et on a : $0<\alpha<\frac{\ln 12}{2}$ ). De même, on peut montrer que $f(x)=\frac{3}{e}$ admet exactement 1 solution $\beta$ sur $\left[\frac{\ln 12}{2},+\infty[\right.$ (et on a: $\frac{\ln 12}{2}<\beta$ ). Donc finalement, l'équation $f(x)=\frac{3}{e}$ admet exactement 2 solutions $\alpha$ et $\beta$ sur $[0 ;+\infty[(\operatorname{avec} \alpha<\beta) \quad$ c.q.f.d. 4. On a vu que $f(0,5)=\frac{3}{e}$, et $\alpha$ est l'unique solution de l'équation $f(x)=\frac{3}{e}$ telle que $0<\alpha<\frac{\ln 12}{2}$. Donc $\alpha=0,5$. 5. $\beta$ est la solution de l'équation $f(x)=\frac{3}{e}$ strictement supérieure à $\frac{\ln 12}{2}$. $\left[x_{1} ; x_{2}\right]$ est un intervalle contenant $\beta$ tel que $x_{2}-x_{1}=0,1$. La fonction intervalle() du programme suivant, écrit en Python, retourne une liste contenant deux nombres $x_{1}$ et $x_{2}$ convenables.

1from math import*
2def f(x):
3 y = 3 * e ^ { * * } ( - 2 * x ) + 0 . 5 * x - 0 . 2 5
4 return y
5def intervalle():
6 x = \operatorname { l o g } ( 1 2 ) / 2
7 while f(x)<3/e:
        x=x+0.05
9 return [x-0.1,x]
S=intervalle()
1 1
2 print(S)

Après exécution du programme, la variable S vaut $\left[x_{1}, x_{2}\right]$ avec $x_{1} \approx 2,6$ et $x_{2} \approx 2,7$. La ligne 12, non demandée, permet d'afficher la valeur de S dans la console. Il s'affiche : [2.5924533248939983, 2.6924533248939984]

Exercice 10

Partie A

On considère un corps radioactif M . Soit $y(t)$ la masse totale des noyaux radioactifs du corps M à l'intant $t$ (en secondes). On suppose que $y(0)=1$ (en grammes). On admet que $y$ est solution de l'équation différentielle (E) : $y^{\prime}=-\lambda y$ sur [ $0 ;+\infty$ [, où $\lambda$ est un réel strictement positif appelé constante radioactive.

1. Déterminer l'expression de $y(t)$ pour $t \geq 0$.
2. Les physiciens ont remarqué que :

• d'une part, le nombre de noyaux radioactifs (instables) du corps $M$ ne fait que diminuer,
• d'autre part, la décroissance radioactive semble se poursuivre jusqu'à ce que tous les noyaux de l'échantillon soient stables. La fonction $y(t)$ déterminée précédemment fournit-elle un modèle corroboré par ces constatations?

3. La demi-vie est le temps $T$ nécessaire pour que la moitié des noyaux radioactifs se désintègrent. Exprimer $T$ en fonction de $\lambda$.
4. Pour le carbone 14 , la demi-vie est de 5730 années.

On admettra qu'une année contient 365,25 jours en moyenne. Montrer que, dans ce cas, $\lambda \approx 3,833 \times 10^{-12}$ (en $s^{-1}$ ). 5. L'activité $A(t)$ à la date $t$ d'un échantillon contenant N noyaux radioactifs est le nombre moyen de désintégrations par seconde. Son unité dans le Système international est le becquerel (1 Bq correspond à une désintégration par seconde). Elle se mesure à l'aide d'un compteur Geiger-Müller.

On a alors $A(t)=-k y^{\prime}(t)$, où k est le nombre de noyaux radioactifs par gramme. Sachant qu'un gramme de carbone 14 pur contient environ $6,022 \times \frac{10^{23}}{14}$ noyaux radioactifs, montrer que l'activité d'un gramme de carbone 14 pur est d'environ $165 \times 10^{9}$ Bq.

Partie B

On désire modéliser le problème de la partie A à l'aide de suites. Pour simplifier, on se restreint au cas bien connu du carbone 14. Soit $u_{n}$ le nombre de noyaux radioactifs (instables) du corps M au bout de $n$ secondes. On pose $u_{0}=N_{0}$. On suppose que, pour tout entier naturel $n$, on a : $u_{n+1}-u_{n}=-\lambda u_{n}\left(\right.$ où $\lambda \approx 3,833 \times 10^{-12}\left(\right.$ en $\left.\left.s^{-1}\right)\right)$.

1. Déterminer la nature de la suite $\left(u_{n}\right)$.

Donner son expression explicite en fonction de $N_{0}$. 2. Montrer que la suite $\left(u_{n}\right)$ est strictement décroissante. 3. Déterminer $\lim {n \rightarrow+\infty} u{n}$. 4. Retrouver la valeur de l'activité d'un gramme de carbone 14 pur (voir partie A 5.). 5. Soit ( $v_{n}$ ) la suite donnant le nombre de noyaux radioactifs (instables) du corps M au bout de $n$ années. Une année représente en moyenne $365,25 \times 24 \times 3600=31557600$ secondes. Montrer que $\left(v_{n}\right)$ est géométrique. Exprimer sa raison $b$ en fonction de $\lambda$. Par la suite, on prendra : $b \approx 0,9998790$. 6. On a retrouvé un squelette dont la proportion en carbone 14 est égale à $10 %$ de celle d'un squelette similaire actuel. Après exécution.du programme suivant, en Python, la variable age doit contenir l'âge du squelette fossile, en années.

1def années(taux):
    v=1
    n=0
    while
        v=v*
        n=n+1
    return n
8 \text { age= }

Corriger les 4 lignes incomplètes pour que ce programme fonctionne correctement.

Corrigé

Partie A

1. L'équation différentielle (E) : $y^{\prime}=-\lambda y$ sur $[0 ;+\infty[$ a pour solutions les fonctions $y_{k}$ définies par : $y_{k}(t)=k \cdot e^{-\lambda t}$ (où $k$ est un réel), et ce sont les seules solutions.

On cherche alors la solution telle que $y(0)=1$. On a donc : $k \cdot e^{0}=1$, et donc : $k=1$. Donc la solution cherchée est la fonction $y$ définie pour tout $t$ de $[0 ;+\infty[$ par : $y(t))=e^{-\lambda t}$. 2. On note que : $y^{\prime}(t)=-\lambda y(t)=-\lambda e^{-\lambda t}$.

Et comme $\lambda$ est un réel strictement positif, et qu'un exponentielle est strictement positive, $y^{\prime}(t)$ est strictement négative (pour tout $t$ de $[0 ;+\infty[$ ). Par conséquent, la fonction $y$ est strictement décroissante. Donc, effectivement, le nombre de noyaux radioactifs (instables) du corps M ne fait que diminuer.

Par ailleurs, $\lim _{t \rightarrow+\infty}(-\lambda t)=-\infty$. Or: $\lim _{X \rightarrow-\infty} e^{X}=0$. Donc : $\lim _{t \rightarrow+\infty} y(t)=0$. Le nombre de noyaux instables tend vers 0 . Donc, effectivement, la décroissance radioactive se poursuit jusqu'à ce que tous les noyaux de l'échantillon soient stables.

En conclusion, la fonction $y(t)$ déterminée précédemment fournit donc un modèle en accord avec les observations. 3. La demi-vie $T$ est solution de l'équation : $y(T)=0,5$.

Or : $e^{-\lambda T}=0,5 \Leftrightarrow-\lambda T=\ln 0,5 \Leftrightarrow T=\frac{\ln 0,5}{-\lambda}=\frac{-\ln 2}{-\lambda}$. Donc : $T=\frac{\ln 2}{\lambda}$. 4. On a immédiatement : $\lambda=\frac{\ln 2}{T}$.

Pour le carbone 14, on a : $T=5730 \times 365,25 \times 24 \times 3600 \approx 1,808 \times 10^{11}(\mathrm{en}$ secondes). Et par là : $\lambda \approx \frac{\ln 2}{1,808 \times 10^{11}} \approx 3,833 \times 10^{-12}\left(\right.$ en $\left.s^{-1}\right)$. 5. L'activité d'un gramme de carbone 14 pur est $A(0)=-k \times y^{\prime}(0)=-k \times\left(-\lambda e^{-\lambda \times 0}\right)=k \lambda$. Or, comme $k \approx 6,022 \times \frac{10^{23}}{14}$ et $\lambda \approx 3,833 \times 10^{-12}$, on obtient : $A(0) \approx 1,65 \times 10^{11}$.

L'activité d'un gramme de carbone 14 pur est bien d'environ $165 \times 10^{9} \mathrm{~Bq}$.

Partie B

1. $u_{n+1}-u_{n}=-\lambda u_{n} \Leftrightarrow u_{n+1}=(1-\lambda) u_{n}$.

Donc il existe un réel $a=1-\lambda$ tel que, pour tout entier naturel $n$, on a : $u_{n+1}=a u_{n}$. La suite ( $u_{n}$ ) est donc géométrique de raison $a$. Et par là : $u_{n}=u_{0} \times a^{n}$. Soit : $u_{n}=N_{0} \times a^{n}$ avec $a \approx 1-3,833 \times 10^{-12}$. 2. On a donc : $u_{n}=N_{0} \times a^{n}$.

Notons que, comme $a=1-\lambda$, et que $\lambda \approx 3,833 \times 10^{-12}$, il est clair que $0<a<1$. Donc la suite ( $a^{n}$ ) est strictement décroissante. Et comme $N_{0}$ est strictement positif, la suite ( $u_{n}$ ) est également strictement décroissante. 3. Comme $0<a<1$, on obtient : $\lim {n \rightarrow+\infty} u{n}=N_{0} \times 0=0$. 4. L'activité $A(0)$ d'un gramme de carbone 14 pur est $u_{0}-u_{1}$.

Or $u_{0}=N_{0} \approx 6,022 \times \frac{10^{23}}{14}$. et $u_{1}=N_{0} \times a \approx 6,022 \times \frac{10^{23}}{14}\left(1-3,833 \times 10^{-12}\right)$. Donc : $A(0) \approx 6,022 \times \frac{10^{23}}{14}\left(1-\left(1-3,833 \times 10^{-12}\right)\right) \approx 1,65 \times 10^{11}$. L'activité d'un gramme de carbone 14 pur est toujours d'environ $165 \times 10^{9} \mathrm{~Bq}$. 5. Un année représente 31557600 secondes.

Par conséquent, $v_{n+1}=v_{n} \times a^{31557600}$. Soit : $v_{n+1} \approx v_{n} \times b$ avec $b \approx(1-\lambda)^{31557600}$. Par la suite, on prendra : $b \approx 0,9998790$. 6. Les lignes corrigées sont les lignes $4,5,7$ et 8 .

Voici un programme correct.

1def années(taux):
    v=1
    n=0
    while v>taux:
        v=v*0.9998790
        n=n+1
    return n
8 age=années (0.1)
9
10 print(age)

La ligne 10, non demandée, permet d'afficher l'âge demandé dans la console. Il s'affiche 19029. Le squelette a environ 19000 ans.