Cours : Fonctions sinus et cosinus
Fonctions sinus et cosinus
Quelques rappels de première.
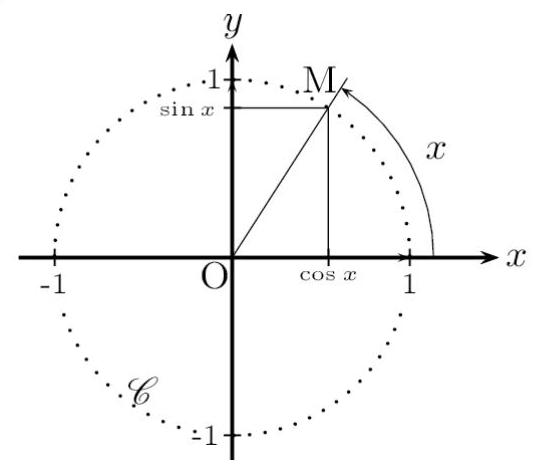
Pour tout réel $x$ : $-1 \leq \cos x \leq 1 \quad-1 \leq \sin x \leq 1 \quad \cos ^{2} x+\sin ^{2} x=1$ $\cos (-x)=\cos x \quad \sin (-x)=-\sin x$ $\cos (\pi-x)=-\cos x \quad \sin (\pi-x)=\sin x$ $\cos (\pi+x)=-\cos x \quad \sin (\pi+x)=-\sin x$ $\cos \left(\frac{\pi}{2}-x\right)=\sin x \quad \sin \left(\frac{\pi}{2}-x\right)=\cos x$
Pour tout $k$ entier relatif $\quad \sin (x+2 k \pi)=\sin x \quad \cos (x+2 k \pi)=\cos x$
Et voici le cours de terminale.
Définition
La fonction sinus est la fonction définie sur $\mathbb{R}$ qui, à tout réel $x$ associe $\sin x$. La fonction cosinus est la fonction définie sur $\mathbb{R}$ qui, à tout réel $x$ associe $\cos x$.
Propriétés
La fonction $\sin x$ admet pour dérivée $\cos x$ sur $\mathbb{R}$. Ainsi : $(\sin x)^{\prime}=\cos x$. La fonction $\cos x$ admet pour dérivée $-\sin x$ sur $\mathbb{R}$. Ainsi : $(\cos x)^{\prime}=-\sin x$.
Propriétés
Les fonctions sinus et cosinus sont continues sur $\mathbb{R}$.
Les fonctions sinus et cosinus sont périodiques de période $2 \pi$ sur $\mathbb{R}$. Par conséquent, pour tout $x$ réel et tout $k$ entier relatif, on a :
$$ \sin (x+2 k \pi)=\sin x \quad \text { et } \quad \cos (x+2 k \pi)=\cos x . $$
Et par là, dans un repère ( $O, \vec{\imath}, \vec{\jmath}$ ), les courbes représentatives des fonctions sinus et cosinus sont invariantes par toute translation de vecteur $k 2 \pi \vec{\imath}$.
La fonction sinus est impaire sur $\mathbb{R}$. Par conséquent, pour tout $x$ réel, $\sin (-x)=-\sin x$. Et par là, la courbe représentative de la fonction sinus est symétrique par rapport à l'origine. La fonction cosinus est paire sur $\mathbb{R}$. Par conséquent, pour tout $x$ réel, $\cos (-x)=\cos x$. Et par là, dans un repère orthogonal, la courbe représentative de la fonction cosinus est symétrique par rapport à l'axe des ordonnées.
Les fonctions sinus et cosinus vérifient les tableaux de variation ci-dessous.
| $x$ | 0 | $\frac{\pi}{2}$ | $\pi$ |
|---|---|---|---|
| 1 | |||
| $\cos (x)$ | 0 | ||
| -1 |
| $x$ | 0 | $\frac{\pi}{2}$ | $\pi$ |
|---|---|---|---|
| $\sin (x)$ | $\pi^{1}$ | ||
| 0 |
Les fonctions sinus et cosinus vérifient les tableaux de signes ci-dessous.
| $x$ | 0 | $\frac{\pi}{2}$ | $\pi$ |
|---|---|---|---|
| $\cos (x)$ | +0 | - |
| $x$ | 0 | $\pi$ |
|---|---|---|
| $\sin (x)$ | $0+\phi$ |
Les fonctions sinus et cosinus vérifient les tableaux de valeurs ci-dessous.
| $x$ | 0 | $\frac{\pi}{6}$ | $\frac{\pi}{4}$ | $\frac{\pi}{3}$ | $\frac{\pi}{2}$ |
|---|---|---|---|---|---|
| $\sin x$ | 0 | 0,5 | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | 1 |
| $\cos x$ | 1 | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | 0,5 | 0 |
Ces tableaux de valeurs s'étendent à $[0 ; \pi]$ en utilisant les angles associés, qui fournissent les égalités : $\sin (\pi-x)=\sin (x)$ et $\cos (\pi-x)=-\cos (x)$.
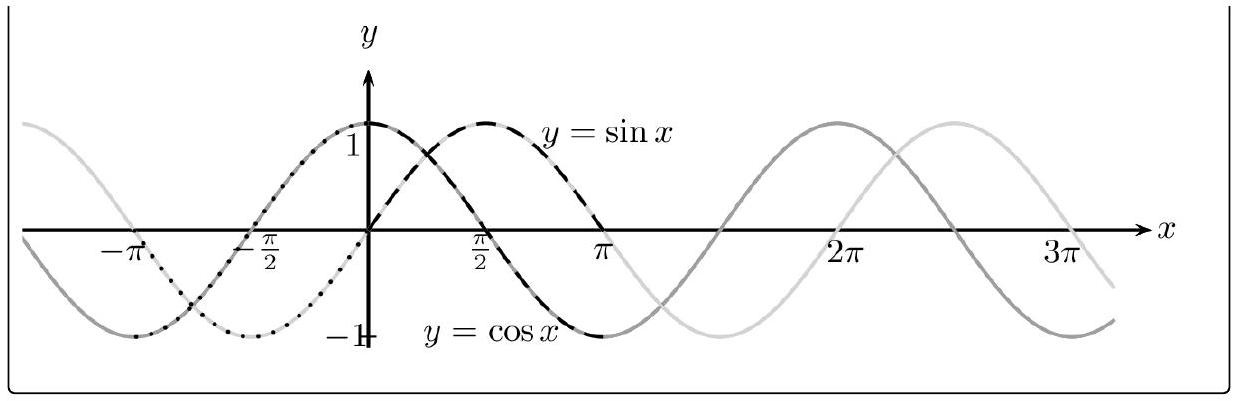
On obtient chacune des courbes qui suivent à partir d'un tracé sur $[0 ; \pi]$, étendu par symétrie sur $[-\pi ; \pi]$, et répété à l'infini par translations successives.
Ces courbes s'appellent des sinusoïdes.
Limite de référence
$\lim _{x \rightarrow 0} \frac{\sin x}{x}=1$
