Cours : Limites de fonctions
Limites de fonctions
I Limites en $+\infty$ ou en $-\infty$
Limite infinie en $+\infty$ ou en $-\infty$
La fonction $f$ a pour limite $+\infty$ en $+\infty$ lorsque tout intervalle du type $] A ;+\infty[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$ pour $x$ assez «grand».
On note $\lim _{x \rightarrow+\infty} f(x)=+\infty$.
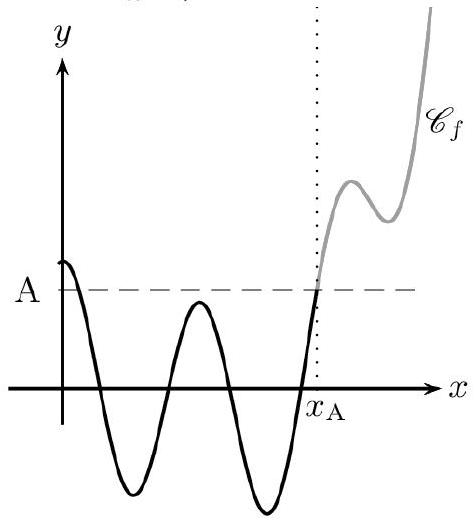
La fonction $f$ a pour limite $-\infty$ en $+\infty$ lorsque tout intervalle du type $]-\infty$; $A$ [ (où $A$ est un réel) contient toutes les valeurs de $f(x)$ pour $x$ assez «grand». On note $\lim _{x \rightarrow+\infty} f(x)=-\infty$.
La fonction $f$ a pour limite $+\infty$ en $-\infty$ lorsque tout intervalle du type $] A ;+\infty[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$ pour $x$ assez «négatif». On note $\lim _{x \rightarrow-\infty} f(x)=+\infty$.
La fonction $f$ a pour limite $-\infty$ en $-\infty$ lorsque tout intervalle du type $]-\infty$; $A$ [ (où $A$ est un réel) contient toutes les valeurs de $f(x)$ pour $x$ assez « négatif». On note $\lim _{x \rightarrow-\infty} f(x)=-\infty$.
Limites de référence
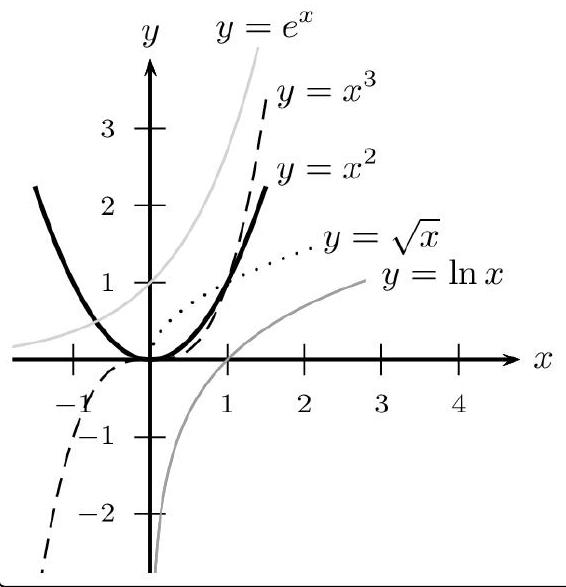
$\lim _{x \rightarrow+\infty} x=+\infty \quad \lim _{x \rightarrow+\infty} x^{2}=+\infty \quad \lim _{x \rightarrow+\infty} x^{n}=+\infty \quad($ pour $n \in \mathbb{N}$ et $n>0)$
$$ \left\lvert, \begin{aligned} & \lim _{x \rightarrow+\infty} \sqrt{x}=+\infty \ & \lim _{x \rightarrow-\infty} x=-\infty \quad \lim _{x \rightarrow-\infty} x^{2}=+\infty \quad \lim _{x \rightarrow-\infty} x^{3}=-\infty \ & \lim _{x \rightarrow+\infty} e^{x}=+\infty \quad \lim _{x \rightarrow+\infty} \frac{e^{x}}{x}=+\infty \quad \lim _{x \rightarrow+\infty} \frac{e^{x}}{x^{n}}=+\infty(\text { pour } n \in \mathbb{N}) \end{aligned}\right. $$
Fonction vue en terminale
$\lim _{x \rightarrow+\infty} \ln x=+\infty$
Limite finie en $+\infty$ ou en $-\infty$
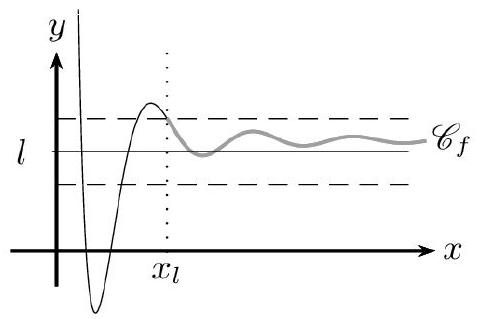
La fonction $f$ a pour limite $l$ en $+\infty$ lorsque tout intervalle ouvert contenant $l$ contient toutes les valeurs de $f(x)$ pour $x$ assez «grand».
On note $\lim _{x \rightarrow+\infty} f(x)=l$.
On dit que, dans un repère, la droite $d$ d'équation $y=l$ est asymptote horizontale en $+\infty$ à la courbe représentative C de $f$.
La fonction $f$ a pour limite $l$ en $-\infty$ lorsque tout intervalle ouvert contenant $l$ contient toutes les valeurs $f(x)$ pour $x$ assez « négatif». On note $\lim _{x \rightarrow-\infty} f(x)=l$.
On dit que, dans un repère, la droite $d$ d'équation $y=l$ est asymptote horizontale en $-\infty$ à la courbe représentative C de $f$.
Fonction constante
Soit $l$ un nombre réel; si $f(x)=l$, alors $\lim _{x \rightarrow+\infty} f(x)=\lim _{x \rightarrow-\infty} f(x)=l$.
Limites de référence
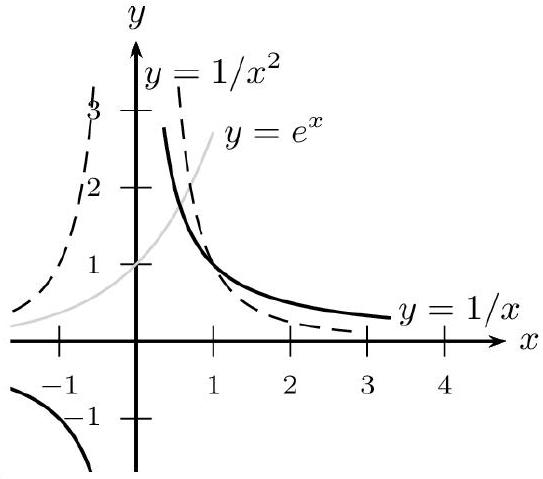
$\lim _{x \rightarrow+\infty} \frac{1}{x}=\lim _{x \rightarrow-\infty} \frac{1}{x}=0 \quad \lim _{x \rightarrow+\infty} \frac{1}{x^{2}}=\lim _{x \rightarrow-\infty} \frac{1}{x^{2}}=0$ $\lim _{x \rightarrow+\infty} \frac{1}{x^{n}}=\lim _{x \rightarrow-\infty} \frac{1}{x^{n}}=0(\operatorname{pour} n \in \mathbb{N}$ et $n>0) \quad \lim _{x \rightarrow+\infty} \frac{1}{\sqrt{x}}=0$ $\lim _{x \rightarrow-\infty} e^{x}=0 \quad \lim _{x \rightarrow-\infty} x e^{x}=0 \quad \lim _{x \rightarrow-\infty} x^{n} e^{x}=0($ pour $n \in \mathbb{N})$
Fonction vue en terminale
$\lim _{x \rightarrow+\infty} \frac{\ln x}{x}=0$
Unicité
Si elle existe, la limite d'une fonction en l'infini est unique.
II Limites en a
Limite infinie en un nombre réel $\boldsymbol{a}$
La fonction $f$ a pour limite $+\infty$ en a lorsque tout intervalle du type $] A ;+\infty[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$ pour $x$ assez «proche» de $a$.
On note : $\lim _{x \rightarrow a} f(x)=+\infty$.
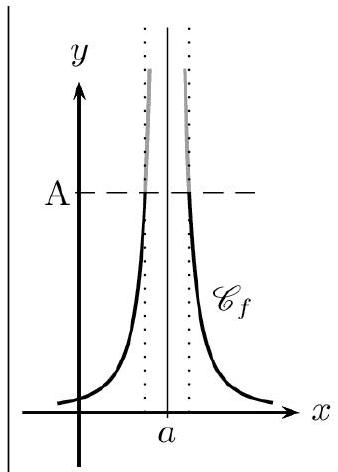
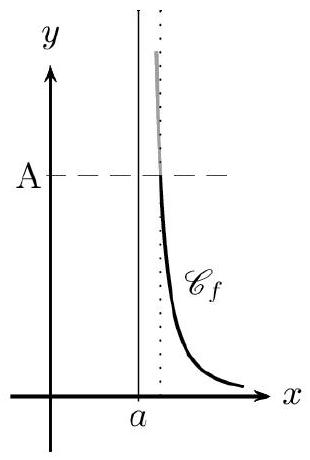
La fonction $f$ a pour limite $+\infty$ à droite en a lorsque tout intervalle du type $] A ;+\infty[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$ pour $x$ assez «proche» de $a$ tout en restant supérieur à $a$.
On note : $\lim _{\substack{x \rightarrow a \ x>a}} f(x)=+\infty$.
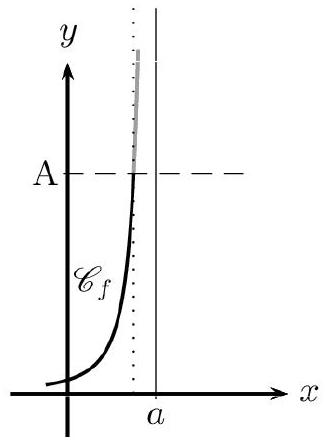
La fonction $f$ a pour limite $+\infty$ à gauche en $a$ lorsque tout intervalle du type $] A ;+\infty[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$ pour $x$ assez «proche» de $a$ en restant inférieur à $a$.
On note : $\lim _{\substack{x \rightarrow a \ x<a}} f(x)=+\infty$.
On définit de façon analogue une limite $-\infty$ en $a$, à droite en $a$, ou à gauche en $a$.
Dans tous les cas précédents, on dit que, dans un repère, la droite $d$ d'équation $x=a$ est asymptote verticale en $a$ à la courbe représentative C de $f$.
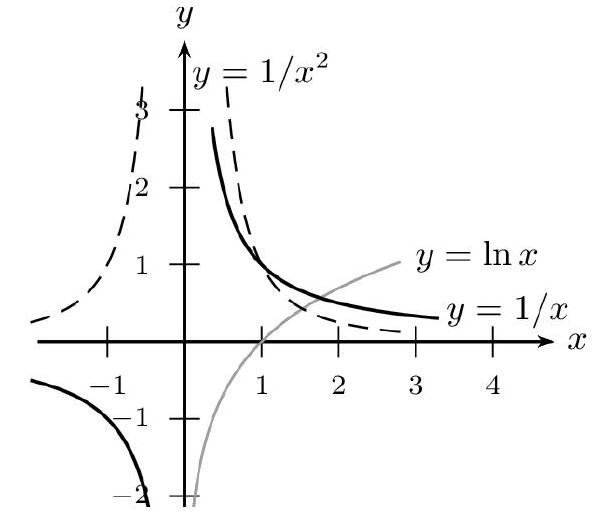
Limites de référence
$\lim _{\substack{x \rightarrow 0 \ x>0}} \frac{1}{x}=+\infty$ $\lim _{\substack{x \rightarrow 0 \ x<0}} \frac{1}{x}=-\infty$ $\lim _{x \rightarrow 0} \frac{1}{x^{2}}=+\infty$
Fonction vue en terminale
$\lim _{x \rightarrow 0} \ln x=-\infty$
Limite finie en un nombre réel $a$
La fonction $f$ a pour limite $l$ en a lorsque tout intervalle ouvert contenant $l$ contient toutes les valeurs de $f(x)$ pour $x$ assez «proche» de $a$. On note $\lim _{x \rightarrow a} f(x)=l$.
Cette définition permet de définir d'une part la continuité, d'autre part le nombre dérivé : $f^{\prime}(a)=\lim _{x \rightarrow a} \frac{f(x)-f(a)}{x-a}=\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}$
Limites de référence
Elles s'obtiennent en appliquant la définition du nombre dérivé ci-dessus (dérivée en 0 des fonctions $e^{x}, \ln (1+x)$ et $\sin x$ ). $\lim _{\substack{x \rightarrow 0 \ x \neq 0}} \frac{e^{x}-1}{x}=1$
Fonctions vue en terminale
$$ \lim _{\substack{x \rightarrow 0 \ x \neq 0}} \frac{\ln (1+x)}{x}=1 \quad \lim _{\substack{x \rightarrow 0 \ x \neq 0}} \frac{\sin x}{x}=1 $$
Unicité
Si elle existe, la limite d'une fonction en $a$ est unique.
III Opérations et composées
Opérations
La détermination de la limite d'une somme, d'un produit ou d'un quotient de 2 fonctions est intuitive, et vérifie les tableaux ci-dessous. Dans ces tableaux, a représente soit $+\infty$, soit $-\infty$, soit un nombre réel fixé. Retenir essentiellement les formes indéterminées (notées FI), à traiter cas par cas (voir exemples). Les méthodes utilisées pour déterminer les limites de suites se transposent aisément aux fonctions.
| $\lim _{x \rightarrow a} f(x)$ | 1 | 1 | 1 | $+\infty$ | $+\infty$ | $-\infty$ |
|---|---|---|---|---|---|---|
| $\lim _{x \rightarrow a} g(x)$ | 1, | $+\infty$ | $-\infty$ | $+\infty$ | $-\infty$ | $-\infty$ |
| $\lim _{x \rightarrow a}(f(x)+g(x))$ | $1+1^{\prime}$ | $+\infty$ | $-\infty$ | $+\infty$ | FI | $-\infty$ |
| $\lim _{x \rightarrow a} f(x)$ | 1 | $\mathrm{l}>0$ | $1>0$ | l<0 | l<0 | $+\infty$ | $+\infty$ | $-\infty$ | 0 |
|---|---|---|---|---|---|---|---|---|---|
| $\lim _{x \rightarrow a} g(x)$ | l' | $+\infty$ | $-\infty$ | $+\infty$ | $-\infty$ | $+\infty$ | $-\infty$ | $-\infty$ | $+\infty$ ou $-\infty$ |
| $\lim _{x \rightarrow a}(f(x) g(x))$ | ll' | $+\infty$ | $-\infty$ | $-\infty$ | $+\infty$ | $+\infty$ | $-\infty$ | $+\infty$ | FI |
| $\lim _{x \rightarrow a} f(x)$ | 1 | 1 | $+\infty$ | $+\infty$ | $-\infty$ | $-\infty$ | $+\infty$ ou $-\infty$ |
|---|---|---|---|---|---|---|---|
| $\lim _{x \rightarrow a} g(x)$ | $l^{\prime} \neq 0$ | $+\infty$ ou $-\infty$ | $l^{\prime}>0$ | $l^{\prime}<0$ | $l^{\prime}>0$ | $l^{\prime}<0$ | $+\infty$ ou $-\infty$ |
| $\lim _{x \rightarrow a} \frac{f(x)}{g(x)}$ | $\frac{l}{l^{\prime}}$ | 0 | $+\infty$ | $-\infty$ | $-\infty$ | $+\infty$ | FI |
| $\lim _{x \rightarrow a} f(x)$ | $l>0$ ou $+\infty$ | $l<0$ ou $-\infty$ | $l>0$ ou $+\infty$ | $l<0$ ou $-\infty$ | 0 |
|---|---|---|---|---|---|
| $\lim _{x \rightarrow a} g(x)$ | 0 et $g(x)>0$ | 0 et $g(x)>0$ | 0 et $g(x)<0$ | 0 et $g(x)<0$ | 0 |
| $\lim _{x \rightarrow a} \frac{f(x)}{g(x)}$ | $+\infty$ | $-\infty$ | $-\infty$ | $+\infty$ | FI |
Savoir faire
En cas de forme indéterminée dans une recherche de limite, il est souvent opportun de factoriser le terme «dominant » (celui qui impose la limite), même si la factorisation est artificielle.
Composée
$a, b$ et $c$ désignent $+\infty$, ou $-\infty$, ou un nombre réel $a$. Si $\lim _{x \rightarrow a} f(x)=b \quad$ et $\quad$ si $\lim _{y \rightarrow b} g(y)=c$, alors $\lim _{x \rightarrow a} g(f(x))=c$.
IV Comparaisons
Théorème de comparaison
Si $\lim _{x \rightarrow+\infty} f(x)=+\infty \quad$ et $\quad$ si, pour $x$ assez grand, $g(x) \geq f(x)$, alors $\lim _{x \rightarrow+\infty} g(x)=+\infty$.
Si $\lim _{x \rightarrow+\infty} f(x)=-\infty \quad$ et $\quad$ si, pour $x$ assez grand, $g(x) \leq f(x)$, alors $\lim _{x \rightarrow+\infty} g(x)=-\infty$.
Ces deux propriétés s'étendent facilement pour des limites en $-\infty$ ou en un réel $a$.
Théorème des gendarmes
Si $\lim _{x \rightarrow+\infty} f(x)=l \quad$ et $\quad$ si $\lim _{x \rightarrow+\infty} h(x)=l \quad$ et si, pour $x$ assez grand, $f(x) \leq g(x) \leq h(x)$, alors $\lim _{x \rightarrow+\infty} g(x)=l$.
Cette propriété s'étend facilement pour des limites en $-\infty$ ou en un réel $a$.
Exercices corrigés
Exercice 1
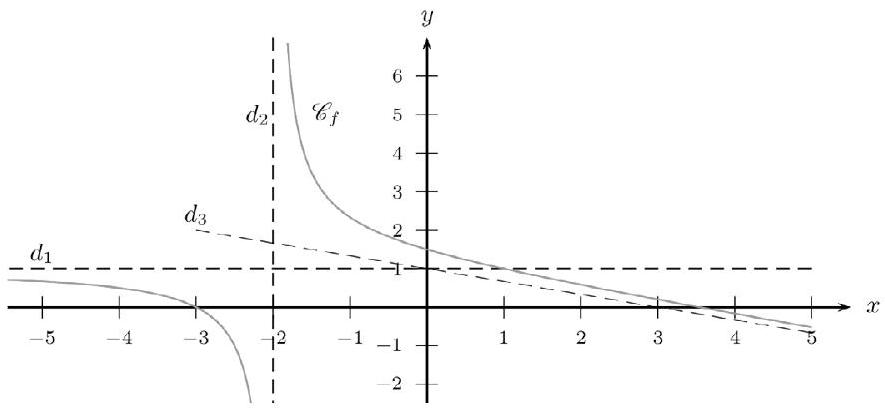
Un exercice graphique à savoir faire absolument.
- Conjecturer la valeur de $\lim _{x \rightarrow+\infty} f(x)$.
- Conjecturer la valeur chacune des limites suivantes, et donner, s'il y a lieu, l'équation réduite de l'asymptote associée.
$\lim _{x \rightarrow-\infty} f(x)$
$\lim _{x \rightarrow-2} f(x)$
$x<-2$
$\lim _{x \rightarrow-2} f(x)$
$x>-2$
Corrigé
- Comme $x$ tend vers $+\infty$, on considère un point $M$ sur la partie droite de $\mathrm{C}_{f}$, et on déplace $M$ vers la droite. On regarde vers quoi tend l'ordonnée de $M$. On conjecture que $\lim _{x \rightarrow+\infty} f(x)=-\infty$.
- Comme $x$ tend vers $-\infty$, on considère un point $M$ sur la partie gauche de $\mathrm{C}_{f}$, et on déplace $M$ vers la gauche. On regarde vers quoi tend l'ordonnée de $M$. On conjecture que $\lim {x \rightarrow-\infty} f(x)=1$. Donc la droite d'équation $y=1$ est asymptote horizontale à $\mathrm{C}{f}$.
Comme $x$ tend vers -2 en restant inférieur à -2 , on considère un point $M$ sur la partie gauche de $\mathrm{C}_{f}$, et on déplace $M$ vers la droite. On regarde vers quoi tend l'ordonnée de M.
On conjecture que $\lim {\substack{x \rightarrow-2 \ x<-2}} f(x)=-\infty$. Donc la droite d'équation $x=-2$ est asymptote verticale à $\mathrm{C}{f}$.
Comme $x$ tend vers -2 en restant supérieur à -2 , on considère un point $M$ sur la partie droite de $\mathrm{C}_{f}$, et on déplace $M$ vers la gauche. On regarde vers quoi tend l'ordonnée de M. On conjecture que $\lim _{x \rightarrow-2} f(x)=+\infty$.
$$ x>-2 $$
Donc la droite d'équation $x=-2$ est asymptote verticale à $\mathrm{C}_{f}$.
Exercice 2
Un exercice classique sur les calculs de limites.
- Soit $f$ la fonction définie par $f(x)=x^{2}+x+\frac{19}{x}$ pour tout réel $x$ non nul.
Déterminer $\lim _{x \rightarrow+\infty} f(x)$ et $\lim _{x \rightarrow-\infty} f(x)$. 2. Soit $f$ la fonction définie par $f(x)=\frac{x-1}{x^{2}+7}+5$ pour tout réel $x$.
Déterminer $\lim {x \rightarrow+\infty} f(x)$. En déduire une éventuelle asymptote de la courbe $\mathrm{C}{f}$. 3. Soit $f$ la fonction définie par $f(x)=\sqrt{x^{2}-x+9}$ pour tout réel $x$.
Déterminer $\lim _{x \rightarrow+\infty} f(x)$.
Corrigé
- $f(x)=x^{2}+x+\frac{19}{x}$.
Comme $\lim _{x \rightarrow+\infty} x^{2}=+\infty, \lim _{x \rightarrow+\infty} x=+\infty$, et $\lim _{x \rightarrow+\infty} \frac{19}{x}=0$, on obtient: $\lim _{x \rightarrow+\infty} f(x)=+\infty$ (limite d'une somme).
On obtient facilement $\lim _{x \rightarrow-\infty} x^{2}=+\infty$ et $\lim _{x \rightarrow-\infty} x=-\infty$, ce qui conduit à une forme indéterminée. On factorise alors le terme «dominant» de la somme $x^{2}+x$. On a : $x^{2}+x=x^{2}\left(1+\frac{1}{x}\right)$. Or $\lim _{x \rightarrow-\infty} x^{2}=+\infty$, et $\lim _{x \rightarrow-\infty} 1+\frac{1}{x}=1+0=1$. Donc $\lim _{x \rightarrow-\infty} x^{2}+x=+\infty$ (limite d'un produit).
Par ailleurs $\lim _{x \rightarrow-\infty} \frac{19}{x}=0$. Donc $\lim _{x \rightarrow-\infty} f(x)=+\infty$ (limite d'une somme). 2. $f(x)=\frac{x-1}{x^{2}+7}+5$.
On obtient facilement $\lim _{x \rightarrow+\infty} x-1=+\infty$ et $\lim _{x \rightarrow+\infty} x^{2}+7=+\infty$, ce qui conduit à une forme indéterminée. On factorise alors les termes «dominants» du quotient et on simplifie. $f(x)=\frac{x\left(1-\frac{1}{x}\right)}{x^{2}\left(1+\frac{7}{x^{2}}\right)}+5=\frac{1}{x} \frac{1-\frac{1}{x}}{1+\frac{7}{x^{2}}}+5$. $\lim {x \rightarrow+\infty} f(x)=0 \times \frac{1-0}{1+0}+5=5$ (opérations sur les limites). Donc la droite horizontale d'équation $y=5$ est une asymptote de la courbe $\mathrm{C}{f}$ en $+\infty$. 3. $f(x)=\sqrt{x^{2}-x+9}$.
On obtient facilement $\lim _{x \rightarrow+\infty} x^{2}=+\infty$ et $\lim _{x \rightarrow+\infty}-x=-\infty$, ce qui conduit à une forme indéterminée. On factorise alors le terme «dominant» de la somme $x^{2}-x+9$. $x^{2}-x+9=x^{2}\left(1-\frac{1}{x}+\frac{9}{x^{2}}\right)$. Comme $\lim _{x \rightarrow+\infty} x^{2}=+\infty$ et $\lim _{x \rightarrow+\infty} 1-\frac{1}{x}+\frac{9}{x^{2}}=1-0+0=1$, on obtient: $\lim _{x \rightarrow+\infty} x^{2}-x+9=+\infty$. Or : $\lim _{y \rightarrow+\infty} \sqrt{y}=+\infty$. Donc : $\lim _{x \rightarrow+\infty} f(x)=+\infty$ (limite d'une composée).
Exercice 3
Un exercice classique sur les calculs de limites.
- Soit $g$ la fonction définie par $g(x)=\frac{8}{1+2 e^{-0,04 x}}$ pour tout réel $x$.
Déterminer $\lim _{x \rightarrow+\infty} g(x)$ et $\lim _{x \rightarrow-\infty} g(x)$. 2. Soit $f$ la fonction définie par $f(x)=(x+1) e^{x}$ pour tout réel $x$.
Déterminer $\lim _{x \rightarrow+\infty} f(x)$ et $\lim {x \rightarrow-\infty} f(x)$. En déduire les éventuelles asymptotes de la courbe $\mathrm{C}{f}$. 3. Soit $f$ la fonction définie par $f(x)=(x+2) e^{-x}$ pour tout réel $x$.
Déterminer $\lim _{x \rightarrow+\infty} f(x)$ et $\lim {x \rightarrow-\infty} f(x)$. En déduire les éventuelles asymptotes de la courbe $\mathrm{C}{f}$. 4. Soit $f$ la fonction définie par $f(x)=3 x e^{-\frac{1}{4} x}+5$ pour tout réel $x$.
Déterminer $\lim _{x \rightarrow+\infty} f(x)$. Interpréter le résultat.
Corrigé
- $g(x)=\frac{8}{1+2 e^{-0,04 x}}$
Comme $\lim _{x \rightarrow+\infty}-0,04 x=-\infty$ et $\lim _{y \rightarrow-\infty} e^{y}=0$, on obtient $\lim _{x \rightarrow+\infty} e^{-0,04 x}=0$ (limite d'une composée). D'où $\lim _{x \rightarrow+\infty} g(x)=\frac{8}{1+2 \times 0}=8$.
Comme $\lim _{x \rightarrow-\infty}-0,04 x=+\infty$ et $\lim _{y \rightarrow+\infty} e^{y}=+\infty$, on obtient $\lim _{x \rightarrow+\infty} e^{-0,04 x}=+\infty$ (limite d'une composée). D'où $\lim _{x \rightarrow+\infty} 1+2 e^{-0,04 x}=+\infty$. Et par là $\lim _{x \rightarrow-\infty} g(x)=0$ (limite d'un quotient). 2. $f(x)=(x+1) e^{x}$.
Comme $\lim _{x \rightarrow+\infty} x+1=+\infty$ et $\lim _{x \rightarrow+\infty} e^{x}=+\infty$, on obtient $\lim _{x \rightarrow+\infty} f(x)=+\infty$.
On obtient facilement $\lim _{x \rightarrow-\infty} x+1=-\infty$ et $\lim _{x \rightarrow-\infty} e^{x}=0$, ce qui conduit à une forme indéterminée. On développe alors le produit $f(x)$. $f(x)=x e^{x}+e^{x}$. Comme $\lim _{x \rightarrow-\infty} x e^{x}=0$ et $\lim _{x \rightarrow-\infty} e^{x}=0$, on obtient $\lim {x \rightarrow-\infty} f(x)=0$ (limite d'une somme). Donc la droite horizontale d'équation $y=0$ (l'axe des abscisses) est une asymptote de la courbe $\mathrm{C}{f}$ en $-\infty$. 3. $f(x)=(x+2) e^{-x}$.
Comme $\lim _{x \rightarrow+\infty}-x=-\infty$ et $\lim _{y \rightarrow-\infty} e^{y}=0$, on obtient $\lim _{x \rightarrow+\infty} e^{-x}=0$.
On obtient facilement $\lim _{x \rightarrow+\infty} x+2=+\infty$. Comme $\lim _{x \rightarrow+\infty} e^{-x}=0$, cela conduit à une forme indéterminée. On développe alors le produit $f(x)$. $f(x)=x e^{-x}+2 e^{-x}=-\left(-x e^{-x}\right)+2 e^{-x}$. Comme $\lim _{x \rightarrow+\infty}-x=-\infty$ et $\lim _{y \rightarrow-\infty} y e^{y}=0$, on obtient $\lim _{x \rightarrow+\infty}-x e^{-x}=0$. Donc $\lim {x \rightarrow+\infty} f(x)=-0+2 \times 0=0$. Donc la droite horizontale d'équation $y=0$ (l'axe des abscisses) est une asymptote de la courbe $\mathrm{C}{f}$ en $+\infty$.
Comme $\lim _{x \rightarrow-\infty}-x=+\infty$ et $\lim _{y \rightarrow+\infty} e^{y}=+\infty$, on obtient $\lim _{x \rightarrow-\infty} e^{-x}=+\infty$. Par ailleurs : $\lim _{x \rightarrow-\infty} x+2=-\infty$. D'où : $\lim _{x \rightarrow-\infty} f(x)=-\infty$ (limite d'un produit). 4. $f(x)=3 x e^{-\frac{1}{4} x}+5$.
Comme $\lim _{x \rightarrow+\infty}-\frac{1}{4} x=-\infty$ et $\lim _{y \rightarrow-\infty} e^{y}=0$, on obtient $\lim _{x \rightarrow+\infty} e^{-\frac{1}{4} x}=0$. Mais comme $\lim _{x \rightarrow+\infty} 3 x=+\infty$, cela conduit à une forme indéterminée. On fait apparaître $-\frac{1}{4} x$ devant l'exponentielle pour utiliser la limite de $y e^{y}$ en $-\infty$. On a: $f(x)=-12 \times-\frac{1}{4} x e^{-\frac{1}{4} x}+5$. Comme $\lim _{x \rightarrow+\infty}-\frac{1}{4} x=-\infty$ et $\lim _{y \rightarrow-\infty} y e^{y}=0$, on obtient $\lim _{x \rightarrow+\infty}-\frac{1}{4} x e^{-\frac{1}{4} x}=0$. Par conséquent : $\lim {x \rightarrow+\infty} f(x)=-12 \times 0+5=5$. Donc la droite horizontale d'équation $y=5$ est une asymptote de la courbe $\mathrm{C}{f}$ en $+\infty$.
Exercice 4
Un exercice classique sur les calculs de limites.
Attention! Cet exercice utilise la fonction logarithme népérien.
- Soit $h$ la fonction définie par $h(x)=\frac{1+\ln x}{x^{2}}$ sur $] 0 ;+\infty[$.
Déterminer $\lim _{x \rightarrow 0} h(x)$ et $\lim _{x \rightarrow+\infty} h(x)$. 2. Soit $f$ la fonction définie par $f(x)=\frac{1+2 \ln x}{x}$ sur $] 0 ;+\infty[$.
Déterminer $\lim _{x \rightarrow 0} f(x)$ et $\lim {x \rightarrow+\infty} f(x)$. En déduire les éventuelles asymptotes de la courbe $\mathrm{C}{f}$.
Corrigé
- $h(x)=\frac{1+\ln x}{x^{2}}$.
On a: $\lim _{x \rightarrow 0} \ln x=-\infty$, et donc : $\lim _{x \rightarrow 0} 1+\ln x=-\infty$. Par ailleurs: $\lim _{x \rightarrow 0} x^{2}=0$ et $x^{2}$ reste strictement positif. Donc $\lim _{x \rightarrow 0} h(x)=-\infty$ (limite d'un quotient).
On obtient facilement $\lim _{x \rightarrow+\infty} 1+\ln x=+\infty$ et $\lim _{x \rightarrow+\infty} x^{2}=+\infty$, ce qui conduit à une forme indéterminée. On factorise alors le terme dominant du numérateur. $h(x)=\frac{\ln x}{x} \frac{1+\frac{1}{\ln x}}{x}$. Examinons le facteur de gauche. On a : $\lim _{x \rightarrow+\infty} \frac{\ln x}{x}=0$. Examinons le facteur de droite. Tout d'abord : $\lim _{x \rightarrow+\infty} 1+\frac{1}{\ln x}=1+0=1$. Et donc, comme $\lim _{x \rightarrow+\infty} x=+\infty$, on obtient : $\lim _{x \rightarrow+\infty} \frac{1+\frac{1}{\ln x}}{x}=0$. Donc, finalement : $\lim _{x \rightarrow+\infty} h(x)=0 \times 0=0$ (limite d'un produit) 2. $f(x)=\frac{1+2 \ln x}{x}$.
On a: $\lim _{x \rightarrow 0} \ln x=-\infty$, et donc : $\lim _{x \rightarrow 0} 1+2 \ln x=-\infty$. Par ailleurs : $\lim _{x \rightarrow 0} x=0$ et $x$ reste strictement positif (sur $] 0 ;+\infty[$ ). Donc $\lim {x \rightarrow 0} h(x)=-\infty$ (limite d'un quotient). Donc la droite verticale d'équation $x=0$ (l'axe des ordonnées) est une asymptote de la courbe $\mathrm{C}{f}$ en 0 .
On obtient facilement $\lim _{x \rightarrow+\infty} 1+2 \ln x=+\infty$ et $\lim _{x \rightarrow+\infty} x=+\infty$, ce qui conduit à une forme indéterminée. On factorise alors le terme dominant du numérateur. $h(x)=\frac{\ln x}{x}\left(1+\frac{1}{\ln x}\right)$. Examinons le facteur de gauche. On a : $\lim _{x \rightarrow+\infty} \frac{\ln x}{x}=0$. Examinons le facteur de droite. $\lim _{x \rightarrow+\infty} 1+\frac{1}{\ln x}=1+0=1$. Donc, finalement: $\lim {x \rightarrow+\infty} h(x)=0 \times 0=0$ (limite d'un produit). Donc la droite horizontale d'équation $y=0$ (l'axe des abscisses) est une asymptote de la courbe $\mathrm{C}{f}$ en $+\infty$.
Exercice 5
Un exercice sur les limites utilisant des fonctions circulaires.
- Soit $g$ la fonction définie par $g(x)=x^{2}-\frac{\cos x}{x}$ sur $\left.I=\right] 0 ;+\infty[$.
Déterminer par comparaison $\lim _{x \rightarrow+\infty} g(x)$. 2. Soit $h$ la fonction définie par $h(x)=\frac{1}{x \cos x}$ sur $\left.\left.I=\right] 0 ; \frac{\pi}{4}\right]$.
Déterminer par comparaison $\lim _{x \rightarrow 0} h(x)$.
Corrigé
L'expression «par comparaison» signifie qu'il faut utiliser le théorème de comparaison ou le théorème des gendarmes.
- Pour tout réel $x$, on a : $-1 \leq \cos x \leq 1$, et par là : $\frac{-1}{x} \leq \frac{\cos x}{x} \leq \frac{1}{x}$.
Le sens des inégalités n'a pas changé car $x$ est strictement positif. Or, comme $\lim _{x \rightarrow+\infty} \frac{-1}{x}=0$ et $\lim _{x \rightarrow+\infty} \frac{1}{x}=0$, on obtient, d'après le théorème des gendarmes : $\lim _{x \rightarrow+\infty} \frac{\cos x}{x}=0$. Par ailleurs, on a : $\lim _{x \rightarrow+\infty} x^{2}=+\infty$. Donc, finalement, on obtient $\lim _{x \rightarrow+\infty} g(x)=+\infty$ (limite d'une somme). 2. Pour tout réel $x$ dans $\left.] 0 ; \frac{\pi}{4}\right]$, on a : $\cos 0 \geq \cos x \geq \frac{\pi}{4}$ (car la fonction cosinus est décroissante sur cet intervalle). Soit: $1 \geq \cos x \geq \frac{\sqrt{2}}{2}$.
Et par là : $x \geq x \cos x \geq x \frac{\sqrt{2}}{2}$. Le sens des inégalités n'a pas changé car $x$ est strictement positif. Et finalement: $\frac{1}{x} \leq \frac{1}{x \cos x} \leq \frac{1}{x} \frac{2}{\sqrt{2}}$ (le sens des inégalités a changé car la fonction inverse est décroissante sur $\mathbb{R}_{+}^{*}$ ). On obtient en particulier : $\frac{1}{x} \leq \frac{1}{x \cos x}$. Or : $\lim _{x \rightarrow 0} \frac{1}{x}=+\infty(\operatorname{car} x$ reste strictement positif dans $I)$. On obtient donc, par comparaison : $\lim _{x \rightarrow 0} h(x)=+\infty$.
