Cours : Limites de fonctions

Limites de fonctions

I Limites en $+\infty$ ou en $-\infty$

Limite infinie en $+\infty$ ou en $-\infty$

La fonction $f$ a pour limite $+\infty$ en $+\infty$ lorsque tout intervalle du type $] A ;+\infty[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$ pour $x$ assez «grand». On note $\lim _{x \rightarrow+\infty} f(x)=+\infty$.

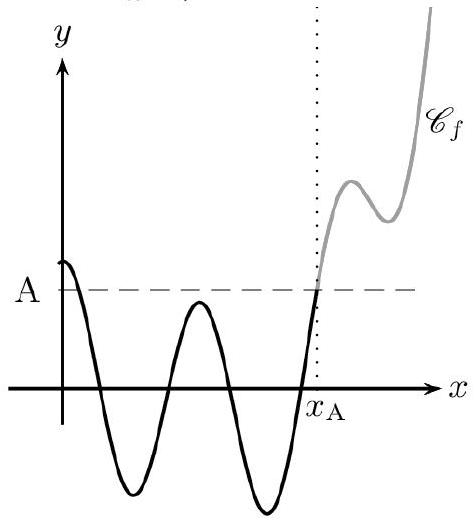
La fonction $f$ a pour limite $-\infty$ en $+\infty$ lorsque tout intervalle du type $]-\infty$; $A$ [ (où $A$ est un réel) contient toutes les valeurs de $f(x)$ pour $x$ assez «grand». On note $\lim _{x \rightarrow+\infty} f(x)=-\infty$.

La fonction $f$ a pour limite $+\infty$ en $-\infty$ lorsque tout intervalle du type $] A ;+\infty[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$ pour $x$ assez «négatif». On note $\lim _{x \rightarrow-\infty} f(x)=+\infty$.

La fonction $f$ a pour limite $-\infty$ en $-\infty$ lorsque tout intervalle du type $]-\infty$; $A$ [ (où $A$ est un réel) contient toutes les valeurs de $f(x)$ pour $x$ assez « négatif». On note $\lim _{x \rightarrow-\infty} f(x)=-\infty$.

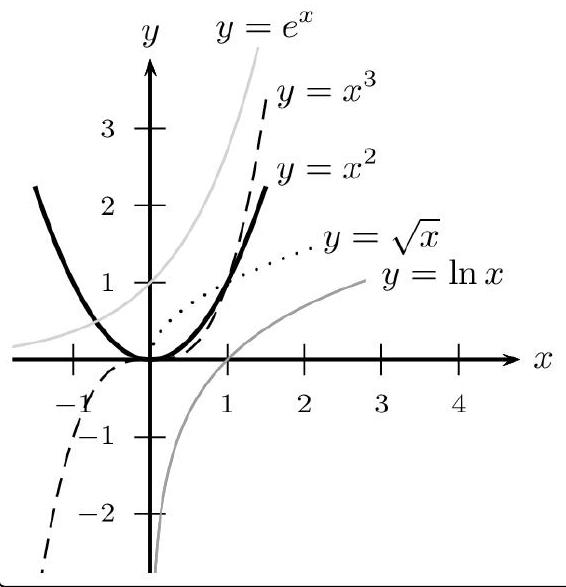
Limites de référence

$\lim _{x \rightarrow+\infty} x=+\infty \quad \lim _{x \rightarrow+\infty} x^{2}=+\infty \quad \lim _{x \rightarrow+\infty} x^{n}=+\infty \quad($ pour $n \in \mathbb{N}$ et $n>0)$

$$ \left\lvert, \begin{aligned} & \lim _{x \rightarrow+\infty} \sqrt{x}=+\infty \ & \lim _{x \rightarrow-\infty} x=-\infty \quad \lim _{x \rightarrow-\infty} x^{2}=+\infty \quad \lim _{x \rightarrow-\infty} x^{3}=-\infty \ & \lim _{x \rightarrow+\infty} e^{x}=+\infty \quad \lim _{x \rightarrow+\infty} \frac{e^{x}}{x}=+\infty \quad \lim _{x \rightarrow+\infty} \frac{e^{x}}{x^{n}}=+\infty(\text { pour } n \in \mathbb{N}) \end{aligned}\right. $$

Fonction vue en terminale

$\lim _{x \rightarrow+\infty} \ln x=+\infty$

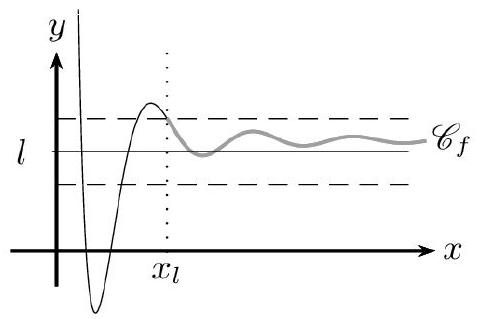
Limite finie en $+\infty$ ou en $-\infty$

La fonction $f$ a pour limite $l$ en $+\infty$ lorsque tout intervalle ouvert contenant $l$ contient toutes les valeurs de $f(x)$ pour $x$ assez «grand». On note $\lim _{x \rightarrow+\infty} f(x)=l$. On dit que, dans un repère, la droite $d$ d'équation $y=l$ est asymptote horizontale en $+\infty$ à la courbe représentative C de $f$.

La fonction $f$ a pour limite $l$ en $-\infty$ lorsque tout intervalle ouvert contenant $l$ contient toutes les valeurs $f(x)$ pour $x$ assez « négatif». On note $\lim _{x \rightarrow-\infty} f(x)=l$.

On dit que, dans un repère, la droite $d$ d'équation $y=l$ est asymptote horizontale en $-\infty$ à la courbe représentative C de $f$.

Fonction constante

Soit $l$ un nombre réel; si $f(x)=l$, alors $\lim _{x \rightarrow+\infty} f(x)=\lim _{x \rightarrow-\infty} f(x)=l$.

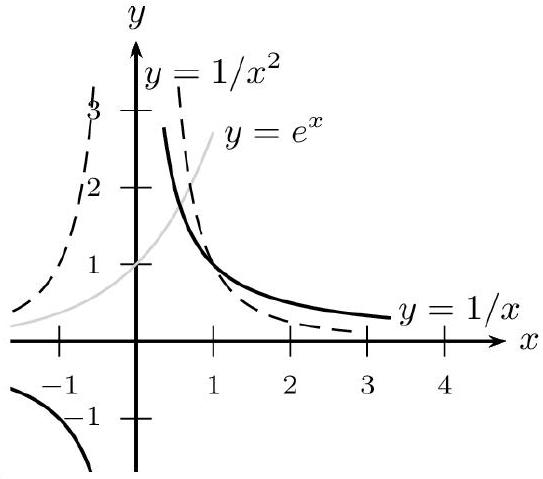
Limites de référence

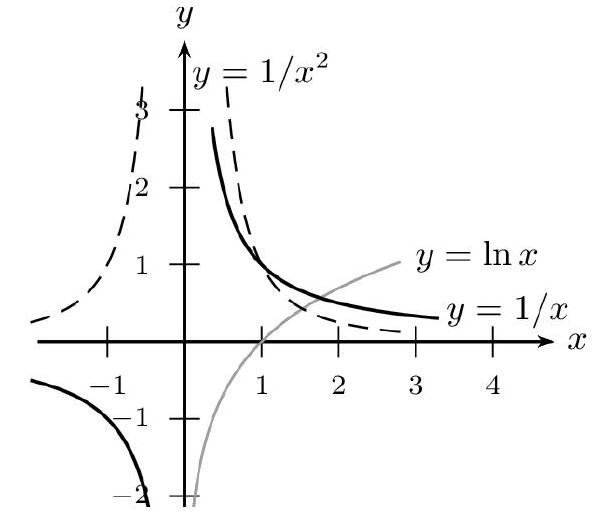
$\lim _{x \rightarrow+\infty} \frac{1}{x}=\lim _{x \rightarrow-\infty} \frac{1}{x}=0 \quad \lim _{x \rightarrow+\infty} \frac{1}{x^{2}}=\lim _{x \rightarrow-\infty} \frac{1}{x^{2}}=0$ $\lim _{x \rightarrow+\infty} \frac{1}{x^{n}}=\lim _{x \rightarrow-\infty} \frac{1}{x^{n}}=0(\operatorname{pour} n \in \mathbb{N}$ et $n>0) \quad \lim _{x \rightarrow+\infty} \frac{1}{\sqrt{x}}=0$ $\lim _{x \rightarrow-\infty} e^{x}=0 \quad \lim _{x \rightarrow-\infty} x e^{x}=0 \quad \lim _{x \rightarrow-\infty} x^{n} e^{x}=0($ pour $n \in \mathbb{N})$

Fonction vue en terminale

$\lim _{x \rightarrow+\infty} \frac{\ln x}{x}=0$

Unicité

Si elle existe, la limite d'une fonction en l'infini est unique.

II Limites en a

Limite infinie en un nombre réel $\boldsymbol{a}$

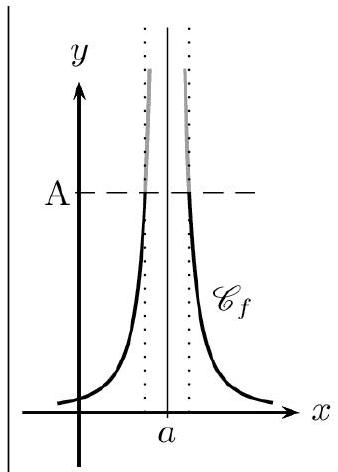
La fonction $f$ a pour limite $+\infty$ en a lorsque tout intervalle du type $] A ;+\infty[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$ pour $x$ assez «proche» de $a$. On note : $\lim _{x \rightarrow a} f(x)=+\infty$.

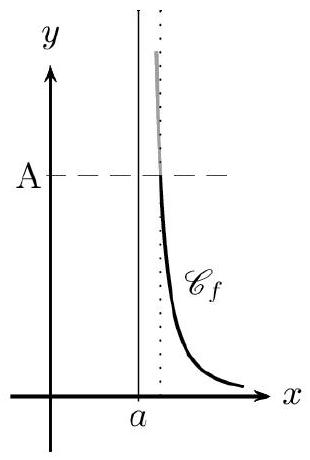
La fonction $f$ a pour limite $+\infty$ à droite en a lorsque tout intervalle du type $] A ;+\infty[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$ pour $x$ assez «proche» de $a$ tout en restant supérieur à $a$. On note : $\lim _{\substack{x \rightarrow a \ x>a}} f(x)=+\infty$.

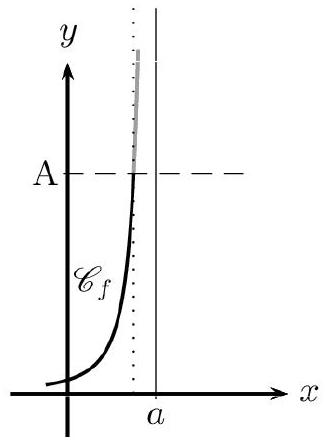
La fonction $f$ a pour limite $+\infty$ à gauche en $a$ lorsque tout intervalle du type $] A ;+\infty[$ (où $A$ est un réel) contient toutes les valeurs de $f(x)$ pour $x$ assez «proche» de $a$ en restant inférieur à $a$. On note : $\lim _{\substack{x \rightarrow a \ x<a}} f(x)=+\infty$.

On définit de façon analogue une limite $-\infty$ en $a$, à droite en $a$, ou à gauche en $a$.

Dans tous les cas précédents, on dit que, dans un repère, la droite $d$ d'équation $x=a$ est asymptote verticale en $a$ à la courbe représentative C de $f$.

Limites de référence

$\lim _{\substack{x \rightarrow 0 \ x>0}} \frac{1}{x}=+\infty$ $\lim _{\substack{x \rightarrow 0 \ x<0}} \frac{1}{x}=-\infty$ $\lim _{x \rightarrow 0} \frac{1}{x^{2}}=+\infty$

Fonction vue en terminale

$\lim _{x \rightarrow 0} \ln x=-\infty$

Limite finie en un nombre réel $a$

La fonction $f$ a pour limite $l$ en a lorsque tout intervalle ouvert contenant $l$ contient toutes les valeurs de $f(x)$ pour $x$ assez «proche» de $a$. On note $\lim _{x \rightarrow a} f(x)=l$.

Cette définition permet de définir d'une part la continuité, d'autre part le nombre dérivé : $f^{\prime}(a)=\lim _{x \rightarrow a} \frac{f(x)-f(a)}{x-a}=\lim _{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}$

Limites de référence

Elles s'obtiennent en appliquant la définition du nombre dérivé ci-dessus (dérivée en 0 des fonctions $e^{x}, \ln (1+x)$ et $\sin x$ ). $\lim _{\substack{x \rightarrow 0 \ x \neq 0}} \frac{e^{x}-1}{x}=1$

Fonctions vue en terminale

$$ \lim _{\substack{x \rightarrow 0 \ x \neq 0}} \frac{\ln (1+x)}{x}=1 \quad \lim _{\substack{x \rightarrow 0 \ x \neq 0}} \frac{\sin x}{x}=1 $$

Unicité

Si elle existe, la limite d'une fonction en $a$ est unique.

III Opérations et composées

Opérations

La détermination de la limite d'une somme, d'un produit ou d'un quotient de 2 fonctions est intuitive, et vérifie les tableaux ci-dessous. Dans ces tableaux, a représente soit $+\infty$, soit $-\infty$, soit un nombre réel fixé. Retenir essentiellement les formes indéterminées (notées FI), à traiter cas par cas (voir exemples). Les méthodes utilisées pour déterminer les limites de suites se transposent aisément aux fonctions.

$\lim _{x \rightarrow a} f(x)$	1	1	1	$+\infty$	$+\infty$	$-\infty$
$\lim _{x \rightarrow a} g(x)$	1,	$+\infty$	$-\infty$	$+\infty$	$-\infty$	$-\infty$
$\lim _{x \rightarrow a}(f(x)+g(x))$	$1+1^{\prime}$	$+\infty$	$-\infty$	$+\infty$	FI	$-\infty$

$\lim _{x \rightarrow a} f(x)$	1	$\mathrm{l}>0$	$1>0$	l<0	l<0	$+\infty$	$+\infty$	$-\infty$	0
$\lim _{x \rightarrow a} g(x)$	l'	$+\infty$	$-\infty$	$+\infty$	$-\infty$	$+\infty$	$-\infty$	$-\infty$	$+\infty$ ou $-\infty$
$\lim _{x \rightarrow a}(f(x) g(x))$	ll'	$+\infty$	$-\infty$	$-\infty$	$+\infty$	$+\infty$	$-\infty$	$+\infty$	FI

$\lim _{x \rightarrow a} f(x)$	1	1	$+\infty$	$+\infty$	$-\infty$	$-\infty$	$+\infty$ ou $-\infty$
$\lim _{x \rightarrow a} g(x)$	$l^{\prime} \neq 0$	$+\infty$ ou $-\infty$	$l^{\prime}>0$	$l^{\prime}<0$	$l^{\prime}>0$	$l^{\prime}<0$	$+\infty$ ou $-\infty$
$\lim _{x \rightarrow a} \frac{f(x)}{g(x)}$	$\frac{l}{l^{\prime}}$	0	$+\infty$	$-\infty$	$-\infty$	$+\infty$	FI

$\lim _{x \rightarrow a} f(x)$	$l>0$ ou $+\infty$	$l<0$ ou $-\infty$	$l>0$ ou $+\infty$	$l<0$ ou $-\infty$	0
$\lim _{x \rightarrow a} g(x)$	0 et $g(x)>0$	0 et $g(x)>0$	0 et $g(x)<0$	0 et $g(x)<0$	0
$\lim _{x \rightarrow a} \frac{f(x)}{g(x)}$	$+\infty$	$-\infty$	$-\infty$	$+\infty$	FI

Savoir faire

En cas de forme indéterminée dans une recherche de limite, il est souvent opportun de factoriser le terme «dominant » (celui qui impose la limite), même si la factorisation est artificielle.

Composée

$a, b$ et $c$ désignent $+\infty$, ou $-\infty$, ou un nombre réel $a$. Si $\lim _{x \rightarrow a} f(x)=b \quad$ et $\quad$ si $\lim _{y \rightarrow b} g(y)=c$, alors $\lim _{x \rightarrow a} g(f(x))=c$.

IV Comparaisons

Théorème de comparaison

Si $\lim _{x \rightarrow+\infty} f(x)=+\infty \quad$ et $\quad$ si, pour $x$ assez grand, $g(x) \geq f(x)$, alors $\lim _{x \rightarrow+\infty} g(x)=+\infty$.

Si $\lim _{x \rightarrow+\infty} f(x)=-\infty \quad$ et $\quad$ si, pour $x$ assez grand, $g(x) \leq f(x)$, alors $\lim _{x \rightarrow+\infty} g(x)=-\infty$.

Ces deux propriétés s'étendent facilement pour des limites en $-\infty$ ou en un réel $a$.

Théorème des gendarmes

Si $\lim _{x \rightarrow+\infty} f(x)=l \quad$ et $\quad$ si $\lim _{x \rightarrow+\infty} h(x)=l \quad$ et si, pour $x$ assez grand, $f(x) \leq g(x) \leq h(x)$, alors $\lim _{x \rightarrow+\infty} g(x)=l$.

Cette propriété s'étend facilement pour des limites en $-\infty$ ou en un réel $a$.