Exercices : Succession d'épreuves indépendantes, schéma de Bernoulli

Exercices corrigés

Exercice 1

Un examen comporte 3 épreuves, $\mathrm{A}, \mathrm{B}$ et C . Un candidat quelconque passe cet examen. A : "le candidat a réussi l'épreuve A ". B : "le candidat a réussi l'épreuve B". C : "le candidat a réussi l'épreuve C ". On a déterminé statistiquement que : $p(A)=0,7$ et $p(B)=0,2$, mais on ne connaît pas $p(C)$. Le candidat est reçu à cet examen s'il a réussi au moins deux épreuves sur trois. Soit S : "le candidat a réussi l'examen". On sait que : $p(S)=0,388$. Déterminer $p(C)$.

Corrigé

Nous sommes en présence de 3 épreuves indépendantes. En posant $p(C)=p$, nous pouvons dresser l'arbre de probabilité suivant.

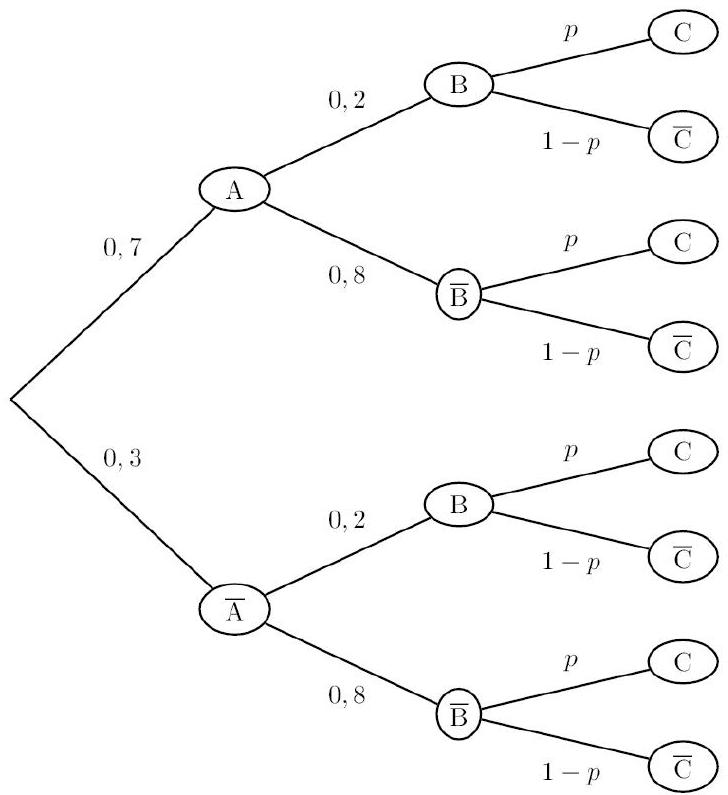
On a : $S={(A, B, C),(A, B, \bar{C}),(A, \bar{B}, C),(\bar{A}, B, C)}$. On obtient alors : $p(S)=p((A, B, C))+p((A, B, \bar{C}))+p((A, \bar{B}, C))+p((\bar{A}, B, C))$. $0,388=0,7 \times 0,2 \times p+0,7 \times 0,2 \times(1-p)+0,7 \times 0,8 \times p+0,3 \times 0,2 \times p$. Soit : $0,388=0,14 p+0,14-0,14 p+0,56 p+0,06 p$. Soit : $0,248=0,62 p$. Et par là : $p=0,4$.

Exercice 2

Partie A

Les 9 lettres du mot EXERCICES sont mises dans une urne. On tire au hasard 3 lettres de l'urne, successivement mais avec remise. On compte le nombre de voyelles obtenues.

1. Cette situation est-elle modélisée par un schéma de Bernoulli ?
2. Représenter la situation par un arbre pondéré.
3. Soit A: «aucune voyelle n'est piochée».

Soit B : «exactement une voyelle a été piochée». Soit C : «on a pioché plus de voyelles que de consonnes ». Déterminer les probabilités de ces 3 événements.

Partie B

Répondre aux mêmes questions que celles de la partie A dans le cas où les tirages sont sans remise.

Corrigé

Partie A

1. On répète 3 fois de manière indépendante une expérience à 2 issues :

V : «la lettre est une voyelle», C : « la lettre est une consonne». On a $p(V)=\frac{4}{9}$. Nous sommes donc en présence d'un schéma de Bernoulli de paramètres $n=3$ et $p=\frac{4}{9}$. 2. Voici un arbre pondéré convenable.

On notera que les mêmes probabilités $\frac{4}{9}$ et $\frac{5}{9}$ se répètent sur les couples de branches. 3. $p(A)=p((C, C, C))=(1-p)^{3}=\frac{125}{729} \approx 0,17$. $p(B)=p((V, C, C))+p((C, V, C))+p((C, C, V))=3 p(1-p)^{2}=\frac{100}{243} \approx 0,41$. $C=\overline{A \cup B}$ et A et B sont incompatibles. Donc $p(C)=1-(p(A)+p(B))=\frac{304}{729} \approx 0,42$.

Partie B

1. On répète 3 fois une expérience à 2 issues :

V : «la lettre est une voyelle», C: «la lettre est une consonne». Mais les tirages ne sont plus indépendants. Nous ne sommes donc pas en présence d'un schéma de Bernoulli. 2. Voici page suivante un arbre pondéré convenable.

On notera que les probabilités ne se répètent pas sur les couples de branches. Cela est évidemment dû au fait que les tirages ne sont pas indépendants. 3. $p(A)=p((C, C, C))=\frac{5}{9} \times \frac{4}{8} \times \frac{3}{7}=\frac{5}{42} \approx 0,12$. $p(B)=p((V, C, C))+p((C, V, C))+p((C, C, V))$. Soit : $p(B)=\frac{4}{9} \times \frac{5}{8} \times \frac{4}{7}+\frac{5}{9} \times \frac{4}{8} \times \frac{4}{7}+\frac{5}{9} \times \frac{4}{8} \times \frac{4}{7}=\frac{10}{21} \approx 0,48$. $C=\overline{A \cup B}$ et A et B sont incompatibles. Donc $p(C)=1-(p(A)+p(B))=\frac{17}{42} \approx 0,40$.

Exercice 3

Un virus a contaminé $1 %$ de la population. On considère un échantillon de 100 personnes. La population est suffisamment importante pour assimiler cet échantillon à un tirage aléatoire avec remise. On note $X$ la variable aléatoire qui comptabilise le nombre de malades dans l'échantillon.

1. Justifier que la variable aléatoire $X$ suit une loi binomiale dont on donnera les paramètres.
2. Déterminer la probabilité qu'il y ait exactement 5 malades dans l'échantillon. On arrondira le résultat au dix-millième.
3. Déterminer la probabilité qu'il y ait au moins 5 malades dans l'échantillon. On donnera une valeur arrondie au dix-millième.
4. Déterminer la probabilité que le nombre de malades dans l'échantillon soit dans l'intervalle [2;5]. On donnera une valeur arrondie au dix-millième.

Corrigé

1. Le choix de l'échantillon revient à répéter 100 fois de manière indépendante une expérience à 2 issues : S : «la personne est malade», E: «la personne n'est pas malade». On a $p(S)=0,01$, et X dénombre les «succès». On en déduit que $X$ suit une loi binomiale de paramètres $n=100$ et $p=0,01$.
2. À la calculatrice, on obtient : $p(X=5) \approx 0,0029$.
3. On cherche $p(X \geq 5)$.

Or $p(X \geq 5)=1-p(X<5)=1-p(X \leq 4)$. Et à la calculatrice, on obtient: $p(X \leq 4) \approx 0,9966$. Donc $p(X \geq 5) \approx 0,0034$. 4. On cherche $p(2 \leq X \leq 5)=p(X \leq 5)-p(X<2)=p(X \leq 5)-p(X \leq 1)$.

Et à la calculatrice, on obtient: $p(X \leq 5) \approx 0,9995$ et $p(X \leq 1) \approx 0,7358$. Donc $p(2 \leq X \leq 5) \approx 0,2637$.

Exercice 4

Un opérateur de téléphonie mobile organise une campagne de démarchage par téléphone pour proposer la souscription d'un nouveau forfait à sa clientèle, composée à 65% d'hommes.

Des études préalables ont montré que $30 %$ des hommes contactés écoutent les explications, les autres raccrochant aussitôt (ou se déclarant immédiatement non intéressés). Parmi les femmes, $60 %$ écoutent les explications. On admet que ces proportions restent stables.

Partie A

On choisit au hasard une personne dans le fichier clients. Chaque personne a la même probabilité d'être choisie. On note : H l'événement «la personne choisie est un homme», F l'événement «la personne choisie est une femme»,

E l'événement «la personne choisie écoute les explications du démarcheur». $\bar{E}$ est l'événement contraire de E .

1. Recopier et compléter l'arbre de probabilité ci-dessous. 2.a. Traduire par une phrase l'événement $E \cap F$ et calculer sa probabilité. 2.b. Montrer que la probabilité que la personne choisie écoute les explications du démarcheur est égale à 0,405 . 2.c. Le démarcheur s'adresse à une personne qui l'écoute.

Quelle est la probabilité que ce soit un homme ? On donnera le résultat arrondi au centième.

Partie B

Les relevés réalisés au cours de ces premières journées permettent également de constater que $12 %$ des personnes interrogées souscrivent à ce nouveau forfait. Chaque employé de l'opérateur effectue 60 appels par jour. On suppose le fichier suffisamment important pour que les choix soient considérés réalisés de façon indépendante et dans des conditions identiques. On note X la variable aléatoire qui comptabilise le nombre de souscriptions réalisées par un employé donné un jour donné.

1. Justifier que la variable aléatoire $X$ suit une loi binomiale dont on donnera les paramètres.
2. Déterminer la probabilité que l'employé obtienne 5 souscriptions un jour donné. On arrondira le résultat au centième.
3. Déterminer la probabilité que l'employé obtienne au moins une souscription un jour donné. On donnera une valeur arrondie au dix-millième.

Corrigé

Partie A

1. Arbre de probabilité complété.

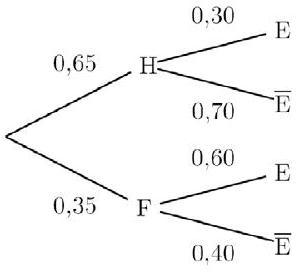
2．a．$E \cap F:$ « la personne choisie est une femme qui écoute les explications du démarcheur »． $p(E \cap F)=p(F \cap E)=p(F) \times p_{F}(E)=0,35 \times 0,60=0,21$.

2．b．La probabilité cherchée est $p(E)=p(H \cap E)+p(F \cap E)$（par application de la formule des probabilités totales）． Soit ：$p(E)=p(H) \times p_{H}(E)+0,21$ ． Soit ：$p(E)=0,65 \times 0,30+0,21=0,195+0,21=0,405$ ．

2．c．La probabilité cherchée est $p_{E}(H)=\frac{p(H \cap E)}{p(E)}=\frac{0,195}{0,405} \approx 0,48$ ．

Partie B

1．L＇expérience consiste à répéter 60 fois de manière indépendante une expérience à 2 issues ： S：«la personne souscrit au forfait»． E：«la personne ne souscrit pas au forfait»． On a $p(S)=0,12$ ． X dénombre les succès． On en déduit que $X$ suit une loi binomiale de paramètres $n=60$ et $p=0,12$ ．

2．À la calculatrice，on obtient：$p(X=5) \approx 0,120$ ．

3．On cherche $p(X \geq 1)$ ． Or $p(X \geq 1)=1-p(X<1)=1-p(X=0)$ ． Et à la calculatrice，on obtient ：$p(X=0) \approx 0,0005$ ． Donc $p(X \geq 1) \approx 0,9995$ ．

Exercice 5

Le plan est rapporté à un repère orthonormé d＇origine O ． Un robot est situé en O et il va rejoindre le point $\mathrm{M}(7 ; 9)$ en $n$ étapes． À chaque étape，soit il effectue une translation de vecteur $\vec{\imath}(1 ; 0)$ ，soit il effectue une translation de vecteur $\vec{J}(0 ; 1)$ ． On notera，si besoin ： $\mathbf{i}$ ：«le robot effectue une translation de vecteur $\vec{\imath}$ » j：«le robot effectue une translation de vecteur $\vec{J}$ » 1．Combien vaut $n$ ？ 2．Combien de chemins différents permettent au robot d＇atteindre le point M ？ 3．Le robot effectue 16 étapes．

À chaque fois, les événements $i$ et $j$ sont équiprobables. Quelle est la probabilité que le robot arrive en M (arrondie à 0,01 )? 4. Cette fois-ci, le robot effectue toujours 16 étapes, mais, à chaque fois, ses choix ne sont pas équiprobables. On a : $p(i)=0,4$, et par là, $p(j)=0,6$. Quelle est la probabilité que le robot arrive en $M$ ? (arrondie à 0,01 )

Corrigé

1. Le robot va rejoindre le point $\mathrm{M}(7 ; 9)$ en $n$ étapes.

Pour atteindre le point M , le robot doit effectuer : 7 translations de vecteur $\vec{\imath}(1 ; 0)$ et 9 translations de vecteur $\vec{\jmath}(0 ; 1)$. Or $7+9=16$. Donc $n=16$. 2. Un chemin possible correspond à une combinaison de 7 éléments pris parmi 16, qui sont les rangs des 7 translations. Par exemple, ${1,2,4,5,9,12,13}$ code le chemin suivant : (i, i, j, i, i, j, j, j, i, j, j, i, i, j, j, j). Or $\binom{16}{7}=11440$. Donc il y a 11440 chemins possibles ! 3. Le nombre de chemins possibles est $2^{16}=65635$. Ils sont équiprobables. Or 11440 de ces chemins conduisent à M. Donc la probabilité cherchée vaut $\frac{11440}{65635} \approx 0,17$.

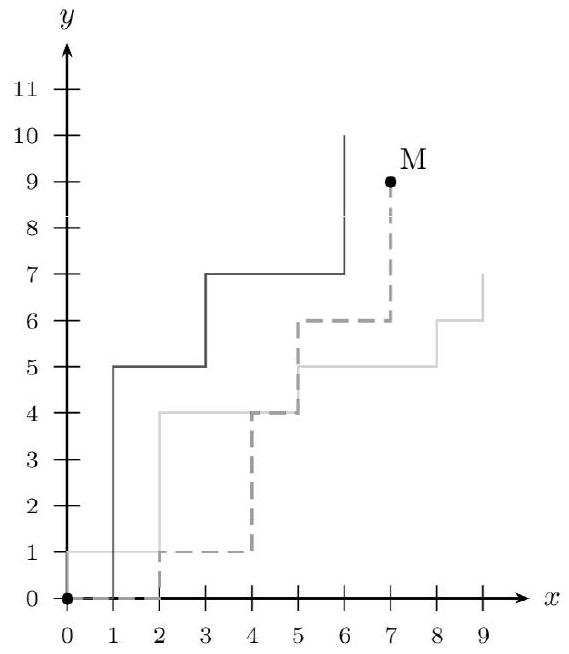
Sur le schéma ci-dessus, seul le chemin en traits interrompus est favorable. 4. Cette fois-ci, les chemins ne sont pas équiprobables. Nous devons raisonner autrement.

Chacune des étapes constitue une épreuve de Bernoulli de paramètre $p=0,4$ et dont le succès est i.

Les 16 étapes sont indépendantes. Soit X la variable aléatoire dénombrant les succès. Par conséquent $X$ est une binomiale de paramètres 16 et 0,4 . Soit : $X=B(16 ; 0,4)$. La probabilité cherchée est : $p(X=7)=\binom{16}{7} 0,4^{7}(1-0,4)^{16-7}=11440 \times 0,4^{7} \times 0,6^{9} \approx 0,19$. À la calculatrice, on peut obtenir directement : $p(X=7) \approx 0,19$.

Exercice 6

Le directeur d'un hôtel tente de louer toutes ses chambres malgré les défections de quelques clients. Il a instauré un système de réservations et a constaté que 20 % des clients réservent par téléphone, les autres utilisent internet. Mais certains clients ayant réservé ne viennent pas; cela concerne $4 %$ des clients ayant réservé par téléphone, et $10 %$ des clients ayant réservé par internet. On considère une réservation prise au hasard. Soit T: «la réservation a été faite par téléphone»; I: «la réservation a été faite par Internet»; P : «le client se présente à l'hôtel».

1. Représenter la situation par un arbre de probabilité.

Montrer que $p(P)=0,912$ 2. On considère un client présent dans l'hôtel.

Quelle est la probabilité qu'il ait réservé par internet (arrondie au millième) ? 3. Le directeur sait qu'il ne peut accueillir que 100 clients. Mais il a accordé 106 réservations. Soit X la variable aléatoire qui dénombre les clients qui se présentent à l'hôtel. Justifier que la variable aléatoire $X$ suit une loi binomiale dont on donnera les paramètres. 4. Quelle est la probabilité (arrondie à $10^{-5}$ ) que les 106 clients se présentent à l'hôtel? 5. Quelle est la probabilité, arrondie au centième, que le directeur se retrouve en situation de surréservation (c'est-à-dire qu'au moins 101 clients se présentent à l'hôtel) ? 6. Quel est le nombre maximum de réservations que doit accorder le directeur pour être certain à $99 %$ que tous les clients qui se présenteront à l'hôtel aient une chambre?

Corrigé

1. Voici un arbre de probabilité convenable. ${T ; I}$ constitue une partition de l'univers. On sait que $p(P)=p(T \cap P)+p(I \cap P)$ (par application de la formule des probabilités totales). Soit: $p(P)=p(T) \times p_{T}(P)+p(I) \times p_{I}(P)$. Soit : $p(P)=0,20 \times 0,96+0,80 \times 0,90$. Et donc : $p(P)=0,912$.
2. On cherche : $p_{P}(I)=\frac{p(I \cap P)}{p(P)}=\frac{0,80 \times 0,90}{0,912} \approx 0,789$.
3. Le directeur sait qu'il ne peut accueillir que 100 clients. Mais il a accordé 106 réservations. Soit X la variable aléatoire qui dénombre les clients qui se présentent à l'hôtel. L'expérience consiste à répéter 106 fois de manière indépendante une expérience à 2 issues: $P$ et $\bar{P}$, et on a $p(P)=0,912$. On en déduit que X suit une loi binomiale de paramètres $n=106$ et $p=0,912$.
4. On cherche : $p(X=106)=0,912^{106} \approx 6 \times 10^{-5}$.
5. On cherche : $p(X \geq 101)=p(101 \leq X \leq 106)$.

Soit : $p(X \geq 101)=p(X \leq 106)-p(X \leq 100) \approx 1-0,91 \approx 0,09$. 6. On cherche le plus grand entier $n$ tel que $p(Y \leq 100) \geq 0,99$, où Y est la binomiale de paramètres $n$ inconnu et $p=0,912$. Par essais successifs, on obtient: pour $n=104, p(Y \leq 100) \approx 0,984$, pour $n=103, p(Y \leq 100) \approx 0,995$. Donc le directeur doit accorder au plus 103 réservations pour être certain à $99 %$ que tous les clients qui se présenteront à l'hôtel auront une chambre.