Exercices : Intégrales

Exercices corrigés

Exercice 1

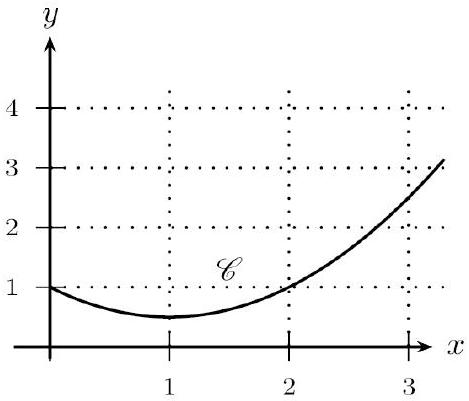
Soit $f$ de courbe représentative $C$ dans un repère orthogonal. Soit : $A=\int_{1}^{3} f(t) d t$. Déterminer graphiquement quel encadrement est correct :

• $1 \leq A \leq 2$
• $2 \leq A \leq 3$
• $3 \leq A \leq 4$

Corrigé

$f$ est clairement continue et positive sur $[1 ; 3]$. Et de ce fait $A$ est l'aire du domaine $D={M(x ; y) / 1 \leq x \leq 3$ et $0 \leq y \leq f(x)}$. Il suffit donc de déterminer graphiquement l'aire de la partie hachurée sous la courbe donnée.

Rappelons que cette aire est exprimée en unités d'aires. D'ailleurs, une unité d'aire est visualisée par le rectangle situé au-dessusde la courbe. Il suffit donc de compter combien de rectangles donnent la même aire que celle de $D$. La réponse correcte est donc : $2 \leq A \leq 3$

Exercice 2

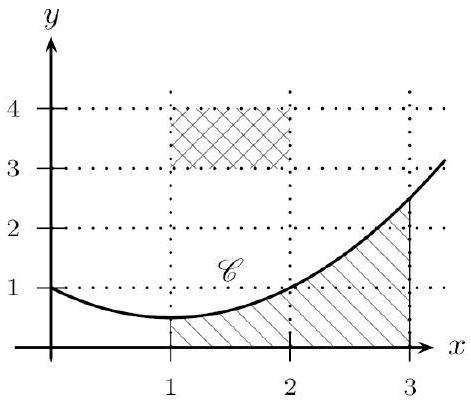
Le plan est raporté à un repère orthogonal (unités : $1,2 \mathrm{~cm}$ sur l'axe des abscisses et $0,8 \mathrm{~cm}$ sur l'axe des ordonnées).

Soit $f$ de courbe représentative $C$ dans ce repère orthogonal. $f$ est définie sur [ $0 ; 4$ ] par : $f(x)=1$ pour $x$ dans [0;2], $f(x)=0,5 x$ pour $x$ dans $] 2 ; 4]$.

On admettra que $f$ est continue et positive sur $[0 ; 4]$. Déterminer la valeur de : $A=\int_{0}^{4} f(t) d t$. Quelle est l'aire de la partie hachurée (en $\mathrm{cm}^{2}$ ) ?

Corrigé

$f$ est continue et positive sur $[0 ; 4]$. Et de ce fait $A$ est l'aire du domaine $D={M(x ; y) / 0 \leq x \leq 4$ et $0 \leq y \leq f(x)}$. Cela correspond au domaine hachuré du graphique. En appliquant la relation de Chasles, on obtient :

$$ A=\int_{0}^{4} f(t) d t=\int_{0}^{2} f(t) d t+\int_{2}^{4} f(t) d t $$

Or $\int_{0}^{2} f(t) d t$ est l'aire du rectangle (hachuré à gauche) de côtés 2 et 1 . Donc : $\int_{0}^{2} f(t) d t=2 \times 1=2$. Et $\int_{2}^{4} f(t) d t$ est l'aire du trapèze (hachuré à droite) de bases $f(2)=1$ et $f(4)=2$ et de hauteur $4-2=2$. Donc : $\int_{2}^{4} f(t) d t=\frac{1+2}{2} \times 2=3$. Et finalement : $A=2+3=5$.

Soit : $A=5$. Cela correspond à l'aire du domaine hachuré (en unités d'aires). Or 1 unité d'aire est la surface d'un rectangle de côtés 1,2 et 0,8 . Et comme $1,2 \times 0,8=0,96$, une unité d'aire mesure $0,96 \mathrm{~cm}^{2}$. On calcule alors : $5 \times 0,96=4,8$. Finalement, l'aire de la partie hachurée est de $4,8 \mathrm{~cm}^{2}$.

Exercice 3

Donner la valeur exacte de :

1. $A=\int_{1}^{3} f(t) d t$ où $f$ est définie par $f(x)=e^{x}-x^{2}+2 x-8$ sur $\mathbb{R}$.
2. $B=\int_{-2}^{3} d t$
3. $C=\int_{0}^{1}\left(3 t^{2} e^{t^{3}+4}\right) d t$
4. $D=\int_{1}^{2}\left(\frac{6}{t}+3 t+4\right) d t$
5. $E=\int_{0,5}^{1} \frac{3}{t^{2}} d t$
6. $F=\int_{0}^{1}\left(e^{x}+e^{-x}\right) d x$

Corrigé

1. $f$ admet pour primitive $F(x)=e^{x}-\frac{x^{3}}{3}+x^{2}-8 x$.

On obtient : $A=\int_{1}^{3} f(t) d t=[F(x)]_{1}^{3}=F(3)-F(1)$.

Soit :

$$ A=\int_{1}^{3} f(t) d t=\left(e^{3}-\frac{3^{3}}{3}+3^{2}-8 \times 3\right)-\left(e^{1}-\frac{1^{3}}{3}+1^{2}-8 \times 1\right) $$

Soit : $A=\left(e^{3}-9+9-24\right)-\left(e-\frac{1}{3}+1-8\right)$ Soit : $A=e^{3}-24-e+\frac{1}{3}+7=e^{3}-e-\frac{50}{3}$. 2. $B=\int_{-2}^{3} d t=\int_{-2}^{3} 1 d t=[t]_{-2}^{3}=3-(-2)=5$. 3. On sait que $u^{\prime} e^{u}$ a pour primitive $e^{u}$. Ici : $u=t^{3}+4$ et $u^{\prime}=3 t^{2}+0=3 t^{2}$.

D'où : $C=\int_{0}^{1}\left(3 t^{2} e^{t^{3}+4}\right) d t=\left[e^{t^{3}+4}\right]{0}^{1}=e^{1^{3}+4}-e^{0^{3}+4}=e^{5}-e^{4}$. 4. $\quad D=\int{1}^{2}\left(\frac{6}{t}+3 t+4\right) d t=\int_{1}^{2}\left(6 \frac{1}{t}+3 t+4\right) d t=\left[6 \ln t+3 \frac{t^{2}}{2}+4 t\right]_{1}^{2}$.

Soit: $D=\left(6 \ln 2+3 \frac{2^{2}}{2}+4 \times 2\right)-\left(6 \ln 1+3 \frac{1^{2}}{2}+4 \times 1\right)$. Soit: $D=6 \ln 2+6+8-(6 \times 0+1,5+4)$. Soit : $D=6 \ln 2+14-5,5=6 \ln 2+8,5$. 5. $\quad E=\int_{0,5}^{1} \frac{3}{t^{2}} d t=\int_{0,5}^{1} 3 \frac{1}{t^{2}} d t=\left[3 \frac{-1}{t}\right]{0,5}^{1}=\left[\frac{-3}{t}\right]{0,5}^{1}$.

Soit : $E==\frac{-3}{1}-\frac{-3}{0,5}=-3+6=3$. 6. On sait que $e^{x}$ admet pour primitive $e^{x}$, et que $e^{-x}$ admet pour primitive $-e^{-x}$.

Donc : $\quad F=\int_{0}^{1}\left(e^{x}+e^{-x}\right) d x=\left[e^{x}-e^{-x}\right]_{0}^{1}=e^{1}-e^{-1}-\left(e^{0}-e^{-0}\right)$. Soit : $F=e-\frac{1}{e}-(1-1)=e-\frac{1}{e}$.

Exercice 4

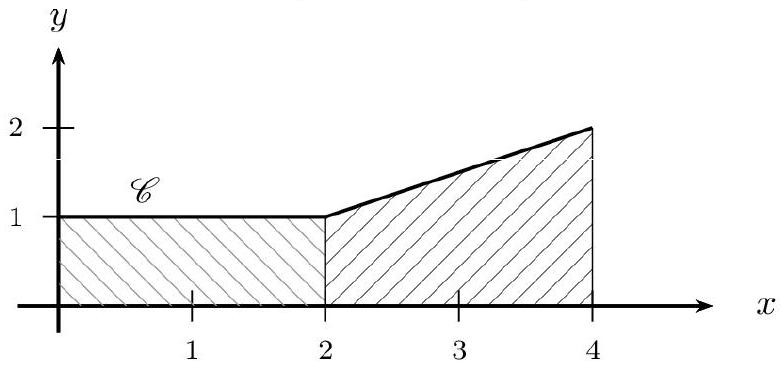
Soit $f$ définie par $f(x)=0,5 x^{2}-x+1$ de courbe représentative $C$ dans un repère orthogonal (unités : $1,2 \mathrm{~cm}$ sur l'axe des abscisses, $0,6 \mathrm{~cm}$ sur l'axe des ordonnées).

1. Montrer que $f$ est continue et positive sur $[1 ; 3]$.
2. On considère le domaine $D={M(x ; y) / 1 \leq x \leq 3$ et $0 \leq y \leq f(x)}$.

Représenter graphiquement $C$ pour $x$ dans $[0 ; 3,3]$ et hachurer $D$. 3. Déterminer l'aire $A$ du domaine $D$ (en $\mathrm{cm}^{2}$ ).

Corrigé

1. La fonction $f$ est un trinôme; c'est une fonction usuelle. Elle est donc continue.

Avec les conventions habituelles : $a=0,5, \quad b=-1 \quad$ et $\quad c=1$. $\Delta=b^{2}-4 a c=(-1)^{2}-4 \times 0,5 \times 1=1-2=-1$. $\Delta<0$, et par là, $f(x)$ est du signe de $a$, c'est-à-dire strictement positif, pour tout $x$ 2. $f$ étant un trinôme, $C$ est donc une parabole. Son sommet a pour abscisse $\frac{-b}{2 a}=12 \times 0,5=1$. Comme $a>0, f$ est d'abord décroissante, puis croissante. Quelques valeurs permettent de tracer la courbe ci-après. Le domaine $D$ est la partie hachurée sous la courbe.

$x$	0	1	2	3,3
$f(x)$	1	0,5	2,5	3,145

3. La fonction $f$ étant continue et positive sur $[1 ; 3]$, on a : $A=\int_{1}^{3} f(t) d t$.

Soit : $\quad A=\int_{1}^{3}\left(0,5 x^{2}-x+1\right) d x=\left[0,5 \frac{x^{3}}{3}-\frac{x^{2}}{2}+x\right]_{1}^{3}$. Soit : $A=\left(0,5 \frac{3^{3}}{3}-\frac{3^{2}}{2}+3\right)-\left(0,5 \frac{1^{3}}{3}-\frac{1^{2}}{2}+1\right)$. Soit : $A=(0,5 \times 9-4,5+3)-\left(0,5 \frac{1}{3}-0,5+1\right)$. Soit : $A=4,5-4,5+3-\frac{0,5}{3}+0,5-1$. Soit : $A=2,5-\frac{0,5}{3}=\frac{5}{2}-\frac{1}{6}=\frac{15}{6}-\frac{1}{6}=\frac{14}{6}=\frac{7}{3}$. Donc l'aire $A$ est égale à $\frac{7}{3}$ unités d'aire. Or : $1,2 \times 0,6=0,72$. Donc une unité d'aire mesure $0,72 \mathrm{~cm}^{2}$ (c'est la surface du rectangle hachuré). Et comme $\frac{7}{3} \times 0,72=1,68$, l'aire $A$ vaut $1,68 \mathrm{~cm}^{2}$.

Exercice 5

Soit $f$ définie par $f(x)=0,5 e^{2 x-3}+1$. $f$ est représentée dans un repère orthogonal par la courbe $C$ ci-dessous.

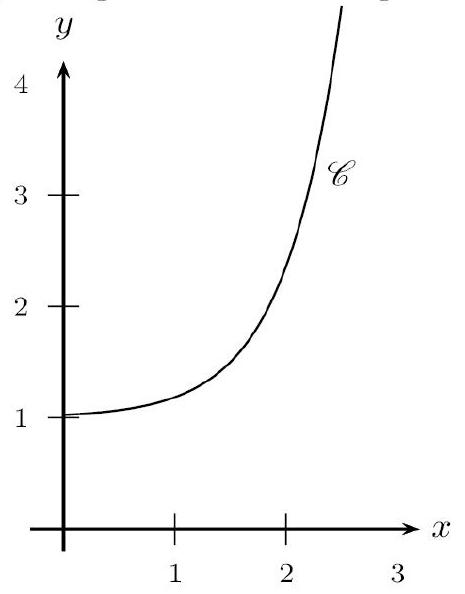
1. Pourquoi $f$ est-elle positive et continue sur $\mathbb{R}$ ?
2. Déterminer la valeur moyenne $m$ de $f$ sur $[0 ; 2]$.
3. Interpréter graphiquement.

Corrigé

1. La fonction $f$ est obtenue par opérations et par composition usant de fonctions usuelles, par là, elle est donc continue. On sait que $e^{2 x-3}>0$. De plus $0,5>0$. Donc $0,5 e^{2 x-3}>0$. Par conséquent : $0,5 e^{2 x-3}+1>1$. Et $f$ est donc strictement positive.
2. On obtient: $m=\frac{1}{2-0} \int_{0}^{2} f(t) d t=\frac{1}{2} \int_{0}^{2}\left(0,5 e^{2 x-3}+1\right) d x=\frac{1}{2} \int_{0}^{2}\left(\frac{1}{4} 2 e^{2 x-3}+1\right) d x$ Soit : $m=\frac{1}{2}\left[\frac{1}{4} e^{2 x-3}+x\right]_{0}^{2}=\frac{1}{2}\left(\left(\frac{1}{4} e^{2 \times 2-3}+2\right)-\left(\frac{1}{4} e^{2 \times 0-3}+0\right)\right.$. Soit : $m=\frac{1}{2}\left(\frac{1}{4} e+2-\frac{1}{4} e^{-3}\right) \approx 1,33$.
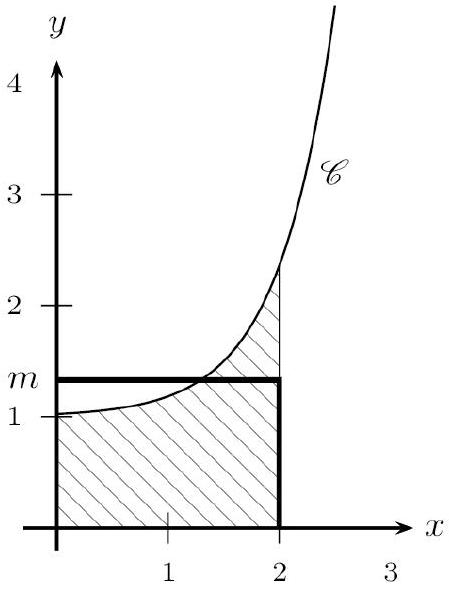
3. La fonction $f$ étant continue et positive sur $[1 ; 3], \int_{1}^{3} f(t) d t$ est l'aire située entre $C$, l'axe des abscisses, les droites d'équation $x=0$ et $x=2$. Cette aire est la même que celle du rectangle de côtés $m$ et $2-0=2$.

Exercice 6

Soit $f$ la fonction définie sur l'intervalle $] 0 ;+\infty\left[\operatorname{par} f(x)=\frac{1+\ln x}{x^{2}}\right.$ et soit $C$ la courbe représentative de la fonction $f$ dans un repère du plan. La courbe $C$ est donnée ci-après : 1.a. Déterminer la limite de $f$ en 0 . 1.b. Que vaut $\lim _{x \rightarrow+\infty} \frac{\ln x}{x}$. En déduire la limite de $f$ en $+\infty$. 1.c. En déduire les asymptotes éventuelles à la courbe $C$. 2.a. On note $f^{\prime}$ la fonction dérivée de $f$ sur l'intervalle $] 0 ;+\infty[$.

Démontrer que, pour tout $x$ de $] 0 ;+\infty\left[\right.$, on a : $f^{\prime}(x)=\frac{-1-2 \ln x}{x^{3}}$. 2.b. Résoudre sur l'intervalle $] 0 ;+\infty[$ l'inéquation : $-1-2 \ln x>0$. 2.c. Dresser le tableau de variations de $f$ sur l'intervalle $] 0 ;+\infty[$. 3.a. Démontrer que $C$ admet un unique point d'intersection avec l'axe des abscisses. Préciser les coordonnées de ce point. 3.b. En déduire le signe de $f(x)$ sur l'intervalle $] 0 ;+\infty[$. 4.a. Démontrer que la fonction $F$, définie sur l'intervalle $] 0 ;+\infty\left[\operatorname{par} F(x)=\frac{-2-\ln x}{x}\right.$ est une primitive de la fonction $f$ sur l'intervalle $] 0 ;+\infty[$. 4.b. Pour tout entier $n \geq 1$, on note $I_{n}$ l'aire (en unités d'aire) du domaine $D_{n}$ délimité par $C$, l'axe des abscisses, et les droites d'équations $x=\frac{1}{e}$ et $x=n$. Calculer $I_{n}$ en fonction de $n$. 4.c. Étudier la limite de la suite $\left(I_{n}\right)_{n \in \mathbb{N}}$.

Interpréter graphiquement le résultat obtenu.

Corrigé

1.a. On note que : $f(x)=(1+\ln x) \frac{1}{x^{2}}$.

On a : $\lim _{x \rightarrow 0} 1=1$ et $\lim _{x \rightarrow 0} \ln x=-\infty$. Donc : $\lim _{x \rightarrow 0} 1+\ln x=-\infty$. Par ailleurs : $\lim _{x \rightarrow 0} \frac{1}{x^{2}}=+\infty$. Par conséquent, on obtient : $\lim _{x \rightarrow 0}(1+\ln x) \frac{1}{x^{2}}=-\infty$ (limite d'un produit). Soit : $\lim _{x \rightarrow 0} f(x)=-\infty$. 1.b. On sait que : $\lim _{x \rightarrow+\infty} \frac{\ln x}{x}=0$.

On fait apparaître ce terme dans l'expression de $f(x)$. On obtient : $f(x)=\left(\frac{1}{x}+\frac{\ln x}{x}\right) \frac{1}{x}$. Or : $\lim _{x \rightarrow+\infty} \frac{1}{x}=0$. Par conséquent : $\lim _{x \rightarrow+\infty}\left(\frac{1}{x}+\frac{\ln x}{x}\right) \frac{1}{x}=(0+0) \times 0=0$. Soit : $\lim _{x \rightarrow+\infty} f(x)=0$ 1.c. D'après le 1.a., l'axe des ordonnées est asymptote à la courbe $C$.

D'après le 1.b., l'axe des abscisses est asymptote à la courbe $C$ en $+\infty$. 2.a. On pose: $u=1+\ln x$ et $v=x^{2}$.

Oa a alors : $u^{\prime}=0+\frac{1}{x}=\frac{1}{x}$ et $v^{\prime}=2 x$. Ici : $f=\frac{u}{v}$ et $f^{\prime}=\frac{u^{\prime} v-u v^{\prime}}{v^{2}}$. Donc : $f^{\prime}(x)=\frac{\frac{1}{x} x^{2}-(1+\ln x) 2 x}{x^{4}}=\frac{x-2 x-2 x \ln x}{x^{4}}=\frac{-x-2 x \ln x}{x^{4}}=\frac{x(-1-2 \ln x)}{x^{4}}$. Soit : $f^{\prime}(x)=\frac{-1-2 \ln x}{x^{3}}$. 2.b. On résout sur $] 0 ;+\infty[$.

On a : $-1-2 \ln x>0 \Leftrightarrow-1>2 \ln x \Leftrightarrow-0,5>\ln x \Leftrightarrow e^{-0,5}>e^{\ln x} \Leftrightarrow$ $e^{-0,5}>x$. Par conséquent : $S=] 0 ; e^{-0,5}[$. 2.c. $f$ admet le tableau de variations situé page suivante.

Notons que : $f\left(e^{-0,5}\right)=\frac{1+\ln e^{-0,5}}{\left(e^{-0,5}\right)^{2}}=\frac{1-0,5 \ln e}{e^{-1}}=\frac{1-0,5}{e^{-1}}=\frac{0,5}{e^{-1}}=0,5 e$.

$x$	0		$e^{-0,5}$		$+\infty$
$-1-2 \ln x$		+	0	-
$x^{3}$	0	+	1	+
$f^{\prime}(x)$		+	0	-
			$0,5 e$
$f(x)$
					0

3.a. On résout sur $] 0 ;+\infty\left[: f(x)=0 \Leftrightarrow \frac{1+\ln x}{x^{2}}=0 \Leftrightarrow 1+\ln x=0 \Leftrightarrow \ln x=-1 \Leftrightarrow\right.$ $x=e^{-1}=\frac{1}{e}$. L'équation admet une solution et une seule. Donc $C$ admet un unique point d'intersection avec l'axe des abscisses. Ce point a pour abscisse $\frac{1}{e}$. Son ordonnée vaut évidemment 0 . Pour les anxieux... Vérification : $f\left(\frac{1}{e}\right)=\frac{1+\ln \frac{1}{e}}{\left(\frac{1}{e}\right)^{2}}=(1-1) e^{2}=0$. 3.b. Finalement, d'après le 3.a. et le tableau de variation, on en déduit alors que $f$ est strictement négative sur $] 0 ; \frac{1}{e}[$, et strictement positive sur $] \frac{1}{e} ;+\infty[$. 4.a. Montrons que $F^{\prime}=f$ sur l'intervalle $] 0 ;+\infty[$.

On pose: $u=-2-\ln x$ et $v=x$. Oa a alors : $u^{\prime}=0-\frac{1}{x}=\frac{-1}{x}$ et $v^{\prime}=1$. Ici : $F=\frac{u}{v}$ et $F^{\prime}=\frac{u^{\prime} v-u v^{\prime}}{v^{2}}$. Donc : $F^{\prime}(x)=\frac{\frac{-1}{x} x-(-2-\ln x) \times 1}{x^{2}}=\frac{-1+2+\ln x}{x^{2}}=\frac{1+\ln x}{x^{2}}=f(x)$. Donc la fonction $F$, définie sur l'intervalle $] 0 ;+\infty\left[\operatorname{par} F(x)=\frac{-2-\ln x}{x}\right.$ est bien une primitive de la fonction $f$ sur l'intervalle $] 0 ;+\infty[$. 4.b. Soit $n$ un entier tel que $n \geq 1$.

La fonction $f$ étant continue (car dérivable) et positive sur $\left[\frac{1}{e} ; n\right]$ (d'après le 3.b.), on en déduit que : $I_{n}=\int_{\frac{1}{e}}^{n} f(x) d x$. Donc : $I_{n}=F(n)-F\left(\frac{1}{e}\right)=\frac{-2-\ln n}{n}-\frac{-2-\ln \left(\frac{1}{e}\right)}{\frac{1}{e}}$. Soit : $I_{n}=\frac{-2-\ln n}{n}-(-2-(-1)) e=\frac{-2-\ln n}{n}+e$. Soit : $I_{n}=\frac{-2-\ln (n)}{n}+e$. 4.c. On obtient facilement $\lim _{n \rightarrow+\infty}-2-\ln n=-\infty$ et $\lim _{n \rightarrow+\infty} n=+\infty$, ce qui conduit à une forme indéterminée. On factorise alors le terme dominant du numérateur. $\frac{-2-\ln n}{n}=\frac{\ln n\left(\frac{-2}{\ln n}-1\right)}{n}=\frac{\ln n}{n}\left(\frac{-2}{\ln n}-1\right)$. Or: $\lim _{n \rightarrow+\infty} \ln n=+\infty$, et par là : $\lim _{n \rightarrow+\infty} \frac{-2}{\ln n}-1=0-1=-1$. Or : $\lim _{n \rightarrow+\infty} \frac{\ln n}{n}=0$. Donc : $\lim _{n \rightarrow+\infty} \frac{\ln n}{n}\left(\frac{-2}{\ln n}-1\right)=0 \times(-1)=0$. Et finalement : $\lim {n \rightarrow+\infty} I{n}=0+e=e$. Autre méthode (qui fonctionne dans ce cas particulier) : On a : $\frac{-2-\ln n}{n}=\frac{-2}{n}-\frac{\ln n}{n}$.

Comme : $\lim {n \rightarrow+\infty} \frac{\ln n}{n}=0$ et : $\lim {n \rightarrow+\infty} \frac{-2}{n}=0$, on obtient : $\lim {n \rightarrow+\infty} I{n}=0+0+e=e$. Quelle que soit la méthode, on a finalement : $\lim {n \rightarrow+\infty} I{n}=e$. On en déduit que l'aire du domaine $D{n}$ tend vers $e$ lorsque $n$ tend vers $+\infty$. Le domaine $D{n}$ est hachuré ci-dessous.

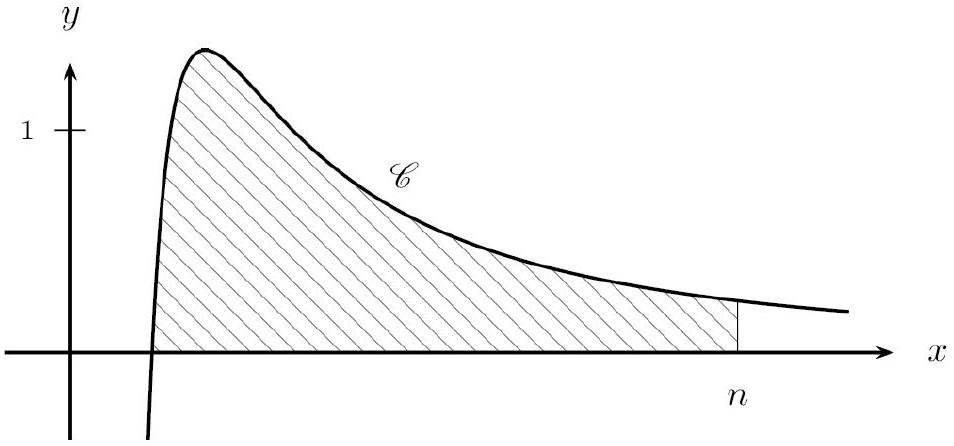
On notera que, comme $\lim {n \rightarrow+\infty} I{n}=e$, l'aire du domaine infini délimité par $C$, l'axe des abscisses, et la droite d'équation $x=\frac{1}{e}$ vaut e. Nous sommes en présence d'un domaine de taille infinie qui possède une aire finie.

Exercice 7

Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=x e^{-x}$ et soit $C$ la courbe représentative de la fonction $f$ dans un repère du plan. 1.a. Déterminer la limite de $f$ en $-\infty$. 1.b. Déterminer la limite de $f$ en $+\infty$. 1.c. En déduire les asymptotes éventuelles à la courbe $C$. 2.a. On note $f^{\prime}$ la fonction dérivée de $f$ sur $\mathbb{R}$.

Démontrer que, pour tout $x$ de $\mathbb{R}$, on a : $f^{\prime}(x)=e^{-x}(1-x)$. 2.b. Dresser le tableau de variations de $f$ sur $\mathbb{R}$. 3. Soit $g$ la fonction définie sur $\mathbb{R}$ par $g(x)=-(x+1) e^{-x}$.

Montrer que $g$ est une primitive de $f$ sur $\mathbb{R}$. 4. Étudier le signe de $f(x)$ sur $\mathbb{R}$. 5. On note $A$ l'aire (en unités d'aire) du domaine $D$ délimité par $C$, l'axe des abscisses, et les droites d'équations $x=0$ et $x=\ln 10$. Déterminer la valeur exacte, puis une valeur arrondie au centième de $A$.

Corrigé

1.a. On a: $\lim _{x \rightarrow-\infty}-x=+\infty$.

Or: $\lim _{y \rightarrow+\infty} e^{y}=+\infty$. Donc : $\lim _{x \rightarrow-\infty} e^{-x}=+\infty$ (limite d'une composée). Par ailleurs : $\lim _{x \rightarrow-\infty} x=-\infty$. Donc, finalement : $\lim _{x \rightarrow-\infty} x e^{-x}=-\infty$ (limite d'un produit). Soit : $\lim _{x \rightarrow-\infty} f(x)=-\infty$. 1.b. On sait que : $\lim _{x \rightarrow+\infty} \frac{e^{x}}{x}=+\infty$, et donc que : $\lim _{x \rightarrow+\infty} \frac{x}{e^{x}}=0$.

Soit : $\lim _{x \rightarrow+\infty} x e^{-x}=0$. Soit : $\lim _{x \rightarrow+\infty} f(x)=0$. 1.c. D'après le 1.b., l'axe des abscisses est asymptote à la courbe $C$ en $+\infty$. 2.a. On pose : $u=x$ et $v=e^{-x}$.

Oa a alors : $u^{\prime}=1$ et $v^{\prime}=(-1) e^{-x}=-e^{-x}$. Ici : $f=u v$ et $f^{\prime}=u^{\prime} v+u v^{\prime}$. Donc : $f^{\prime}(x)=1 e^{-x}+x\left(-e^{-x}\right)=e^{-x}(1-x)$. Soit : $f^{\prime}(x)=e^{-x}(1-x)$. 2.b. On note que $e^{-x}$ reste strictement positif pour tout réel $x$.

Par conséquent, $f^{\prime}(x)$ est du signe de $1-x$ (fonction affine de c.d. négatif s'annulant en 1). D'où le tableau de signes de $f^{\prime}$ et de variations de $f$ ci-dessous :

$x$	$-\infty$		1		$+\infty$
$f^{\prime}(x)$		+	$\emptyset$	-
			$e^{-1}$
$f(x)$
	$-\infty$				0

Notons que : $f(1)=e^{-1}$. 3. On pose : $u=-(x+1)=-x-1$ et $v=e^{-x}$.

Oa a alors : $u^{\prime}=-1$ et $v^{\prime}=(-1) e^{-x}=-e^{-x}$. Ici : $g=u v$ et $g^{\prime}=u^{\prime} v+u v^{\prime}$. Donc : $g^{\prime}(x)=-1 e^{-x}+(-x-1)\left(-e^{-x}\right)=e^{-x}(-1+x+1)=x e^{-x}=f(x)$. Donc $g^{\prime}=f$ sur $\mathbb{R}$. Et par là, $g$ est bien une primitive de $f$ sur $\mathbb{R}$. 4. On note que $e^{-x}$ reste strictement positif pour tout réel $x$.

Par conséquent, $f(x)$ est du signe de $x$. Pour $x<0$, on a: $f(x)<0$. Pour $x=0$, on a: $f(x)=0$. Pour $x>0$, on a: $f(x)>0$. 5. La fonction $f$ est continue (car dérivable) et positive sur $\mathbb{R}$ (d'après le 4.).

Elle l'est donc en particulier sur $[0 ; \ln 10]$. Par conséquent : $A=\int_{0}^{\ln 10} f(x) d x$. Soit : $A=[g(x)]_{0}^{\ln 10}=g(\ln 10)-g(0)=-(\ln 10+1) e^{-\ln 10}-\left(-(0+1) e^{-0}\right)$. Soit : $A=-(\ln 10+1)\left(e^{\ln 10}\right)^{-1}+1=-(\ln 10+1)(10)^{-1}+1=1-\frac{\ln 10+1}{10}$. Soit : $A=\frac{9-\ln 10}{10}$.

Et donc : $A \approx 0,67$ (unités d'aire).

Exercice 8

Soit $f$ la fonction définie par $f(x)=\frac{1}{x}-1$. et soit $C$ la courbe représentative de la fonction $f$ dans un repère orthonormal du plan. Une portion de la courbe $C$ est représentée ci-après. L'aire du domaine hachuré en haut est égale à l'aire du domaine hachuré en bas. Que vaut $a$ ? Vous en déterminerez la valeur exacte, puis une valeur approchée arrondie au millième.

Dans cet exercice, toute trace de recherche, même non aboutie, serait prise en compte pour la notation.

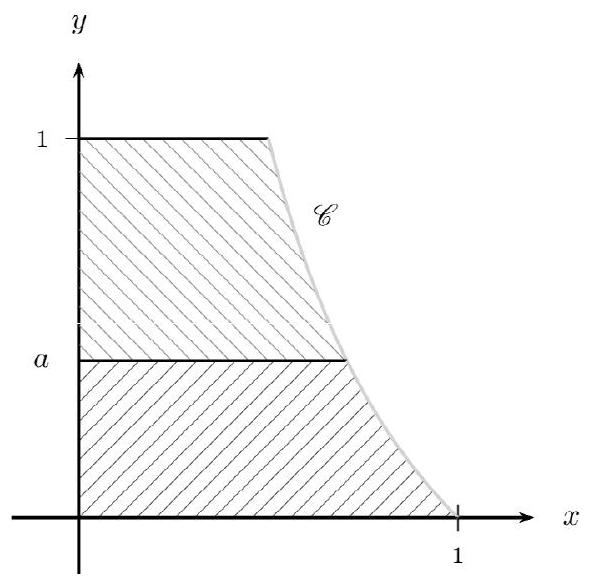
Corrigé

Soit $x_{1}$ et $x_{a}$ les antécédents respectifs de 1 et de $a$ par la fonction $f$. Ces réels sont marqués sur le dessin qui suit. Appelons $A_{t}$ l'aire du domaine constitué de la réunion du domaine hachuré en haut et du domaine hachuré en bas. Appelons $A_{n}$ l'aire du domaine hachuré en bas. Nous avons donc l'égalité : $A_{t}=2 A_{n}$. Cette égalité va nous fournir une équation dont $a$ est solution.

Mais calculons tout d'abord chacune des 2 aires.

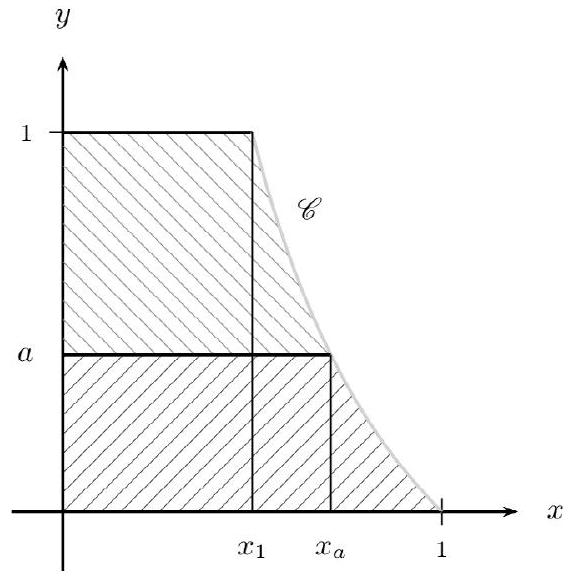
Les aires considérées étant celles de domaines situés entre des courbes de fonctions continues positives et l'axe des abscisses, on obtient :

$$ A_{t}=\int_{0}^{x_{1}} 1 d x+\int_{x_{1}}^{1} f(x) d x $$

Or，une primitive de 1 est $x$ ，et une primitive de $f(x)$ est $\ln x-x$ ． Donc ：$A_{t}=[x]{0}^{x{1}}+[\ln x-x]{x{1}}^{1}$ ． Soit ：$A_{t}=x_{1}-0+(\ln 1-1)-\left(\ln x_{1}-x_{1}\right)$ ． Soit ：$A_{t}=x_{1}-1-\ln x_{1}+x_{1}$ ． Il est donc nécessaire de déterminer la valeur de $x_{1}$ ． On a ：$f\left(x_{1}\right)=1$ ．Et par là ：$\frac{1}{x_{1}}-1=1$ ．Et donc ：$\frac{1}{x_{1}}=2$ ．D＇où ：$x_{1}=0,5$ ． Par conséquent ：$A_{t}=0,5-1-\ln 0,5+0,5=-\ln 0,5=-\ln \frac{1}{2}$ ． Soit ：$A_{t}=\ln 2$ ．

En procédant de façon similaire，on obtient ：

$$ A_{n}=\int_{0}^{x_{a}} a d x+\int_{x_{a}}^{1} f(x) d x $$

Soit ：$A_{n}=a x_{a}-1-\ln x_{a}+x_{a}$ ． Il est donc nécessaire de déterminer la valeur de $x_{a}$ ． On a：$f\left(x_{a}\right)=a$ ．Et par là ：$\frac{1}{x_{a}}-1=a$ ．Et donc ：$\frac{1}{x_{a}}=a+1$ ．D＇où ：$x_{a}=\frac{1}{a+1}$ ． Par conséquent ： $A_{n}=a \frac{1}{a+1}-1-\ln \frac{1}{a+1}+\frac{1}{a+1}=\frac{a-a-1+1}{a+1}-\ln \frac{1}{a+1}=-\ln \frac{1}{a+1}$. Soit ：$A_{n}=\ln (a+1)$

On résout donc ： $\ln 2=2 \ln (a+1)$ ． On obtient immédiatement ： $\ln (a+1)=\frac{1}{2} \ln 2$ ． Soit： $\ln (a+1)=\ln \sqrt{2}$ ． Et par là ：$a=\sqrt{2}-1 \approx 0,414$ ．

Exercice 9

A．Calculer $I_{1}=\int_{1}^{e} \ln (x) d x$ à l＇aide d＇une intégration par parties．

B．Dériver la fonction $\ln (1+x)$ ． Déterminer la valeur de $I_{2}=\int_{0}^{1} \frac{x}{1+x} d x$ (il est judicieux de remarquer que $\frac{x}{1+x}=\frac{1+x-1}{1+x}$ ) On pose $I_{3}=\int_{0}^{1} \ln (1+x) d x$. Montrer que $I_{3}=\ln \frac{4}{e}$ à l'aide d'une intégration par parties.

Corrigé

L'intégration par partie remplace le calcul de $\int_{a}^{b} u^{\prime} v d t$ par celui de $\int_{a}^{b} u v^{\prime} d t$. A. On pose : $u^{\prime}=1$ et $v=\ln (x)$.

Par conséquent : $u=x$ convient. Et de plus, on a : $v^{\prime}=\frac{1}{x}$. On obtient alors :

$$ I_{1}=\int_{1}^{e} \ln (x) d x=[x \times \ln (x)]{1}^{e}-\int{1}^{e} x \times \frac{1}{x} d x==[x \ln (x)]{1}^{e}-\int{1}^{e} 1 d x $$

Soit : $I_{1}=e \times \ln e-1 \times \ln 1-[x]{1}^{e}=e-0-(e-1)$. Soit: $I{1}=e-e+1$. Donc finalement: $I_{1}=1$. B. On sait que la dérivée de $\ln u$ vaut $\frac{u^{\prime}}{u}$.

Ici, $u=1+x$ et $u^{\prime}=1$. La dérivée de $\ln (1+x)$ est donc $\frac{1}{1+x}$. On a :

$$ I_{2}=\int_{0}^{1} \frac{x}{1+x} d x=\int_{0}^{1} \frac{1+x-1}{1+x} d x=\int_{0}^{1} \frac{1+x}{1+x} d x-\int_{0}^{1} \frac{1}{1+x} d x $$

Donc : $I_{2}=\int_{0}^{1} d x-\int_{0}^{1} \frac{1}{1+x} d x$. Donc : $I_{2}=[x]{0}^{1}-[\ln (1+x)]{0}^{1}$. Donc : $I_{2}=1-0-(\ln (2)-\ln (1))$. Donc: $I_{2}=1-\ln (2)$. On ne connaît pas de primitive de $\ln (1+x)$, mais on repère un produit caché. Une intégration par parties semble judicieuse. On pose : $u^{\prime}=1$ et $v=\ln (1+x)$. Par conséquent : $u=x$ convient. Et de plus, on a : $v^{\prime}=\frac{1}{1+x}$. On obtient alors :

$$ I_{3}=\int_{0}^{1} \ln (1+x) d x=[x \times \ln (1+x)]{0}^{1}-\int{0}^{1} x \times \frac{1}{1+x} d x $$

Soit : $\quad I_{3}=[x \ln (1+x)]{0}^{1}-\int{0}^{1} \frac{x}{1+x} d x$. Soit : $I_{3}=[x \ln (1+x)]{0}^{1}-I{2}$. Soit : $I_{3}=1 \times \ln 2-0 \times \ln 1-(1-\ln 2)=\ln 2-1+\ln 2$. Soit : $I_{3}=2 \ln 2-1=\ln 2^{2}-\ln e$. Donc finalement : $I_{3}=\ln \frac{4}{e}$.

Exercice 10

Dans cet exercice, toute trace de recherche, même non aboutie, serait prise en compte lors de la notation

Une fonction $f$, continue et positive sur $[0,2 ; 1]$, est représentée par la courbe C cidessous. On considère les points $A_{k}(0,2 k+0,2 ; 0)$ et $B_{k}(0,2 k+0,2 ; f(0,2 k+0,2))$, pour $k$ variant de 0 à 4 . 1.a. Soit $s$ l'aire du domaine limité par C , l'axe des abscisses, et les droites d'équations $x=0,2$ et $x=1$. On décide d'approcher $s$ par la somme des aires des trapèzes du type $A_{k} A_{k+1} B_{k+1} B_{k}$ On considère un programme associé à l'algorithme ci-dessous. $s \leftarrow 0$ Pour $k$ allant de ... à ... $s \leftarrow \ldots$ Fin du Pour Afficher ...

La fonction $f$ éventuellement citée dans l'algorithme est connue du programme. Expliquer pourquoi un trapèze du type $A_{k} A_{k+1} B_{k+1} B_{k}$ admet pour aire : $(f(0,2 k+0,2)+f(0,2 k+0,4)) \times 0,1$ Recopier et compléter l'algorithme ci-dessus pour qu'il affiche une estimation de l'aire $s$. 1.b. On considère la fonction $f$ définie par $f(x)=\left(2 x+x^{2}\right) e^{x}+0,5$ sur $[0,2 ; 1]$. Recopier et compléter le tableau de valeurs suivant :

$x$	0,2	0,4	0,6	0,8	1
$f(x)$	$\ldots$	$\ldots$	$\ldots$	$\ldots$	8,65

Les valeurs seront arrondies à 0,01 près. 1.c. Faire fonctionner l'algorithme pour la fonction $f$ ci-dessus. 1.d. Écrire en Python un programme correspondant à l'algorithme. 2.a. Montrer que la fonction $g$, définie par $g(x)=x^{2} e^{x}+0,5 x$ sur $[0,2 ; 1]$, est une primitive de $f$. 2.b. Déterminer la valeur exacte de l'aire $s$. 3. On décide d'approcher la longueur de l'arc de la courbe C allant de $B_{k}$ à $B_{k+1}$ par la longueur du segment $\left[B_{k} B_{k+1}\right]$. Ainsi, la longueur $l$ de la totalité de l'arc de la courbe C sur $[0,2 ; 1]$ sera approchée par la somme des longueurs des segments du type $\left[B_{k} B_{k+1}\right]$. Proposer un algorithme permettant d'estimer cette longueur $l$. Écrire en Python un programme correspondant à l'algorithme. Quel résultat s'affiche dans la console après exécution?

Corrigé

1.a. On rappelle qu'un trapèze admet pour aire $\frac{\text { base }+ \text { Base }}{2} \times$ hauteur.

Un trapèze du type $A_{k} A_{k+1} B_{k+1} B_{k}$ admet pour aire : $\frac{f(0,2 k+0,2)+f(0,2(k+1)+0,2)}{2} \times 0,2=(f(0,2 k+0,2)+f(0,2 k+0,4)) \times 0,1$ D'où l'algorithme suivant : $s \leftarrow 0$ Pour $k$ allant de 0 à 3

$$ s \leftarrow s+(f(0,2 k+0,2)+f(0,2 k+0,4)) \times 0,1 $$

Fin du Pour

Afficher $s$

La dernière valeur de $k$ est bien 3; on a alors $k+1=4$. Ne pas oublier le $s+\ldots$ car, à chaque itération, s augmente de l'aire d'un trapèze. 1.b.

$x$	0,2	0,4	0,6	0,8	1
$f(x)$	1,04	1,93	3,34	5,49	8,65

Les valeurs sont arrondies à 0,01 près. 1.c. $s=0$ $k=0$ (première boucle) $s=0+(f(0,2)+f(0,4)) \times 0,1 \approx 0+(1,04+1,93) \times 0,1 \approx 0,297$ $k=1$ (seconde boucle) $s \approx 0,297+(f(0,4)+f(0,6)) \times 0,1 \approx 0,297+(1,93+3,34) \times 0,1$ Soit : $s \approx 0,297+0,527 \approx 0,824$ $k=2$ (troisième boucle) $s \approx 0,824+(f(0,6)+f(0,8)) \times 0,1 \approx 0,824+(3,34+5,49) \times 0,1$ Soit : $s \approx 0,824+0,883 \approx 1,707$ $k=3$ (quatrième boucle) $s \approx 1,707+(f(0,8)+f(1)) \times 0,1 \approx 1,707+(5,49+8,65) \times 0,1$ Soit : $s \approx 1,707++1,414 \approx 3,121$ (il n'y a pas de cinquième boucle) Il s'affiche la valuer de $s$, c'est-à-dire environ 3,121 1.d. Voici un programme en Python correspondant à l'algorithme.

1 from math import* \# pour définir la fonction exp
$2 \operatorname{def} \mathrm{f}(\mathrm{x})$ : \# pour définir la fonction $f$
    $\mathrm{y}=\left(2^{*} \mathrm{x}+\mathrm{x}^{* *} 2\right) * \exp (\mathrm{x})+.5$
    return $y$
5
$6 s=0$
7 for $k$ in range(4):
    $s=s+(f(0.2 * k+0.2)+f(0.2 * k+0.4)) * 0.1$
9
0 print(s)

2.a. Pour tout $x$ de $[0,2 ; 1]$, on a : $g^{\prime}(x)=2 x e^{x}+x^{2} e^{x}+0,5=\left(2 x+x^{2}\right) e^{x}+0,5=f(x)$. Donc $g^{\prime}=f$ sur $[0,2 ; 1]$, et par là, $g$ est une primitive de $f$. 2.b. La fonction $f$ étant continue et positive sur $[0,2 ; 1]$, on en déduit que : $s=\int_{0,2}^{1} f(x) d x$. Donc : $s=g(1)-g(0,2)=e+0,5-\left(0,04 e^{0,2}+0,1\right)=e-0,04 e^{0,2}+0,4$. Notons que l'on obtient $s \approx 3,069$. La valeur trouvée est légèrement inférieure à celle produite par l'algorithme. Cela est conforme au graphique; en effet, le domaine des 4 trapèzes contient visiblement le domaine sous la courbe, car cette dernière est dite convexe. 3. On rappelle qu'un segment $[A B]$ a pour longueur $\sqrt{\left(x_{B}-x_{A}\right)^{2}+\left(y_{B}-y_{A}\right)^{2}}$

Un segment du type [ $B_{k} B_{k+1}$ ] admet donc pour longueur : $\sqrt{0,2^{2}+(f(0,2(k+1)+0,2)-f(0,2 k+0,2))^{2}}$ D'où l'algorithme suivant: $l \leftarrow 0$ Pour $k$ allant de 0 à 3

$$ l \leftarrow l+\sqrt{0,2^{2}+(f(0,2(k+1)+0,2)-f(0,2 k+0,2))^{2}} $$

Fin du Pour Afficher $l$

Voici un programme en Python correspondant à l'algorithme.

from math import* # pour définir les fonctions exp et sqrt
def f(x): # pour définir la fonction f
    y=(2*x+x**2)*exp(x)+.5
    return y
l=0
for k in range(4):
    l=l+sqrt(0.2**2+(f(0.2*(k+1)+0.2)-f(0.2*k+0.2))**2)
print(l)

Il s'affiche 7.669236429054836 dans la console après exécution ; c'est la longueur du polygone qui approche la portion de courbe.