Exercices : Représentations paramétriques et équations cartésiennes
Exercices corrigés
Exercice 1
L'espace est muni d'un repère (orthonormal si cela vous fait plaisir). Soit $d_{1}$ la droite passant par $\mathrm{A}(1,2,-1)$ et de vecteur directeur $\vec{u}(-1 ; 2 ; 0)$. Soit $d_{2}$ la droite passant $\operatorname{par} \mathrm{B}(2,0,0)$ et $\mathrm{C}(0,1,2)$. Soit $d_{3}$ la droite de représentation paramétrique $\left{\begin{array}{c}x=-2 t \ y=1+4 t \ z=2\end{array}\right.$ Soit $d_{4}$ la droite passant par $\mathrm{F}(3 ; 1 ;-2)$ et parallèle à $d_{1}$.
- Déterminer une équation paramétrique de $d_{1}$.
- Déterminer une équation paramétrique de $d_{2}$.
- Donner un point et un vecteur directeur de $d_{3}$.
- Déterminer une équation paramétrique de $d_{4}$.
- $d_{1}$ et $d_{2}$ sont-elles coplanaires ?
- $d_{1}$ et $d_{3}$ sont-elles coplanaires ?
- $d_{2}$ et $d_{4}$ sont-elles coplanaires ? Si oui, déterminer les coordonnées de leur point d'intersection E .
Corrigé
- $d_{1}$ passe par $\mathrm{A}(1 ; 2 ;-1)$ et a pour vecteur directeur $\vec{u}(-1 ; 2 ; 0)$, donc elle admet pour représentation paramétrique $\left{\begin{array}{c}x=1-t \ y=2+2 t \ z=-1\end{array}\right.$
- On obtient facilement : $\overrightarrow{B C}(-2 ; 1 ; 2)$. $d_{2}$ passe par $\mathrm{B}(2 ; 0 ; 0)$ et a pour vecteur directeur $\overrightarrow{B C}(-2 ; 1 ; 2)$, Donc elle admet pour représentation paramétrique $\left{\begin{array}{c}x=2-2 t \ y=t \ z=2 t\end{array}\right.$
- $d_{3}$ a pour représentation paramétrique $\left{\begin{array}{c}x=-2 t \ y=1+4 t \ z=2\end{array}\right.$
Donc $d_{3}$ passe par $\mathrm{E}(0 ; 1 ; 2)$ et elle a pour vecteur directeur $\vec{w}(-2 ; 4 ; 0)$. 4. $d_{1}$ a pour vecteur directeur $\vec{u}(-1 ; 2 ; 0)$.
Or $d_{4}$ est parallèle à $d_{1}$. Donc $d_{4}$ a aussi pour vecteur directeur $\vec{u}(-1 ; 2 ; 0)$. Or $d_{4}$ passe par $\mathrm{F}(3 ; 1 ;-2)$. Donc elle admet pour représentation paramétrique $\left{\begin{array}{c}x=3-t \ y=1+2 t \ z=-2\end{array}\right.$ 5. $d_{1}$ et $d_{2}$ ont des vecteurs directeurs $\vec{u}(-1 ; 2 ; 0)$ et $\overrightarrow{B C}(-2 ; 1 ; 2)$ qui ne sont pas colinéaires (leurs coordonnées ne sont pas proportionnelles). Donc elles ne sont pas parallèles. Donc ces droites sont : soit non coplanaires, soit coplanaires et sécantes. Or, les coordonnées d'un point appartenant aux deux droites vérifient les deux équations paramétriques. On résout alors : $\left{\begin{array}{c}1-t=2-2 t^{\prime} \ 2+2 t=t^{\prime} \ -1=2 t^{\prime}\end{array}\right.$ On note les paramètres portant des noms différents $t$ et $t^{\prime}$ (car il n'y a pas de raison qu'ils soient égaux). On cherche ici un couple ( $t, t^{\prime}$ ) solution du système. On obtient: $\left{\begin{array}{c}1-t=2-2 t^{\prime} \ 2+2 t=t^{\prime} \ t^{\prime}=-0.5\end{array}\right.$
Soit : $\left{\begin{array}{c}1-t=3 \ 2+2 t=-0.5 \ t^{\prime}=-0.5\end{array}\right.$ Soit : $\left{\begin{array}{c}t=-2 \ t=-1.25 \ t^{\prime}=-0.5\end{array}\right.$ Les deux premières égalités sont absurdes. Donc le système n'a pas de solution. Donc $d_{1}$ et $d_{2}$ n'ont pas de point commun. Par conséquent, $d_{1}$ et $d_{2}$ ne sont pas coplanaires. 6. $d_{1}$ et $d_{3}$ ont des vecteurs directeurs $\vec{u}(-1 ; 2 ; 0)$ et $\vec{w}(-2 ; 4 ; 0)$ qui sont colinéaires ( $\vec{u}=2 \cdot \vec{w}$ ). Donc $d_{1}$ et $d_{3}$ sont parallèles. Par conséquent, $d_{1}$ et $d_{3}$ sont coplanaires. 7. $d_{2}$ et $d_{4}$ ont des vecteurs directeurs $\overrightarrow{B C}(-2 ; 1 ; 2)$ et $\vec{u}(-1 ; 2 ; 0)$. qui ne sont pas colinéaires (leurs coordonnées ne sont pas proportionnelles). Donc elles ne sont pas parallèles. Donc ces droites sont soit non coplanaires, soit coplanaires et sécantes. On résout alors : $\left{\begin{array}{c}2-2 t=3-t^{\prime} \ t=1+2 t^{\prime} \ 2 t=-2\end{array}\right.$ Soit : $\left{\begin{array}{c}2-2 t=3-t^{\prime} \ t=1+2 t^{\prime} \ t=-1\end{array}\right.$ Soit : $\left{\begin{array}{c}4=3-t^{\prime} \ -1=1+2 t^{\prime} \ t=-1\end{array}\right.$ Soit : $\left{\begin{array}{l}t^{\prime}=-1 \ t^{\prime}=-1 \ t=-1\end{array}\right.$ On note les paramètres $t$ et $t^{\prime}$ sont ici égaux. Ce cas est rare. On constate que le système a une solution unique, le couple ( $-1 ;-1$ ). Donc $d_{1}$ et $d_{2}$ sont sécantes. Par conséquent, $d_{1}$ et $d_{2}$ sont coplanaires.
En prenant $t=-1$ dans l'équation paramétrique de $d_{2}$, on obtient : $\left{\begin{array}{c}x=4 \ y=-1 \ z=-2\end{array}\right.$ Donc $d_{1}$ et $d_{2}$ se coupent en $\mathrm{E}(4 ;-1 ;-2)$
Exercice 2
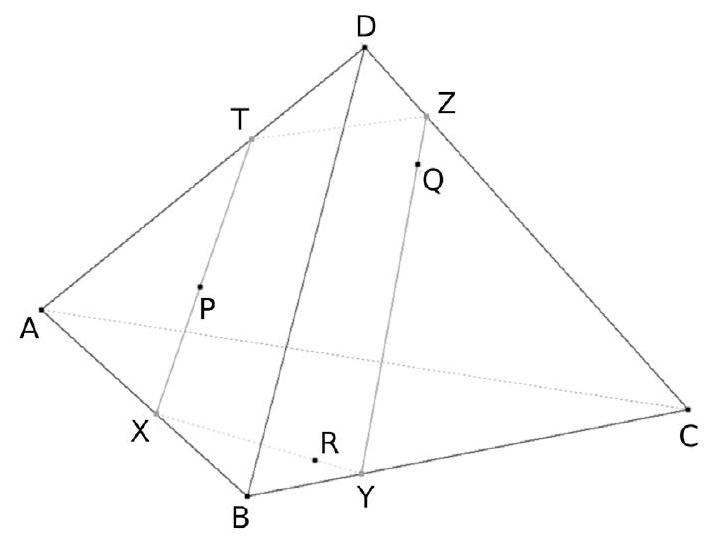
Un décorateur veut tendre une toile plane dans un édifice en forme de tétraèdre. Pour des raisons esthéthiques, il veut absolument que cette toile affleure 3 points P , Q et R qu'il a placés sur certaines faces de l'édifice. Le tétraèdre ABCD est dessiné ci-après. Le point $P$ est sur la face $A B D$. Le point Q est sur la face BCD . Le point R est sur la face ABC .
Figure 1.
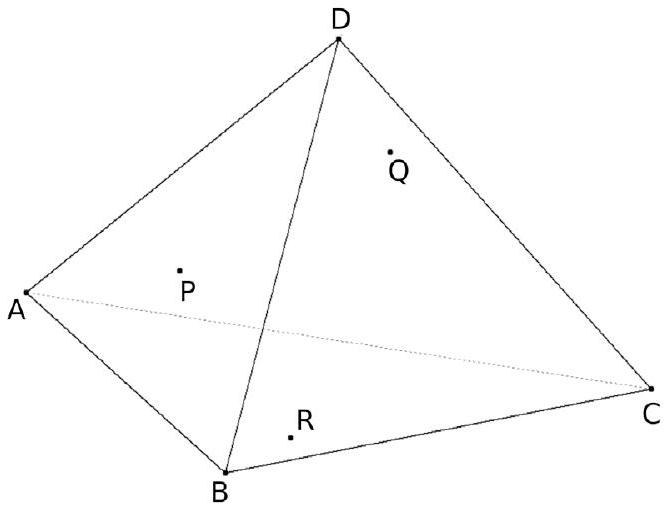
La section du tétraèdre ABCD par le plan $(\mathrm{PQR})$ est le quadrilatère XYZT.
Le décorateur recherche les positions exactes des points $\mathrm{X}, \mathrm{Y}, \mathrm{Z}$ et T .
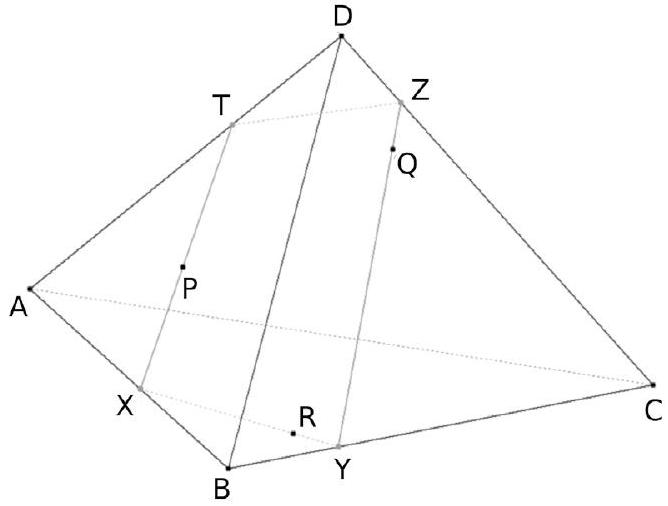
Dans tout ce qui suit, les points $A, B, C, D, P, Q, R, X, Y$ et $Z$ sont supposés distincts deux à deux.
Partie A
Nous allons déterminer la section XYZT par des constructions géométriques. Reproduire la figure 1 (sans la section), et la compléter au fur et à mesure. Soit $M$ le point d'intersection de la droite (DP) avec la droite (AB). Soit N le point d'intersection de la droite (DQ) avec la droite (BC).
- Pourquoi les droites $(\mathrm{MN})$ et $(\mathrm{PQ})$ sont-elles coplanaires ?
- Soit K le point d'intersection des droites ( MN ) et ( PQ ).
On admet que les plans $(\mathrm{PQR})$ et $(\mathrm{ABC})$ sont sécants. Donner 2 points appartenant à l'intersection du plan ( PQR ) et du plan ( ABC ). 3. Déterminer graphiquement les points X et Y , puis terminer la section.
Partie B
Nous allons retrouver la section XYZT par des constructions analytiques. On se place dans un repère du plan (orthonormal si cela vous fait plaisir) tel que les points $\mathrm{A}, \mathrm{B}, \mathrm{C}$ et D aient les coordonnées suivantes. $\mathrm{A}(0 ;-2 ; 0) \mathrm{B}(2 ; 0 ; 0) \mathrm{C}(0 ; 2 ; 0) \mathrm{D}(0 ; 0 ; 2)$. Par ailleurs, les points $\mathrm{P}, \mathrm{Q}$ et R ont les coordonnées suivantes. $\mathrm{P}(0,6 ;-0,8 ; 0,6) \mathrm{Q}(0,2 ; 0,4 ; 1,4) \mathrm{R}(1,4 ; 0,2 ; 0)$
- Déterminer les coordonnées des vecteurs $\overrightarrow{P Q}$ et $\overrightarrow{P R}$.
Montrer que, tout point $M(x ; y ; z)$ appartient au plan (PQR) si et seulement si il existe deux réels $t$ et $t^{\prime}$ tels que :
$$ \left{\begin{array}{c} x=0.6-0.4 t+0.8 t^{\prime} \ y=-0.8+1.2 t+t^{\prime} \ z=0.6+0.8 t-0.6 t^{\prime} \end{array}\right. $$
On dit alors que le plan $(\mathrm{PQR})$ admet pour représentation paramétrique :
$$ \left{\begin{array}{c} x=0.6-0.4 t+0.8 t^{\prime} \ y=-0.8+1.2 t+t^{\prime} \ z=0.6+0.8 t-0.6 t^{\prime} \end{array}\right. $$
- On admet que le plan $(\mathrm{ABC})$ admet pour représentation paramétrique :
$$ \left{\begin{array}{c} x=2 a \ y=-2+2 a+4 b \ z=0 \end{array}\right. $$
Vérifier que $R$ est bien dans le plan (ABC). 3. Soit $d$ la droite admettant pour représentation paramétrique $\left{\begin{array}{c}x=1.4+\frac{2}{3} t \ y=0.2+\frac{7.6}{3} t \ z=0\end{array}\right.$
On admet que les plans $(\mathrm{PQR})$ et $(\mathrm{ABC})$ sont sécants. Montrer que les plans (PQR) et (ABC) se coupent selon la droite $d$. 4. Déterminer les coordonnées ( $e ; f ; g$ ) du point X , intersection de la droite $d$ avec la droite $(\mathrm{AB})$. Ces coordonnées seront arrondies à 0,01 près. On pourrait de même déterminer les coordonnées des points $Y, Z$ et $T$.
Corrigé
Partie A
- $M$ est le point d'intersection de la droite ( DP ) avec la droite ( AB ), donc il est sur (DP), et donc dans le plan (DPQ).
N est le point d'intersection de la droite ( DQ ) avec la droite ( BC ), donc il est sur (DQ), et donc dans le plan (DPQ).
M et N étant dans le plan (DPQ), la droite (MN) est donc dans le plan (DPQ).
Or la droite (PQ) est évidemment dans le plan (DPQ).
Donc les droites (MN) et (PQ) sont toutes deux dans le plan (DPQ) ; elles sont donc coplanaires.
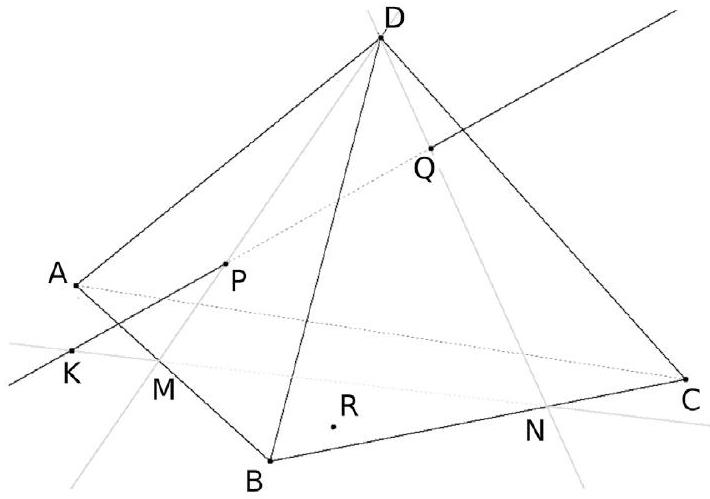
- Comme M est sur la droite ( AB ), il est donc dans le plan ( ABC ). De même, il est clair que N est également dans ( ABC ). Donc la droite ( MN ) est incluse dans ( ABC ). Et comme $K$ est sur $(\mathrm{MN}), \mathrm{K}$ est donc dans le plan ( ABC ). Par ailleurs, comme $K$ est dans $(\mathrm{PQ})$, il est dans le plan (PQR). Donc finalement K appartient à l'intersection des plans ( ABC ) et ( PQR ).
Par ailleurs, R est, par hypothèse, dans le plan ( ABC ), et il est également évidemment dans le plan (PQR).
Donc R appartient à l'intersection des plans ( ABC ) et ( PQR ).
L'intersection des plans ( ABC ) et ( PQR ) contient donc les points K et R .
3. Comme les plans $(\mathrm{PQR})$ et $(\mathrm{ABC})$ sont sécants, d'après ce qui précède, ils se coupent selon la droite (KR).
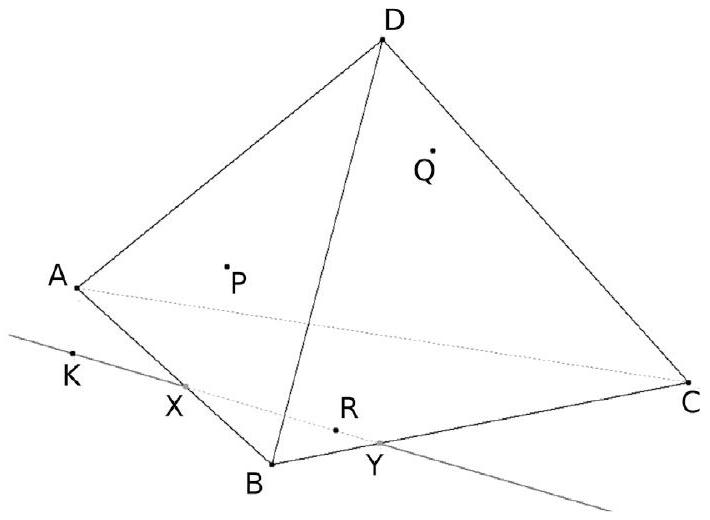
Le point $X$ est alors à l'intersection de ( KR ) et de ( AB ). Le point Y est alors à l'intersection de (KR) et de (BC). La section s'obtient en traçant [XY], puis en traçant [XT], où T est à l'intersection de ( XP ) et de ( AD ), puis en traçant [ YZ ], où Z est à l'intersection de (YQ) et de (DC).
Elle se termine en traçant [TZ].
Partie B
- On obtient facilement: $\overrightarrow{P Q}(-0,4 ; 1,2 ; 0,8)$ et $\overrightarrow{P R}(0,8 ; 1 ;-0,6)$.
Ces deux vecteurs, non colinéaires (ils sont non nuls et leurs coordonnées ne sont pas proportionnelles), forment une base du plan vectoriel (PQR).
Comme P appartient à ( PQR ), M est sur ( PQR ) si et seulement si il existe deux réels $t$ et $t^{\prime}$ tels que $\overrightarrow{P M}=t \cdot \overrightarrow{P Q}+t^{\prime} \cdot \overrightarrow{P R}$. Soit : $\left{\begin{array}{c}x-0 \quad 6=-0.4 t+0.8 t^{\prime} \ y+0.8=1.2 t+t^{\prime} \ z-0.6=0.8 t-0.6 t^{\prime}\end{array}\right.$ Soit : $\left{\begin{array}{c}x=0.6-0.4 t+0.8 t^{\prime} \ y=-0.8+1.2 t+t^{\prime} \ z=0.6+0.8 t-0.6 t^{\prime}\end{array}\right.$ Donc le plan $(\mathrm{PQR})$ a bien pour représentation paramétrique : $\left{\begin{array}{c}x=0.6-0.4 t+0.8 t^{\prime} \ y=-0.8+1.2 t+t^{\prime} \ z=0.6+0.8 t-0.6 t^{\prime}\end{array}\right.$ 2. Le plan (ABC) admet pour représentation paramétrique $\left{\begin{array}{c}x=2 a \ y=-2+2 a+4 b \ z=0\end{array}\right.$
Or on $\mathrm{a}: \mathrm{R}(1,4 ; 0,2 ; 0)$. On résout donc $:\left{\begin{array}{c}1.4=2 a \ 0.2=-2+2 a+4 b \ 0=0\end{array}\right.$ $\left{\begin{array}{c}0.7=a \ 0.2=-2+2 \times 0.7+4 b\end{array}\right.$ $\left{\begin{array}{l}a=0.7 \ b=0.2\end{array}\right.$ Le système admet un couple solution, ce qui prouve que R est bien dans le plan (ABC). 3. Le plan $(\mathrm{ABC})$ admet pour représentation paramétrique $\left{\begin{array}{c}x=2 a \ y=-2+2 a+4 b \ z=0\end{array}\right.$
Or le plan $(\mathrm{PQR})$ a pour représentation paramétrique $\left{\begin{array}{l}x=0.6-0.4 t+0.8 t^{\prime} \ y=-0.8+1.2 t+t^{\prime} \ z=0.6+0.8 t-0.6 t^{\prime}\end{array}\right.$ On résout donc : $\left{\begin{array}{c}x=2 a=0.6-0.4 t+0.8 t^{\prime} \ y=-2+2 a+4 b=-0.8+1.2 t+t^{\prime} \ z=0=0.6+0.8 t-0.6 t^{\prime}\end{array}\right.$ La dernière ligne donne immédiatement : $t^{\prime}=1+\frac{4}{3} t$.
La première ligne donne alors : $x=2 a=0.6-0.4 t+0.8\left(1+\frac{4}{3} t\right)=1.4+\frac{2}{3} t$ Et enfin, la seconde ligne donne : $y=-2+2 a+4 b=-0.8+1.2 t+1+\frac{4}{3} t=0.2+\frac{7.6}{3} t$ Et par là, les plans $(\mathrm{PQR})$ et $(\mathrm{ABC})$ se coupent selon la droite d'équation paramétrique : $\left{\begin{array}{c}x=1.4+\frac{2}{3} t \ y=0.2+\frac{7.6}{3} t \ z=0\end{array}\right.$ Il s'agit bien de la droite $d$. 4. On obtient : $\overrightarrow{A B}(2 ; 2 ; 0)$. Et comme on a : A( $0 ;-2 ; 0$ ), la droite (AB) a pour représentation paramétrique $\left{\begin{array}{c}x=2 a \ y=-2+2 a \ z=0\end{array}\right.$ On résout donc : $\left{\begin{array}{c}x=2 a=1.4+\frac{2}{3} t \ y=-2+2 a=0.2+\frac{7.6}{3} t \ z=0=0\end{array}\right.$ La première ligne et la seconde donnent : $-2+1,4+\frac{2}{3} t=0,2+\frac{7,6}{3} t$ Et par là : $t=-\frac{2,4}{5,6}$. Et donc finalement : $\left{\begin{array}{c}x=1.4+\frac{2}{3} \times\left(-\frac{2.4}{5.6}\right) \approx 1.11 \ y=0.2+\frac{7.6}{3} \times\left(-\frac{2.4}{5.6}\right) \approx-0.89 \ z=0=0\end{array}\right.$ Donc : $e \approx 1,11, f \approx-0,89$ et $g=0$. On pourrait de même déterminer les coordonnées des points $Y, Z$ et $T$.
Exercice 3
L'espace est muni d'un repère orthonormal. Soit P le plan d'équation $-3 x+3 y-5 z+3=0$. Soient $\vec{u}(1 ; 0 ; 1)$ et $\vec{v}(2 ; 3 ; 0)$ deux vecteurs. Soit Q le plan passant $\operatorname{par} \mathrm{B}(1,2,3)$ de vecteurs directeurs $\vec{u}$ et $\vec{v}$. Soit $d$ la droite passant par $\mathrm{C}(-12,-13,0)$ et de vecteur directeur $\vec{w}(19 ; 24 ; 3)$.
- Montrer que $3 x-2 y-3 z+10=0$ est une équation cartésienne de Q .
- Montrer que P et Q sont perpendiculaires.
3.Montrer que P et Q se coupent selon la droite $d$ . 4.Déterminer une équation cartésienne du plan R passant par C et orthogonal à $d$ .
Corrigé
L'espace est muni d'un repère orthonormal,ce qui autorise tous calculs de distances, normes ou produits scalaires. 1.Méthode 1 : Q passe par $\mathrm{B}(1,2,3)$ et a pour vecteurs directeurs $\vec{u}(1 ; 0 ; 1)$ et $\vec{v}(2 ; 3 ; 0)$ . Donc $Q$ admet pour représentation paramétrique $\left{\begin{array}{c}x=1+t+2 t^{\prime} \ y=2+3 t^{\prime} \ z=3+t\end{array}\right.$ Or $\left{\begin{array}{c}x=1+t+2 t^{\prime} \ y=2+3 t^{\prime} \ z=3+t\end{array} \Leftrightarrow\left{\begin{array}{c}x=1+t+2 t^{\prime} \ \frac{y-2}{3}=t^{\prime} \ z-3=t\end{array} \Leftrightarrow\left{\begin{array}{c}x=1+z-3+\frac{2(y-2)}{3} \ y=2+3 t^{\prime} \ z=3+t\end{array}\right.\right.\right.$ La première ligne équivaut à : $3 x=3+3 z-9+2 y-4$ . soit : $3 x-2 y-3 z+10=0$ ,qui est donc bien une équation cartésienne de Q .
Méthode 2 :
Appelons Q'le plan d'équation cartésienne $3 x-2 y-3 z+10=0$ ,et montrons que Q et Q'sont confondus. Q'a pour vecteur normal $\overrightarrow{n^{\prime}}(3 ;-2 ;-3)$ . Par ailleurs,Q a pour vecteurs directeurs $\vec{u}(1 ; 0 ; 1)$ et $\vec{v}(2 ; 3 ; 0)$ . Or $\vec{u} \cdot \overrightarrow{n^{\prime}}=1 \times 3+0 \times(-2)+1 \times(-3)=0$ . et $\vec{v} \cdot \overrightarrow{n^{\prime}}=2 \times 3+3 \times(-2)+0 \times(-3)=0$ . Donc $\overrightarrow{n^{\prime}}$ est un vecteur normal au plan Q . De plus,comme $3 x_{C}-2 y_{C}-3 z_{C}+10=3 \times(-12)-2 \times(-13)-3 \times 0+10=0$ ,le point C est sur Q'. Finalement,Q'et Q ont un même vecteur normal et passent tous les deux par le même point C . Ils sont donc confondus. Donc $3 x-2 y-3 z+10=0$ est bien une équation cartésienne de Q .
2.Au vu des équations cartésiennes,on en déduit que: P admet pour vecteur normal :$\vec{n}(-3 ; 3 ;-5)$ .
Q admet pour vecteur normal : $\overrightarrow{n^{\prime}}(3 ;-2 ;-3)$. On a alors: $\vec{n} \cdot \overrightarrow{n^{\prime}}=-3 \times 3+3 \times(-2)+(-5) \times(-3)=-9-6+15=0$. Les vecteurs normaux sont donc orthogonaux, et par là, les plans $P$ et $Q$ sont perpendiculaires . 3. Les plans P et Q , orthogonaux, sont donc sécants selon une droite.
Méthode 1 : Pour montrer que P et Q se coupent selon $d$, il suffit de trouver 2 points distincts de $d$ appartenant à la fois à P et à Q . Considérons le point C . $-3 x_{C}+3 y_{C}-5 z_{C}+3=-3 \times(-12)+3 \times(-13)-5 \times 0+3=0$. Donc C est sur P . $3 x_{C}-2 y_{C}-3 z_{C}+10=3 \times(-12)-2 \times(-13)-3 \times 0+10=0$. Donc C est sur Q.
Pour trouver un second point E de $d$, il suffit de déterminer une équation paramétrique de $d$. $d$ passe par $\mathrm{C}(-12,-13,0)$ et a pour vecteur directeur $\vec{w}(19 ; 24 ; 3)$. Elle admet donc pour représentation paramétrique $\left{\begin{array}{c}x=-12+19 t \ y=-13+24 t \ z=3 t\end{array}\right.$ $t=1$ nous donne le point $\mathrm{E}(7 ; 11 ; 3)$ sur la droite $d$. $-3 x_{E}+3 y_{E}-5 z_{E}+3=-3 \times 7+3 \times 11-5 \times 3+3=0$. Donc E est sur P. $3 x_{E}-2 y_{E}-3 z_{E}+10=3 \times 7-2 \times 11-3 \times 3+10=0$. Donc E est sur Q. Finalement, P et Q se coupent selon la droite (CE), c'est-à-dire $d$.
Méthode 2 :
$d$ passe par $\mathrm{C}(-12,-13,0)$ et a pour vecteur directeur $\vec{w}(19 ; 24 ; 3)$. Pour montrer que P et Q se coupent selon $d$, il suffit de montrer que $d$ est incluse dans chacun des 2 plans. On a: $-3 x_{C}+3 y_{C}-5 z_{C}+3=-3 \times(-12)+3 \times(-13)-5 \times 0+3=0$. Donc C est sur P . De plus, $\vec{n} \cdot \vec{w}=-3 \times 19+3 \times 24+(-5) \times 3=0$, où $\vec{n}$ est normal à P . Donc la droite $d$ est dans P . $3 x_{C}-2 y_{C}-3 z_{C}+10=3 \times(-12)-2 \times(-13)-3 \times 0+10=0$. Donc C est sur Q . De plus, $\vec{w} \cdot \overrightarrow{n^{\prime}}=19 \times 3+24 \times(-2)+3 \times(-3)=0$, où $\overrightarrow{n^{\prime}}$ est normal à Q . Donc la droite $d$ est dans Q . 4. Le plan R , passant par C et orthogonal à $d$, est tel que : $M(x ; y)$ est dans R si et seulement si $\overrightarrow{C N} \cdot \vec{w}=0$. Soit : $(x+12) \times 19+(y+13) \times 24+z \times 3=0$. Soit : $19 x+24 y+3 z+540=0$. Ce qui est donc une équation cartésienne de R .
Exercice 4
L'espace est muni du repère orthonormal ( $\mathrm{A}, \mathrm{B}, \mathrm{D}, \mathrm{K}$ ).
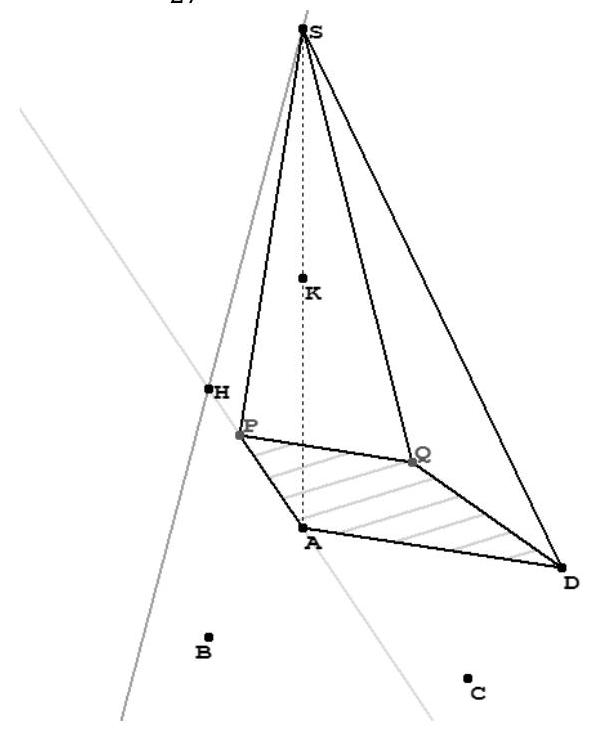
ABCDS est une pyramide à base carrée ABCD , telle que :
S a pour coordonnées $(0 ; 0 ; 2)$ et C a pour coordonnées $(1 ; 1 ; 0)$.
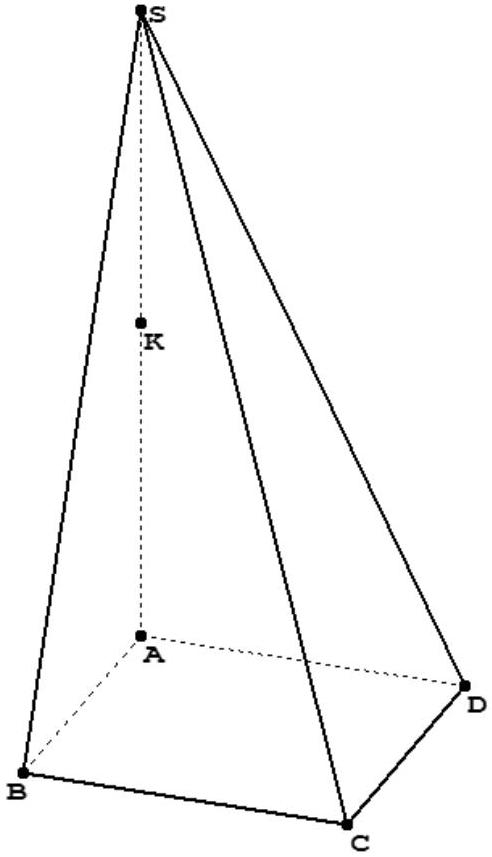
- Soit P le point de la droite $(\mathrm{SB})$ de $\operatorname{cote} \frac{2}{3}$. Construire le point P sur la figure.
- Soit Q le point d'intersection du plan (APD) et de la droite (SC).
Expliquer pourquoi (APD) et (BPC) se coupent selon la droite (PQ). On admettra que les droites $(\mathrm{AD})$ et $(\mathrm{PQ})$ sont parallèles. Construire le point Q sur la figure. 3. On admet que C a pour coordonnées ( $1 ; 1 ; 0$ ). et que P a pour coordonnées $\left(\frac{2}{3} ; 0 ; \frac{2}{3}\right)$. Déterminer une représentation paramétrique de la droite ( SC ). Déterminer une représentation paramétrique de la droite $(\mathrm{PQ})$.
Montrer que Q a pour coordonnées $\left(\frac{2}{3} ; \frac{2}{3} ; \frac{2}{3}\right)$. 4. Sans calcul, expliquer pourquoi le trapèze APQD a pour hauteur AP . Montrer que l'aire $s$ du trapèze APQD vaut $\frac{5}{9} \sqrt{2}$. 5. Déterminer une équation cartésienne du plan (APD), ainsi qu'une représentation paramétrique de la droite $d$ orthogonale à ce plan et passant par S . 6. Déterminer les coordonnées du point H , pied de la hauteur $(\mathrm{SH})$ de la pyramide PQDAS issue de S . 7. Déterminer le volume de la pyramide PQDAS.
Corrigé
L'espace est muni d'un repère orthonormal, ce qui autorise tous calculs de distances, normes ou produits scalaires.
- P est sur la droite $(\mathrm{SB})$. Or la droite $(\mathrm{SB})$ est dans le plan $(\mathrm{ABS})$. Donc le point P a pour ordonnée 0 . Comme sa cote est $\frac{2}{3}$, il suffit de partir de A , de monter de $\frac{2}{3}$ selon l'axe (AS). On arrive alors à un point T sur la figure. On trace alors une parallèle à la droite (AB). Elle coupe (BS) en P.
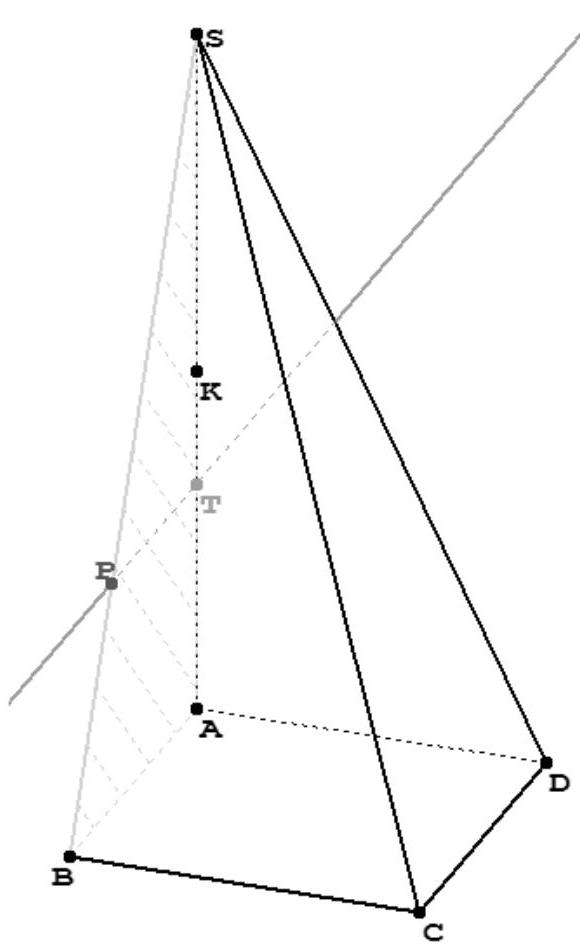
- $Q$ est le point d'intersection du plan (APD) et de la droite (SC).
Q appartient donc au plan (APD). Et il appartient aussi à la droite ( SC ). Et comme ( SC ) est clairement dans le plan (BPC), le point Q appartient donc au plan (BPC). Q appartient donc à la fois au plan (APD) et au plan (BPC). Or, P appartient aussi à ces 2 plans (c'est évident). Donc (APD) et (BPC) se coupent selon la droite (PQ).
On a admis que cette droite $(\mathrm{PQ})$ est parallèle à $(\mathrm{AD})$.
Cela permet de construire le point Q .
 3. On obtient facilement : $\overrightarrow{S C}(1 ; 1 ;-2)$.
3. On obtient facilement : $\overrightarrow{S C}(1 ; 1 ;-2)$.
Or C a pour coordonnées $(1 ; 1 ; 0)$. Donc la droite (SC) admet pour représentation paramétrique $\left{\begin{array}{l}x=1+t \ y=1+t \ z=-2 t\end{array}\right.$ Par ailleurs, P a pour coordonnées $\left(\frac{2}{3} ; 0 ; \frac{2}{3}\right)$. Or (AD) et (PQ) sont parallèles, et on a facilement : $\overrightarrow{A D}(0 ; 1 ; 0)$. Donc la droite $(\mathrm{PQ})$ admet pour représentation paramétrique $\left{\begin{array}{l}x=\frac{2}{3} \ y=t^{\prime} \ z=\frac{2}{3}\end{array}\right.$
Les coordonnées de Q qui appartient aux 2 droites vérifient les 2 représentations paramétriques : Donc : $\left{\begin{array}{l}\frac{2}{3}=1+t \ t^{\prime}=1+t \ \frac{2}{3}=-2 t\end{array}\right.$ Et par là : $\left{\begin{array}{c}-\frac{1}{3}=t \ t^{\prime}=\frac{2}{3} \ -\frac{1}{3}=t\end{array}\right.$ En reportant $t=-\frac{1}{3}$ dans la représentation paramétrique de (SC), on obtient : $\mathrm{Q}\left(\frac{2}{3} ; \frac{2}{3} ; \frac{2}{3}\right)$. 4. Comme les droites $(\mathrm{AD})$ et $(\mathrm{PQ})$ sont parallèles, les bases du trapèze APQD sont AD et PQ . Montrons que sa hauteur est AP .
La droite (AP) appartient clairement au plan (ABK). Or, comme (A, $\overrightarrow{A B}, \overrightarrow{A D}, \overrightarrow{A K}$ ) est un repère orthonormal, le plan (ABK) est orthogonal à la droite $(\mathrm{AD})$. Donc la droite $(\mathrm{AP})$ est orthogonale à la droite $(\mathrm{AD})$. Et par là, AP est bien la hauteur du trapèze APQD .
Reste à calculer toutes ces distances pour obtenir l'aire cherchée. On obtient facilement : $\overrightarrow{A D}(0 ; 1 ; 0), \overrightarrow{P Q}\left(0 ; \frac{2}{3} ; 0\right), \overrightarrow{A P}\left(\frac{2}{3} ; 0 ; \frac{2}{3}\right)$. D'où : $A D=\sqrt{0^{2}+1^{2}+0^{2}}=1$, et de même : $P Q=\frac{2}{3}$, et $A P=\frac{2}{3} \sqrt{2}$. D'où l'aire cherchée : $s=\frac{A D+P Q}{2} \times A P=\frac{1+\frac{2}{3}}{2} \times \frac{2}{3} \sqrt{2}=\frac{\frac{5}{3}}{2} \times \frac{2}{3} \sqrt{2}=\frac{5}{9} \sqrt{2}$ 5. (APD) passe par $\mathrm{A}(0,0,0)$.
Or il a pour vecteurs directeurs $\overrightarrow{A D}(0 ; 1 ; 0)$ et $\overrightarrow{A P}\left(\frac{2}{3} ; 0 ; \frac{2}{3}\right)$. Donc (APD) admet pour représentation paramétrique $\left{\begin{array}{c}x=\frac{2}{3} t^{\prime} \ y=t \ z=\frac{2}{3} t^{\prime}\end{array}\right.$
Or $\left{\begin{array}{c}x=\frac{2}{3} t^{\prime} \ y=t \ z=\frac{2}{3} t^{\prime}\end{array} \Leftrightarrow\left{\begin{array}{c}x=\frac{2}{3} t^{\prime} \ y=t \ \frac{3}{2} z=t^{\prime}\end{array} \Leftrightarrow\left{\begin{array}{c}x=\frac{2}{3} \times \frac{3}{2} z \ y=t \ \frac{3}{2} z=t^{\prime}\end{array}\right.\right.\right.$ La première ligne équivaut à : $x-z=0$, qui est une équation cartésienne de (APD).
Le plan (APD), d'équation cartésienne $x-z=0$, admet donc pour vecteur normal le vecteur $\vec{n}(1 ; 0 ;-1)$.
Et, comme $d$ est orthogonale à (APD), ce vecteur est un vecteur directeur de $d$.
Or $d$ passe par $\mathrm{S}(0 ; 0 ; 2)$.
Donc la droite $d$ admet pour représentation paramétrique $\left{\begin{array}{c}x=t \ y=0 \ z=2-t\end{array}\right.$
6. Remarque : l'angle droit en $H$ est déformé à cause de la perspective cavalière !
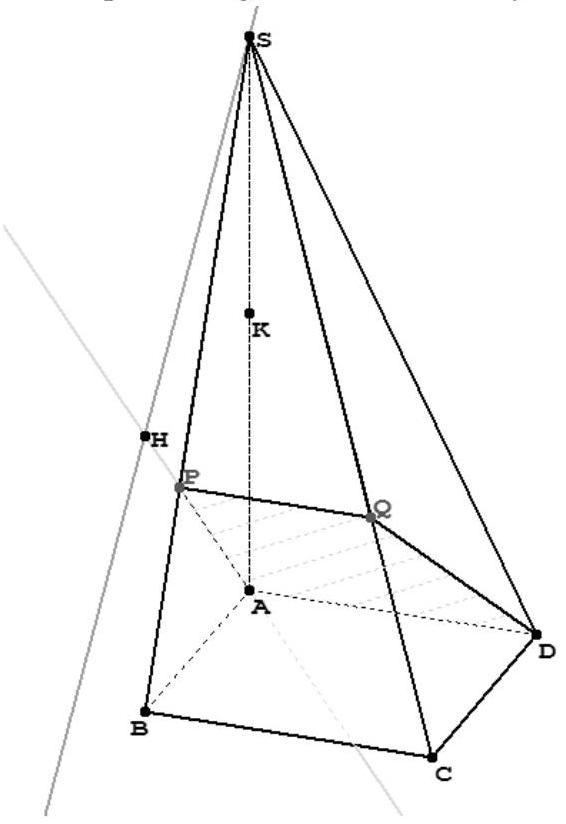
Le point H est le pied de la hauteur ( SH ) de la pyramide PQDAS issue de S . Donc H appartient au plan (APD) et à la droite orthogonale à ce plan qui passe par S , c'est-à-dire $d$. Donc, si H a pour coordonnées $(x, y, z)$, on a : $x-z=0$, et de plus, il existe un réel $t$ tel que $\left{\begin{array}{c}x=t \ y=0 \ z=2-t\end{array}\right.$
D'où : $t-(2-t)=0$, et par là : $t=1$. Par conséquent : $\left{\begin{array}{l}x=1 \ y=0 \ z=1\end{array}\right.$ Donc $\mathrm{H}(1 ; 0 ; 1)$. 7. Il est clair que la pyramide PQDAS a pour base APQD et pour hauteur HS .
Son volume est donc : $v=\frac{1}{3} \times s \times H S$.
Soit : $v=\frac{1}{3} \times \frac{5}{9} \sqrt{2} \times \sqrt{(0-1)^{2}+(0-0)^{2}+(2-1)^{2}}=\frac{5}{27} \sqrt{2} \times \sqrt{2}$.
Soit : $v=\frac{10}{27}$.
Exercice 5
L'espace est muni du repère orthonormal (A, I, J, K).
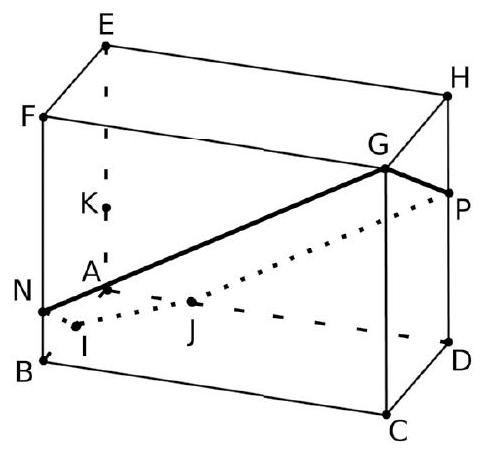
ABCDEFGH est un parallélépipède rectangle, tel que
B a pour coordonnées ( $2 ; 0 ; 0$ ), C a pour coordonnées ( $2 ; 4 ; 0$ ), E a pour coordonnées ( $0 ; 0 ; 3$ ) et F a pour coordonnées ( $2 ; 0 ; 3$ ).
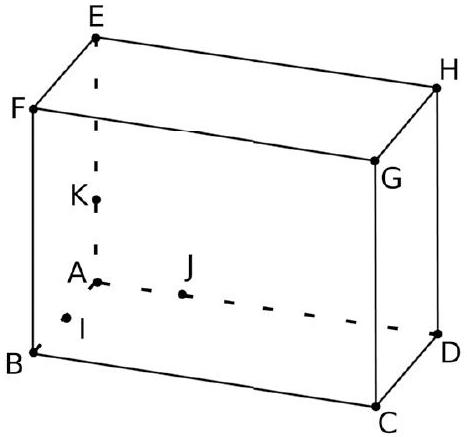
On considère le point N , intersection du plan (IJG) et de la droite (BF).
- Cette question ne nécessite aucun calcul
- Donner, sans justifier, un plan auquel appartiennent les droites (IJ) et (BC).
- On admettra que les droites (IJ) et (BC), coplanaires, sont sécantes en un point M.
Déterminer, en justifiant, la droite qui constitue l'intersection du plan (IJG) et du plan (BCG).
- Construire, sans justifier, le point N .
- Nous allons vérifier que la construction de $N$ est correcte en déterminant les coordonnées de $N$.
- Il est clair que G a pour coordonnées ( $2 ; 4 ; 3$ ).
Par ailleurs, le plan (IJG) admet pour vecteurs directeurs $\overrightarrow{I J}$ et $\overrightarrow{I G}$. Montrer que le vecteur $\vec{n}\left(1 ; 1 ;-\frac{5}{3}\right)$ est normal au plan (IJG).
- Déterminer une équation du plan (IJG).
- Déterminer les coordonnées du point N , intersection du plan (IJG) et de la droite (BF).
- On admettra qu'un plan coupe 2 plans parallèles selon 2 droites parallèles. Tracer, sans justifier, la section du pavé ABCDEFGH par le plan (IJG).
Corrigé
-
- Les droites (IJ) et (BC) appartiennent au plan (AIJ), qui contient la face inférieure du pavé.
- Les droites (IJ) et (BC) sont sécantes en un point M.
Donc, comme (IJ) est dans le plan (IJG), le point M est aussi dans le plan (IJG). Et de même, comme (BC) est dans le plan (BCG), le point M est aussi dans le plan (BCG).
Par ailleurs, le point G est évidemment dans les plans (IJG) et (BCG).
Nous avons donc trouvé 2 points, M et G , qui appartiennent à la fois à (IJG) et à (BCG).
Donc les plans (IJG) et (BCG) se coupent selon la droite (MG).
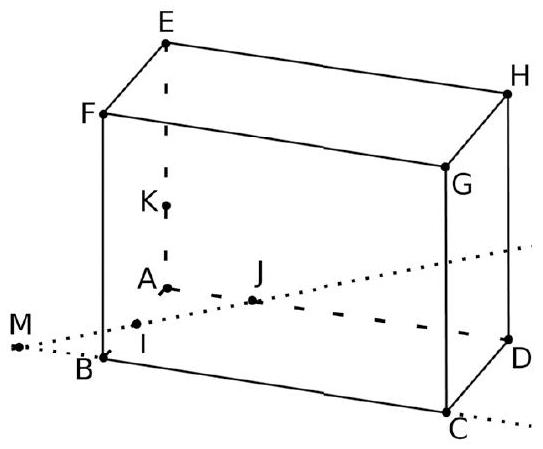
- La construction est ci-dessous.
Explication non demandée : Le point $N$ est sur $(B F)$, et donc dans le plan $(B C G)$. Or il est aussi dans (IJG). Donc il est dans l'intersection de (IJG) et (BCG), c'est-à-dire sur (MG). Finalement, il est à l'intersection des droites (MG) et (BF).
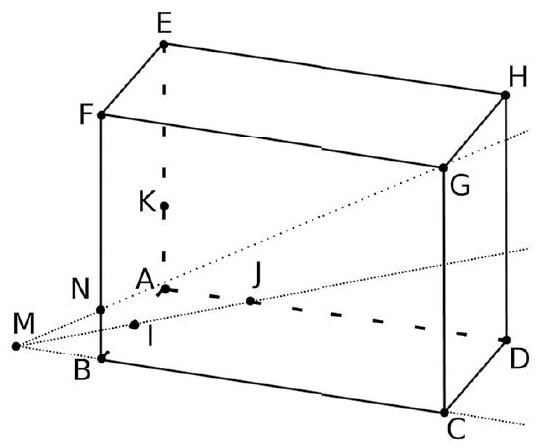
Remarque : nous pouvons calculer rapidement la distance BN en utilisant 2 fois le théorème de Thalès. $\left{\begin{aligned}(A J) / /(B M) & \ I & \in[A B] \ I & \in[J M]\end{aligned} \quad\right.$ donc $: \frac{M B}{J A}=\frac{B I}{A I} \quad$ soit : $\frac{M B}{1}=\frac{1}{1} \quad$ et donc : $M B=1$.
$$ \left{\begin{array}{l} (B N) / /(C G) \ B \in[M C] \quad \text { donc }: \frac{N B}{G C}=\frac{B M}{C M} \quad \text { soit }: \frac{N B}{3}=\frac{1}{5} \quad \text { et donc }: N B=\frac{3}{5} . \end{array}\right. $$
Nous retrouverons péniblement cette valeur dans la question 2. 2. L'espace est muni d'un repère orthonormal, ce qui autorise tous calculs de distances, normes ou produits scalaires.
- On obtient facilement : $\overrightarrow{I J}(-1 ; 1 ; 0)$.
On calcule alors : $\overrightarrow{I J} \cdot \vec{n}=(-1) \times 1+1 \times 1+0 \times=0$. De même, on obtient facilement: $\overrightarrow{I G}(1 ; 4 ; 3)$. On calcule alors : $\overrightarrow{I G} \cdot \vec{n}=1 \times 1+4 \times 1+3 \times\left(-\frac{5}{3}=0\right.$. Or le plan (IJG) admet pour vecteurs directeurs $\overrightarrow{I J}$ et $\overrightarrow{I G}$. Donc le vecteur $\vec{n}$ est normal au plan (IJG).
- Comme $\vec{n}\left(1 ; 1 ;-\frac{5}{3}\right)$ est normal à (IJG), ce dernier admet une équation du type : $x+y-\frac{5}{3} z+d=0$. Or, commme I ( $1 ; 0 ; 0$ ) est dans (IJG), ses coordonnées vérifient cette équation. Donc : $1+0-\frac{5}{3} \times 0+d=0$, et par là : $d=-1$. Donc (IJG) a pour équation cartésienne : $x+y-\frac{5}{3} z-1=0$.
- On obtient facilement: $\overrightarrow{B F}(0 ; 0 ; 3)$.
Or B a pour coordonnées ( $2 ; 0 ; 0$ ). Donc la droite $(\mathrm{BF})$ admet pour représentation paramétrique $\left{\begin{array}{l}x=2 \ y=0 \ z=3 t\end{array}\right.$ Le point N , intersection du plan (IJG) et de la droite (BF), voit ses coordonnées ( $x$; $y ; z)$ satisfaire à l'équation cartésienne du plan et à la représentation paramétrique : Donc : $\left{\begin{array}{l}x=2 \ y=0 \ z=3 t\end{array} \quad\right.$ et $\quad x+y-\frac{5}{3} z-1=0$. D'où : $2+0-\frac{5}{3} \times 3 t-1=0$. Et par là : $t=\frac{1}{5}$. On obtient donc finalement : $\left{\begin{array}{l}x=2 \ y=0 \ z=\frac{3}{5}\end{array}\right.$.
Donc N a pour coordonnées ( $2 ; 0 ; \frac{3}{5}$ ). Nous retrouvons la valeur remarquée dans la question 1. 3. La section est INGPJ.
Vous noterez que (PJ) et (GN) sont parallèles, car le plan (IJG) coupe 2 faces parallèles selon 2 droites parallèles.
Pour une raison analogue, (IN) est parallèle à (PG).
Exercice 6
L'espace est muni du repère orthonormal ( $\mathrm{O}, \mathrm{I}, \mathrm{J}, \mathrm{K}$ ). A a pour coordonnées ( $0 ; 1 ; 2$ ), B a pour coordonnées ( $1 ; 0 ; 5$ ), C a pour coordonnées ( $2 ;-1 ; 0$ ), D a pour coordonnées ( $-3 ; 0 ; 0$ ), E a pour coordonnées $(-0,5 ;-0,5 ; 4)$ et H a pour coordonnées $(2 ; 1 ; 1)$.
- Les points $\mathrm{A}, \mathrm{B}$ et C sont-ils alignés ?
- Le vecteur $\vec{n}(1 ; 1 ; 0)$ est-il un vecteur normal au plan (ABC) ?
- La droite ( DE ) et le plan ( ABC ) sont-ils sécants en un point F tel que E soit le milieu du segment [DF] ?
- Les droites $(\mathrm{AB})$ et $(\mathrm{CH})$ sont-elles sécantes ?
Corrigé
- On obtient facilement: $\overrightarrow{A B}(1 ;-1 ; 3)$.
La droite $(\mathrm{AB})$ passe par $\mathrm{A}(0,1,2)$ et a pour vecteur directeur $\overrightarrow{A B}(1 ;-1 ; 3)$.
Donc (AB) admet pour représentation paramétrique $\left{\begin{array}{c}x=0+t \ y=1-t \ z=2+3 t\end{array}\right.$ Or, si $\mathrm{C}(2,-1,0)$ appartenait à la droite $(\mathrm{AB})$, il existerait un réel $t$ tel que $\left{\begin{array}{c}2=0+t \ -1=1-t \ 0=2+3 t\end{array}\right.$ $\Leftrightarrow\left{\begin{aligned} t=2 \ -1=1-2 \ 0=2+3 \times 2\end{aligned} \Leftrightarrow\left{\begin{aligned} t & =2 \ -1 & =-1 \ 0 & =8\end{aligned}\right.\right.$ La dernière ligne est absurde. Donc C n'est pas sur la droite ( AB ). Donc les points $A, B$ et $C$ ne sont pas alignés. $C$ 'est pourquoi nous pouvons parler du plan (ABC) dans les questions qui suivent...
Autre méthode :
$\mathrm{A}, \mathrm{B}$ et C sont alignés si et seulement si les vecteurs $\overrightarrow{A B}$ et $\overrightarrow{A C}$ sont colinéaires. On obtient facilement : $\overrightarrow{A B}(1 ;-1 ; 3)$ et $\overrightarrow{A C}(2 ;-2 ;-2)$. Le vecteur $\overrightarrow{A B}$ n'étant pas nul, $\overrightarrow{A B}$ et $\overrightarrow{A C}$ sont colinéaires si et seulement si il existe un réel $k$ tel que $\overrightarrow{A C}=k \cdot \overrightarrow{A B}$. Soit : $\left{\begin{array}{c}2=k \times 1 \ -2=k \times(-1) \ -2=k \times 3\end{array}\right.$ Soit : $\left{\begin{array}{c}2=k \ 2=k \ \frac{-2}{3}=k\end{array}\right.$ Or les 2 dernières lignes sont contradictoires. Donc les vecteurs $\overrightarrow{A B}$ et $\overrightarrow{A C}$ ne sont pas colinéaires. Donc les points $\mathrm{A}, \mathrm{B}$ et C ne sont pas alignés. 2. Notons que le repère est orthonormé, ce qui nous autorise à calculer des produits scalaires. Les vecteurs $\overrightarrow{A B}(1 ;-1 ; 3)$ et $\overrightarrow{A C}(2 ;-2 ;-2)$ sont 2 vecteurs directeurs du plan (ABC). Or : $\overrightarrow{A B} \cdot \vec{n}=1 \times 1+(-1) \times 1+3 \times 0=0$.
Et : $\overrightarrow{A C} \cdot \vec{n}=2 \times 1+(-2) \times 1+(-2) \times 0=0$. Donc le vecteur $\vec{n}$ est un vecteur normal au plan (ABC). 3. Comme (ABC) admet $\vec{n}(1,1,0)$ pour vecteur normal, on en déduit que (ABC) admet une équation cartésienne du type : $1 x+1 y+0 z+d=0$, soit : $x+y+d=0$. Or le point $A(0,1,2)$ appartient à ( ABC ). Donc : $0+1+d=0$, et par là : $d=-1$. Donc $(\mathrm{ABC})$ a pour équation cartésienne : $x+y-1=0$ (1). Par ailleurs, on obtient facilement: $\overrightarrow{D E}(2,5 ;-0,5 ; 4)$. La droite (DE) passe par $\mathrm{D}(-3,0,0)$ et a pour vecteur directeur $\overrightarrow{D E}(2,5 ;-0,5$; $4)$. Donc (DE) admet pour représentation paramétrique : $\left{\begin{array}{c}x=-3+2.5 t \ y=0-0.5 t \ z=0+4 t\end{array}\right.$ Soit $F(x, y, z)$ le point d'intersection de (DE) et (ABC) (s'il existe). F étant sur (DE), il existe donc un réel $t$ tel que $\left{\begin{array}{c}x=-3+2.5 t \ y=0-0.5 t \ z=0+4 t\end{array}\right.$ Et comme F appartient à ( ABC ), on obtient, en reportant dans (1) : $-3+2,5 t-0,5 t-1=0$. Et par là : $t=2$. Le réel $t$ existe et est unique, ce qui prouve que ( DE ) et ( ABC ) sont bien sécants. Leur point d'intersection F a pour coordonnées : $\left{\begin{array}{c}x=-3+2.5 \times 2 \ y=0-0.5 \times 2 \ z=0+4 \times 2\end{array}\right.$ On a donc $F(2 ;-1 ; 8)$. Il reste à vérifier si E est le milieu du segment $[\mathrm{DF}]$. On a: $\frac{x_{D}+x_{F}}{2}=\frac{-3+2}{2}=-0,5=x_{E}$. Et : $\frac{y_{D}+y_{F}}{2}=\frac{0+(-1)}{2}=-0,5=y_{E}$. Et : $\frac{z_{D}+z_{F}}{2}=\frac{0+8}{2}=4=z_{E}$. Donc E est effectivement le milieu du segment $[\mathrm{BF}]$. 4. Pour que les droites ( AB ) et ( CH ) soient sécantes, il est nécessaire qu'elles soient coplanaires. Montrons que ce n'est pas le cas. $\mathrm{Si}(\mathrm{AB})$ et $(\mathrm{CH})$ étaient coplanaires, alors le point H appartiendrait au plan (ABC).
Or: $x_{H}+y_{H}-1=2+1-1=2$. Et donc : $x_{H}+y_{H}-1=2+1-1 \neq 0$. Les coordonnées de H ne vérifient donc pas l'équation cartésienne de ( ABC ). Donc H n'est pas dans ( ABC ). Et donc ( $\mathbf{A B}$ ) et ( $\mathbf{C H}$ ) ne sont pas sécantes.
Autre méthode (utile si on ne dispose pas de l'équation cartésienne de (ABC)). On obtient facilement une représentation paramétrique de $(\mathrm{CH}):\left{\begin{array}{c}x=2+0 t^{\prime} \ y=-1+2 t^{\prime} \ z=0+1 t^{\prime}\end{array}\right.$ Or (AB) admet pour représentation paramétrique $\left{\begin{array}{l}x=0+t \ y=1-t \ z=2+3 t\end{array}\right.$ Les coordonnées du point d'intersection des 2 droites vérifient les 2 représentations. D'où : $\left{\begin{array}{c}2+0 t^{\prime}=0+t \ -1+2 t^{\prime}=1-t \ 0+1 t^{\prime}=2+3 t\end{array}\right.$ Soit : $\left{\begin{array}{c}2=t \ -1+2 t^{\prime}=1-2 \ 1 t^{\prime}=2+3 \times 2\end{array}\right.$ Soit : $\left{\begin{array}{l}2=t \ t^{\prime}=0 \ t^{\prime}=8\end{array}\right.$ Les 2 dernières lignes étant contradictoires, le point d'intersection des 2 droites n'existe pas. Et par là, les droites ne sont pas sécantes.
Exercice 7
Un architecte veut réaliser un toit incliné triangulaire selon le modèle ci-dessous.
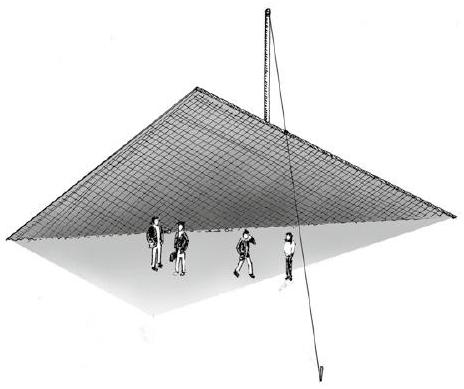
Un mat situé derrière le toit retient ce dernier par l'intermédiaire d'un cable d'acier tendu entre le sommet de ce mat et le sol.
L'architecte simplifie le dessin selon la figure suivante. Le toit est le triangle ABC .
Le segment $[\mathrm{AB}]$ est au sol. Le point C est le sommet du toit. Un filin métallique (non représenté pour l'instant) sera tendu entre le sommet $S$ du mât $[\mathrm{OS}]$ et le sol (OAB). Le filin sera orthogonal au toit. Ce filin sera fixé au sol au point M , et au toit au point P .
Le but de l'exercice est de déterminer les positions exactes des points $M$ et $P$. L'espace est muni du repère orthonormal ( $\mathrm{O}, \mathrm{I}, \mathrm{J}, \mathrm{K}$ ). A a pour coordonnées $(0 ; 1 ; 0)$, B a pour coordonnées $(1 ;-1 ; 0)$, C a pour coordonnées $(1 ; 0 ; 1)$, S a pour coordonnées $(0 ; 0 ; 1)$,
- Les points $\mathrm{A}, \mathrm{B}$ et C sont-ils alignés ?
- Le vecteur $\vec{n}(-2 ;-1 ; 1)$ est-il un vecteur normal au plan (ABC) ?
- Déterminer une équation paramétrique de la droite $d$ passant par S et perpendiculaire au plan (ABC).
- Soit M le point d'intersection de la droite $d$ et du plan ( OAB ).
Déterminer les coordonnées du point M . 5. Déterminer une équation cartésienne du plan ( ABC ). 6. Soit P le point d'intersection de la droite $d$ et du plan ( ABC ).
Montrer que P est sur la droite (CA). 7. Calculer la distance CP. 8. Compléter le dessin proposé en plaçant précisément les points M et P .
Corrigé
- On obtient facilement : $\overrightarrow{A B}(1 ;-2 ; 0) \quad \overrightarrow{A C}(1 ;-1 ; 1)$. $\overrightarrow{A B}$ et $\overrightarrow{A C}$, vecteurs non nuls dont les coordonnées ne sont pas proportionnelles, ne sont donc pas colinéaires. Les points $\mathrm{A}, \mathrm{B}$ et C ne sont donc pas alignés. $C$ 'est pourquoi nous pouvons parler du plan (ABC) dans les questions qui suivent...
Notons de plus que les vecteurs $\overrightarrow{A B}$ et $\overrightarrow{A C}$ forment donc un couple de vecteurs directeurs du plan (ABC). 2. On a: $\overrightarrow{A B} \cdot \vec{n}=1 \times(-2)-2 \times(-1)+0 \times 1=0$. et : $\overrightarrow{A C} \cdot \vec{n}=1 \times(-2)-1 \times(-1)+1 \times 1=0$. Or $\overrightarrow{A B}$ et $\overrightarrow{A C}$ forment un couple de vecteurs directeurs du plan (ABC). Donc le vecteur $\vec{n}(-2 ;-1 ; 1)$ est effectivement un vecteur normal au plan (ABC). 3. La droite $d$ passe par $\mathrm{S}(0 ; 0 ; 1)$.
Or elle est perpendiculaire au plan (ABC) de vecteur normal $\vec{n}(-2 ;-1 ; 1)$. Donc $d$ admet pour représentation paramétrique $\left{\begin{array}{c}x=-2 t \ y=-t \ z=t+1\end{array}\right.$ 4. Le point $\mathrm{M}(x ; y ; z)$ appartient à la fois à la droite $d$ et au plan ( OAB ).
Il existe donc un réel $t$ tel que $\left{\begin{array}{c}x=-2 t \ y=-t \ z=t+1\end{array}\right.$. Et comme le plan $(\mathrm{OAB})$ a pour équation cartésienne : $z=0$ (évident), on obtient : $\left{\begin{array}{c}x=-2 t \ y=-t . \ 0=t+1 .\end{array}\right.$ Et par là : $\left{\begin{array}{c}x=2 \ y=1 \ t=-1\end{array}\right.$. Donc M ( $2 ; 1 ; 0$ ). 5. Déterminons une équation cartésienne du plan $(\mathrm{ABC})$. $\vec{n}(-2 ;-1 ; 1)$ est un vecteur normal de (ABC). Le plan $(\mathrm{ABC})$ admet donc pour une équation cartésienne du type : $-2 \times x-1 \times y+z+d=0$. Or A ( $0 ; 1 ; 0$ ) est dans P ; donc : $-2 \times 0-1 \times 1+0+d=0$, d'où : $d=1$. Donc $(\mathrm{ABC})$ admet pour équation cartésienne $-2 \times x-1 \times y+z+1=0$. 6. Déterminons les coordonnées de $\mathrm{P}(x ; y ; z)$.
P est le point d'intersection de la droite $d$ et du plan (ABC). Il existe donc un réel $t$ tel que $\left{\begin{array}{c}x=-2 t \ y=-t \ z=t+1\end{array}\right.$. Or le plan $(\mathrm{ABC})$ a pour équation cartésienne : $-2 \times x-1 \times y+z+1=0$. Donc on obtient: $-2 \times(-2 t)-1 \times(-t)+t+1+1=0$. Et donc : $t=\frac{-1}{3}$. Et par conséquent : $\left{\begin{array}{l}x=\frac{2}{3} \ y=\frac{1}{3} \ 0=\frac{2}{3}\end{array}\right.$. Donc $\mathrm{P}\left(\frac{2}{3} ; \frac{1}{3} ; \frac{2}{3}\right)$.
Montrons que P est sur la droite (CA). On obtient facilement : $\overrightarrow{C P}\left(-\frac{1}{3} ; \frac{1}{3} ;-\frac{1}{3}\right) \quad \overrightarrow{A C}(1 ;-1 ; 1)$. On constate alors que $: \overrightarrow{C P}=-\frac{1}{3} \overrightarrow{A C}$. $\overrightarrow{C P}$ et $\overrightarrow{A C}$ sont donc colinéaires. Donc les points $A, P$ et $C$ sont alignés. Et par là, P est sur la droite $(\mathrm{CA})$. 7. On calcule finalement: $\overrightarrow{C P} \cdot \overrightarrow{C P}=\left(-\frac{1}{3}\right)^{2}+\left(-\frac{1}{3}\right)^{2}+\left(-\frac{1}{3}\right)^{2}=\frac{1}{3}$. et par là : $C P=\sqrt{\frac{1}{3}}$. 8. Pour compléter la figure, on trace d'abord les axes du repère.
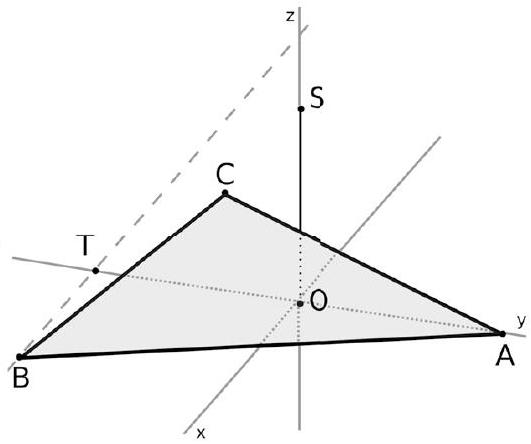
L'axe Oy passe par O et A (évident). L'axe Oz passe par O et S (évident). Pour déterminer l'axe Ox , on place d'abord le point $\mathrm{T}(0 ;-1 ; 0)$. Puis on trace la droite (TB). L'axe Ox passe par O et est parallèle à la droite $(\mathrm{TB})$. Une illusion d'optique laisse croire, à tort, que ces droites ne sont pas parallèles sur le dessin.
La figure est alors ci-contre.
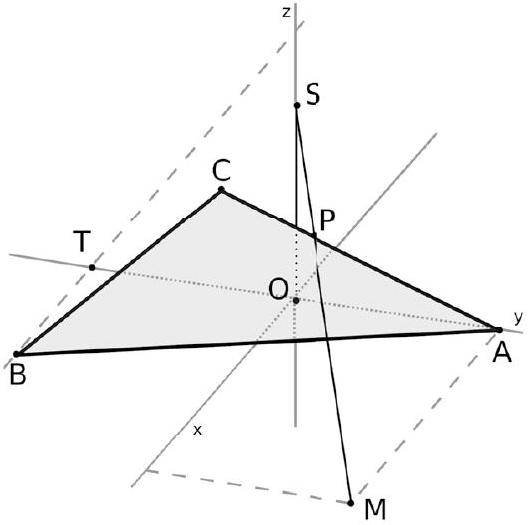
La figure terminée est finalement la suivante (on a placé M , puis P ).

Aucun commentaire à afficher
Aucun commentaire à afficher