Cours : Dérivation

Dérivation

Un conseil : revoir le cours sur la dérivation de la classe de première !

I Dérivées et sens de variation

a. Composées

Composée

Soit $u$ une fonction définie sur un ensemble A. Soit $v$ une fonction définie sur un ensemble B . On suppose de plus que, pour tout $x$ de $\mathrm{A}, u(x)$ appartient à B . La composée de $u$ par $v$, notée $v o u$ (on dit «v rond u »), est la fonction, définie sur l'ensemble A telle que : pour tout $x$ de A , $\square$ $\operatorname{vou}(x)=v(u(x))$

Retenir le schéma suivant :

$$ \mathrm{A} \xrightarrow{u} \mathrm{~B} \xrightarrow{v} \mathbf{R} $$

Retenir le schéma suivant :

$$ x \quad \longmapsto u(x) \longmapsto v \circ u(x)=v(u(x)) $$

Remarque

Par la suite, les ensembles A et B seront qualifiés de « convenables » lorsqu'ils assureront l'existence de la composée (ou de ses dérivées).

b. Calculs de dérivées

Propriété

Les tableaux suivants donnent les fonctions de référence, leurs dérivées, et les intervalles sur lesquels sont définies ces dérivées.

Fonctions et dérivées vues en terminale

Fonction	Dérivée	Intervalle
$f(x)=\ln x$	$f^{\prime}(x)=\frac{1}{x}$	$\mathbf{R}_{+}^{*}$
$f(x)=\cos x$	$f^{\prime}(x)=-\sin x$	$\mathbf{R}$
$f(x)=\sin x$	$f^{\prime}(x)=\cos x$	$\mathbf{R}$

Fonctions et dérivées vues en première

Fonction	Dérivée	Intervalle
$f(x)=k$	$f^{\prime}(x)=0$	R
$f(x)=x$	$f^{\prime}(x)=1$	R
$f(x)=a x+b$	$f^{\prime}(x)=a$	R
$f(x)=x^{2}$	$f^{\prime}(x)=2 x$	R
$f(x)=x^{3}$	$f^{\prime}(x)=3 x^{2}$	R
$f(x)=\frac{1}{x}$	$f^{\prime}(x)=-\frac{1}{x^{2}}$	$]-\infty ; 0[$ ou $] 0 ;+\infty[$
$f(x)=\sqrt{x}$	$f^{\prime}(x)=\frac{1}{2 \sqrt{x}}$	$] 0 ;+\infty[$
$f(x)=x^{n}$ avec $n \in \mathbf{Z}$ et $n \neq 0$	$f^{\prime}(x)=n x^{n-1}$	$\mathbf{R}$ si $n>0 \quad \mathbf{R}{-}^{*}$ our $\mathbf{R}{+}^{*}$ si $n<0$
$f(x)=e^{x}$	$f^{\prime}(x)=e^{x}$	R

Opérations

Le tableau ci-après donne les dérivées d'une somme, d'un produit et d'un quotient de fonctions $u$ et $v$ dérivables sur un même intervalle I (Pour la dérivée du quotient, $v$ est supposée ne pas s'annuler sur I).

Fonction	Dérivée
$u+v$	$u^{\prime}+v^{\prime}$
$u v$	$u^{\prime} v+u v^{\prime}$
$\frac{u}{v}$	$\frac{u^{\prime} v-u v^{\prime}}{v^{2}}$

Cas particuliers :

Si $k$ une constante, alors la dérivée de $k u$ est $k u^{\prime}$. La dérivée de $\frac{1}{v}$ est $\frac{-v^{\prime}}{v^{2}}$.

Propriété Dérivée d'une composée

Si $u$ et $v$ sont des fonctions dérivables sur des intervalles convenables, alors la dérivée de la fonction vou est la fonction $u^{\prime} \times\left(v^{\prime} \circ u\right)$

Cas particuliers

Soit $u$ est une fonction dérivable sur un intervalle convenable.

La dérivée de la fonction $e^{u}$ est la fonction $u^{\prime} e^{u}$.

La dérivée de la fonction $\sqrt{u}$ est la fonction $\frac{u^{\prime}}{2 \sqrt{u}}$.

La dérivée de la fonction $u^{n}$ (pour $n$ entier relatif non nul) est la fonction $n u^{\prime} u^{n-1}$.

La dérivée de la fonction $u(a x+b)$ (pour a et $b$ réels) est la fonction $a u^{\prime}(a x+b)$. La dérivée de la fonction $\ln u$ est la fonction $\frac{u^{\prime}}{u}$ (cette dernière fonction est vue en terminale).

c. Sens de variation

Propriété

Soit I un intervalle. $f^{\prime}=0$ sur I si et seulement si $f$ est constante sur I. $f^{\prime} \geq 0$ sur I si et seulement si $f$ est croissante sur I. $f^{\prime}>0$ presque partout sur I si et seulement si $f$ est strictement croissante sur I. $f^{\prime} \leq 0$ sur I si et seulement si $f$ est décroissante sur I. $f^{\prime}<0$ presque partout sur I si et seulement si $f$ est strictement décroissante sur I.

Savoir faire

À quoi peut servir la dérivée d'une fonction? La valeur de la dérivée en un point permet d'y déterminer le coefficient directeur de la tangente à la courbe de la fonction en ce point. Le signe de la dérivé permet de déterminer le sens de variation de la fonction. Dériver une fonction permet de vérifier qu'elle est bien une primitive d'une autre fonction (voir chapitre sur les primitives).

II Convexité

Définition

Une fonction dérivable sur un intervalle I est convexe si et seulement si sa courbe est entièrement située au-dessusde chacune de ses tangentes. Une fonction dérivable sur un intervalle I est concave si et seulement si sa courbe est entièrement située en dessous de chacune de ses tangentes.

Propriété

Fonctions vues en première

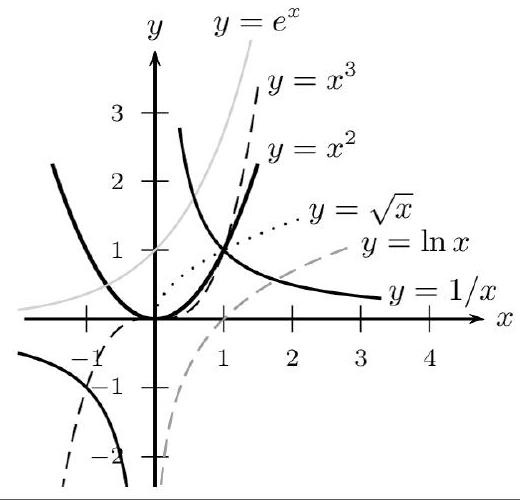
La fonction $x^{2}$ est convexe sur $\mathbb{R}$. La fonction $x^{3}$ est convexe sur $[0 ;+\infty[$, mais elle est concave sur $]-\infty ; 0]$. La fonction $\frac{1}{x}$ est convexe sur $] 0 ;+\infty[$, mais elle est concave sur $]-\infty ; 0[$. La fonction $\sqrt{x}$ est concave sur $[0 ;+\infty[$. La fonction $e^{x}$ est convexe sur $\mathbb{R}$.

Fonction vue en terminale

La fonction $\ln x$ est concave sur $] 0 ;+\infty[$.

Propriété

Soit I un intervalle. $f$ est convexe sur I si et seulement si $-f$ est concave sur I.

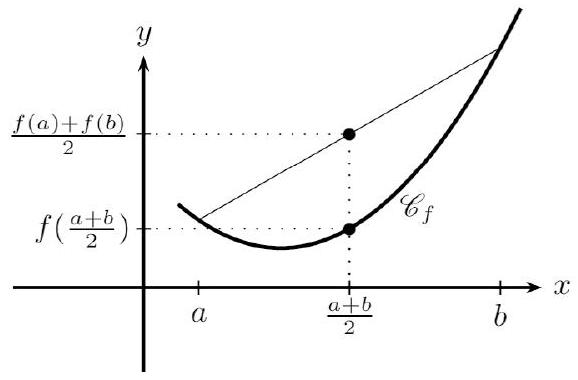
Milieu d'une corde

Soit $f$ une fonction continue sur un intervalle I. $f$ est convexe sur I si et seulement si, pour tous $a$ et $b$ de I, $f\left(\frac{a+b}{2}\right) \leq \frac{f(a)+f(b)}{2}$.

Propriété

Soit $f$ une fonction dérivable sur un intervalle I. $f$ est convexe sur I si et seulement si $f^{\prime}$ est croissante sur I. $f$ est concave sur I si et seulement si $f^{\prime}$ est décroissante sur I.

Propriété

Soit $f$ une fonction dérivable deux fois sur un intervalle $] a ; b[$. Si $f^{\prime \prime} \geq 0$ sur $] a ; b[$, alors $f$ est convexe sur sur $] a ; b[$. Si $f^{\prime \prime} \leq 0$ sur $] a ; b[$, alors $f$ est concave sur sur $] a ; b[$. Cette propriété est valable si $a=-\infty$ ou $b=+\infty$.

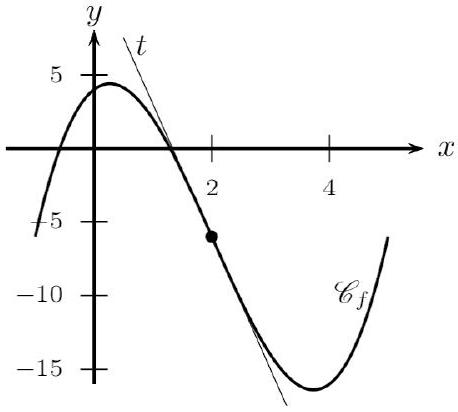
Définition

Le point A est un point d'inflexion de la courbe $\mathrm{C}{f}$ lorsque la courbe $\mathrm{C}{f}$ y traverse sa tangente $t$.

Propriété

Soit $f$ une fonction dérivable deux fois sur un intervalle $] a ; b[$. Si $f^{\prime \prime}$ s'annule en $c$ en changeant de signe, alors le point $A(c ; f(c))$ est un point d'inflexion de $\mathrm{C}_{f}$.

À quoi peut servir la convexité d'une fonction $f$ ? La convexité permet de déterminer la position de $\mathrm{C}{f}$ par rapport à ses tangentes. Le changement de convexité permet de repérer les points d'inflexion de $\mathrm{C}{f}$.