Exercices corrigés

Exercices corrigés

Exercice 1

On pose : $u(x)=\frac{1}{x}+3$, définie sur $] 0 ;+\infty[$. On pose: $v(x)=(x-2)^{2}+5$, définie sur $\mathbb{R}$.

1. Montrer que la composée vou existe et est définie sur $] 0 ;+\infty[$.
2. Déterminer l'expression de $\operatorname{vou}(x)$ pour tout $x$ de $] 0 ;+\infty[$.
3. Montrer que la composée uov existe et est définie sur $\mathbb{R}$.
4. Déterminer l'expression de $\operatorname{uov}(x)$ pour tout $x$ de $\mathbb{R}$.

Corrigé

1. L'existence de vou ne pose pas de problème car, pour tout $x$ de $] 0 ;+\infty[, u(x)$ appartient évidemment à $\mathbb{R}$.
2. $\operatorname{vou}(x)=v(u(x))=(u(x)-2)^{2}+5=\left(\frac{1}{x}+3-2\right)^{2}+5=\left(\frac{1}{x}+1\right)^{2}+5$.
3. On note que, pour tout $x$ de $\mathbb{R}, v(x)$ appartient à $] 0 ;+\infty[$ (car le minimum de $v$ est clairement 5). Donc uov existe. Elle est définie sur $\mathbb{R}$.
4. $u o v(x)=u(v(x))=\frac{1}{v(x)}+3=\frac{1}{(x-2)^{2}+5}+3$.

Exercice 2

Cet exercice utilise exclusivement des fonctions vues en première. Déterminer $f^{\prime}$, puis le signe de $f^{\prime}$ sur I , et dresser alors le tableau de variation de $f$ sur l'intervalle I (sans les limites) dans chacun des cas suivants :

1. $f(x)=\sqrt{x}+x^{3}+x$ sur $\left.I=\right] 0 ;+\infty[$
2. $f(x)=-5 x^{2}+x+3$ sur $I=\mathbb{R}$
3. $f(x)=8 x^{2}-x+9$ sur $I=\left[0 ; \frac{1}{16}\right]$
4. $f(x)=-x^{3}+\frac{3}{2} x^{2}$ sur $I=\mathbb{R}$
5. $f(x)=-2 x^{3}-0,5 x^{2}+x+3$ sur $\mathbb{R}$
6. $f(x)=\frac{x^{2}}{2 x+1}$ sur $I=[-1 ;-0,5[$

Corrigé

1. $f(x)=\sqrt{x}+x^{3}+x$ sur $\left.I=\right] 0 ;+\infty[$. $f^{\prime}(x)=\frac{1}{2 \sqrt{x}}+3 x^{2}+1$. $f^{\prime}$ est une somme de termes. Les termes $\frac{1}{2 \sqrt{x}}$ et $3 x^{2}$ sont positifs, le terme 1 est strictement positif. Donc $f^{\prime}$ est strictement positive sur $\left.I=\right] 0 ;+\infty[$. D'où le tableau de variation de $f$ sur I.

$x$	0	$+\infty$
$f^{\prime}(x)$	+
$f(x)$

2. $f(x)=-5 x^{2}+x+3$ sur $I=\mathbb{R}$. Donc $f^{\prime}(x)=-5 \times 2 x+1+0=-10 x+1$. $f^{\prime}$ est une fonction affine de coefficient -10 strictement négatif. On note que : $-10 x+1=0 \Leftrightarrow-10 x=-1 \Leftrightarrow x=\frac{-1}{-10}=0,1$. D'où le tableau de variation de $f$ sur I.

$x$	$-\infty$	0,1		$+\infty$
$f^{\prime}(x)$		+	0	-
$f(x)$

3. $f(x)=8 x^{2}-x+9 \operatorname{sur} I=\left[0 ; \frac{1}{16}\right]$. $f^{\prime}(x)=8 \times 2 x-1+0=16 x-1$. $f^{\prime}$ est une fonction affine de coefficient 16 strictement positif. On note que : $16 x-1=0 \Leftrightarrow 16 x=1 \Leftrightarrow x=\frac{1}{16}$. D'où le tableau de variation de $f$ sur I.

$x$	0		$1 / 16$
$f^{\prime}(x)$		-	0
	9
$f(x)$
			8,96875

4. $f(x)=-x^{3}+\frac{3}{2} x^{2}$ sur $I=\mathbb{R}$. $f^{\prime}(x)=-3 x^{2}+\frac{3}{2} 2 x=-3 x^{2}+3 x=-3 x(x-1)$. $f^{\prime}$ est un produit de 2 facteurs, chacun d'eux étant une fonction affine (voire linéaire pour le premier). $-3 x$ a pour coefficient -3 strictement négatif. $x-1$ a pour coefficient 1 strictement positif. On note que : $-3 x=0 \Leftrightarrow x=\frac{0}{-3}=0$. On note que : $x-1=0 \Leftrightarrow x=1$. D'où le tableau de variation de $f$ sur I.

$x$	$-\infty$		0		1		$+\infty$
$-3 x$		+	0	-	$\mid$	-
$x-1$		-	$\mid$	-	0	+
$f^{\prime}(x)$		-	0	+	0	-
					0,5
$f(x)$

5. $f(x)=-2 x^{3}-0,5 x^{2}+x+3$ sur $\mathbb{R}$. $f^{\prime}(x)=-2 \times 3 x^{2}-0,5 \times 2 x+1=-6 x^{2}-x+1$. $f^{\prime}$ est un trinôme avec $a=-6, b=-1$ et $c=1$. $\Delta=b^{2}-4 a c=(-1)^{2}-4 \times(-6) \times 1=25$. $\Delta>0$. Le trinôme a 2 racines $x_{1}=\frac{-b-\sqrt{\Delta}}{2 a}=\frac{1-5}{-12}=\frac{1}{3} \quad$ et $x_{2}=\frac{-b+\sqrt{\Delta}}{2 a}=\frac{1+5}{-12}=-0,5$. $a<0$. D'où le tableau suivant :

$x$	$-\infty$	-0.5	$\frac{1}{3}$	$+\infty$
-6	-	$\mid$	-	$\mid$	-
$x-\frac{1}{3}$	-	$\mid$	-	0	+
$x+0,5$	-	0	+	$\mid$	+
$f^{\prime}(x)$	-	0	+	$\emptyset$	-
				$f(1 / 3) \approx 3,204$
$f(x)$

6. $f(x)=\frac{x^{2}}{2 x+1}$ sur $I=[-1 ;-0,5[$.

On pose $f=\frac{u}{v}$ avec $u=x^{2}$ et $v=2 x+1$. D'où $f^{\prime}=\frac{u^{\prime} v-u v^{\prime}}{v^{2}}$ avec $u^{\prime}=2 x$ et $v^{\prime}=2$. Soit $f^{\prime}(x)=\frac{2 x \times(2 x+1)-x^{2} \times 2}{(2 x+1)^{2}}=\frac{4 x^{2}+2 x-2 x^{2}}{(2 x+1)^{2}}=\frac{2 x^{2}+2 x}{(2 x+1)^{2}}=\frac{2 x(x+1)}{(2 x+1)^{2}}$.

Le numérateur est un produit de 2 facteurs, chacun d'eux étant une fonction affine (voire linéaire pour le premier). $2 x$ a pour coefficient 2 strictement positif. $x+1$ a pour coefficient 1 strictement positif. On note que : $2 x=0 \Leftrightarrow x=\frac{0}{2}=0$. On note que : $x+1=0 \Leftrightarrow x=-1$. Le dénominateur est un carré strictement positif pour $x \neq-0,5$. D'où le tableau de variation de $f$ sur I.

$x$	-1		$-0,5$
$2 x$		-
$x+1$	0	+
$(2 x+1)^{2}$		+	0
$f^{\prime}(x)$		-
	-1
$f(x)$

Exercice 3

Cet exercice utilise parfois des fonctions vues en terminale. Les questions 3. et 4. utilisent la fonction logarithme népérien Déterminer $f^{\prime}$, puis le signe de $f^{\prime}$ sur I , et dresser alors le tableau de variation de $f$ sur l'intervalle I (sans les limites) dans chacun des cas suivants :

1. $f(x)=5 e^{-x^{2}+1} \operatorname{sur} I=\mathbb{R}$
2. $f(x)=e^{5 x+1}+6 x \operatorname{sur} I=\mathbb{R}$
3. $f(x)=e^{5 x+1}-6 x$ sur $I=\mathbb{R}$
4. $f(x)=5 x \ln x+x \operatorname{sur} I=] 0 ;+\infty[$

Corrigé

1. $f(x)=5 e^{-x^{2}+1}$ sur $I=\mathbb{R}$.

On pose $f=k e^{u}$ avec $k=5$ et $u=-x^{2}+1$. D'où $f^{\prime}=k u^{\prime} e^{u}$ avec $u^{\prime}=-2 x$. Soit $f^{\prime}(x)=5 \times(-2 x) \times e^{-x^{2}+1}=-10 x e^{-x^{2}+1}$. $f^{\prime}$ est un produit de 2 facteurs. $-10 x$ est linéaire, de coefficient -10 strictement négatif, et s'annule pour $x=0$. $e^{-x^{2}+1}$ est une exponentielle, et donc strictement positive.

D'où le tableau de variation de $f$ sur I.

$x$	$-\infty$		0		$+\infty$
$-10 x$		+	$\emptyset$	-
$e^{-x^{2}+1}$		+		+
$f^{\prime}(x)$		+	$\emptyset$	-
			$5 e$
$f(x)$

2. $f(x)=e^{5 x+1}+6 x \operatorname{sur} I=\mathbb{R}$.

On pose $f=e^{u}+6 x$ avec $u=5 x+1$. D'où $f^{\prime}=u^{\prime} e^{u}+6 \operatorname{avec} u^{\prime}=5$. Soit $f^{\prime}(x)=5 e^{5 x+1}+6$. $f^{\prime}$ est une somme de termes. L'exponentielle $e^{5 x+1}$ est strictement positive et 5 également. Donc le premier terme $5 e^{5 x+1}$ est strictement positif. Or le second terme 6 est strictement positif. Donc $f^{\prime}$ est strictement positive. D'où le tableau de variation de $f$ sur I.

$x$	$-\infty$	$+\infty$
$f^{\prime}(x)$	+
$f(x)$

3. $f(x)=e^{5 x+1}-6 x$ sur $I=\mathbb{R}$.

On pose $f=e^{u}-6 x$ avec $u=5 x+1$. D'où $f^{\prime}=u^{\prime} e^{u}-6$ avec $u^{\prime}=5$. Soit $f^{\prime}(x)=5 e^{5 x+1}-6$. $f^{\prime}$ est une somme de termes. Mais $5 e^{5 x+1}>0$ alors que $-6<0$. On va chercher pour quels $x$ l'expression $5 e^{5 x+1}-6$ est positive. Par conséquent, on résout $5 e^{5 x+1}-6>0$. Soit $5 e^{5 x+1}-6>0 \Leftrightarrow 5 e^{5 x+1}>6 \Leftrightarrow e^{5 x+1}>\frac{6}{5}$. Soit $5 e^{5 x+1}-6>0 \Leftrightarrow \ln \left(e^{5 x+1}\right)>\ln \left(\frac{6}{5}\right) \Leftrightarrow 5 x+1>\ln (1,2)$. Soit $5 e^{5 x+1}-6>0 \Leftrightarrow 5 x>\ln (1,2)-1 \Leftrightarrow x>\frac{\ln (1,2)-1}{5}$. De même, on obtient $5 e^{5 x+1}-6=0 \Leftrightarrow x=\frac{\ln (1,2)-1}{5}$

D'où le tableau de variation de $f$ sur I.

$x$	$-\infty$		$\frac{\ln 1,2-1}{5}$	$+\infty$
$f^{\prime}(x)$	-	0	+
$f(x)$
			$f\left(\frac{\ln 1,2-1}{5}\right)$

4. $f(x)=5 x \ln x+x \operatorname{sur} I=] 0 ;+\infty[$.

On pose $f=u v+x$ avec $u=5 x$ et $v=\ln x$. D'où $f^{\prime}=u^{\prime} v+u v^{\prime}+1$ avec $u^{\prime}=5$ et $v^{\prime}=\frac{1}{x}$. Soit $f^{\prime}(x)=5 \ln \mathrm{x}+5 x \frac{1}{x}+1=5 \ln x+5+1=5 \ln x+6$. $f^{\prime}$ est une somme de termes. $6>0$, mais le signe de $5 \ln x$ est variable. On va chercher pour quels $x$ l'expression $5 \ln x+6$ est positive. Par conséquent, on résout $5 \ln x+6>0$. $5 \ln x+6>0 \Leftrightarrow \ln x>\frac{-6}{5} \Leftrightarrow e^{\ln x}>e^{\frac{-6}{5}} \Leftrightarrow x>e^{-1,2}$. De même, on obtient $5 \ln x+6=0 \Leftrightarrow x=e^{-1,2}$. D'où le tableau de variation de $f$ sur I.

$x$	0		$e^{-1,2}$	$+\infty$
$f^{\prime}(x)$	-	0	+
$f(x)$

Exercice 4

Cet exercice utilise des fonctions vues en terminale, en particulier la question 3., qui utilise la fonction logarithme népérien. Déterminer la dérivée de la fonction, puis le signe de sa dérivée, puis le sens de variation de la fonction sur l'intervalle I dans chacun des cas suivants :

1. $n(x)=2 \sqrt{x^{2}+1}+(3 x+1)^{2}$ avec $\left.I=\right] 0$; 2]
2. $o(x)=(\sin x)^{2}$ avec $\left.I=\right] \frac{\pi}{2} ; \pi[$
3. $p(x)=\ln (-3 x+5)$ avec $I=\left[0 ; \frac{5}{3}[\right.$

Corrigé

1. Dérivons $n(x)=2 \sqrt{x^{2}+1}+(3 x+1)^{2}$.

On pose $u=x^{2}+1$. Donc $u^{\prime}=2 x$. De même $w=3 x+1$. Donc $w^{\prime}=3$. Ici $n=2 \sqrt{u}+w^{2}$ et donc $n^{\prime}=2 \frac{u^{\prime}}{2 \sqrt{u}}+2 w^{\prime} w$. Donc $n^{\prime}(x)=2 \times \frac{2 x}{2 \sqrt{x^{2}+1}}+2 \times 3 \times(3 x+1)=\frac{2 x}{\sqrt{x^{2}+1}}+18 x+6$. Malheureusement, $n$ ' $(x)$ est une somme. Or le signe d'une somme n'est évident que si tous les termes sont de même signe. Mais nous allons montrer qu'ici, c'est le cas $!$ $\sqrt{x^{2}+1}$ est strictement positif pour tout $x$. Or, sur $I: 2 x>0$. Donc, sur $I$, le quotient $\frac{2 x}{\sqrt{x^{2}+1}}$ est strictement positif. Par ailleurs, sur $I: 18 x+6>0$. Donc les deux termes constituant $n^{\prime}(x)$ sont strictement positifs sur $I$. Et finalement, sur $I, n^{\prime}(x)>0$. Donc $n$ est strictement croissante sur I. 2. Dérivons $o(x)=(\sin x)^{2}$.

On pose $u=\sin x$. Donc $u^{\prime}=\cos x$. ici $o=u^{2}$. Donc $o^{\prime}=2 u^{\prime} u$. Donc $o^{\prime}(x)=2 \times \cos x \times \sin x$. $o^{\prime}(x)$ est un produit de 3 facteurs dont nous allons trouver les signes. On a : $2>0$. Sur $I: \cos x<0$. Sur $I: \sin x>0$. Finalement, sur $I, o^{\prime}(x)<0$. Donc $o$ est strictement décroissante sur I. 3. Dérivons $p(x)=\ln (-3 x+5)$.

On pose $u(x)=-3 x+5$. Donc $u^{\prime}(x)=-3$. ici $p(x)=\ln u$. Donc $p^{\prime}(x)=\frac{u^{\prime}}{u}$. Donc $p^{\prime}(x)=\frac{-3}{-3 x+5}$. $p^{\prime}(x)$ est un quotient dont nous allons trouver les signes du dénominateur et du numérateur. La fonction affine $-3 x+5$ s'annule en $\frac{5}{3}$, et est strictement positive pour $x<\frac{5}{3}$. Donc, sur I: $-3 x+5>0$. Or $p^{\prime}$ a pour numérateur -3 qui est strictement négatif. Finalement, sur $I, p^{\prime}(x)<0$. Donc $p$ est strictement décroissante sur I.

Exercice 5

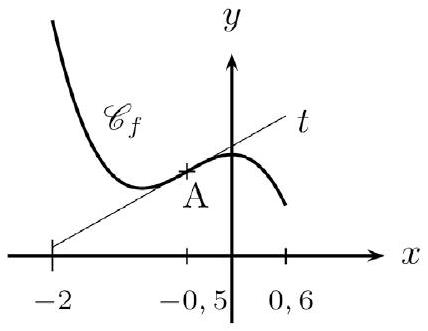
La tangente $t$ à $\mathrm{C}{f}$ en $-0,5$ traverse $\mathrm{C}{f}$. Déterminer graphiquement la convexité de la fonction $f$ définie sur $[-2 ; 0,6]$. En déduire le sens de variation de $f^{\prime}$ et le signe de $f^{\prime \prime}$ sur $[-2 ; 0,6]$.

Corrigé

Il est évident que $f$ est convexe sur $[-2 ;-0,5]$ (car $\mathrm{C}{f}$ y est au-dessus de ses tangentes), et concave sur $[-0,5 ; 0,6]$ ( $\operatorname{car} \mathrm{C}{f}$ y est en dessous de ses tangentes). Par conséquent, $f^{\prime}$ est croissante sur $[-2 ;-0,5]$, et $f^{\prime \prime}$ y est positive . Et $f^{\prime}$ est décroissante sur $[-0,5 ; 0,6]$, et $f^{\prime \prime}$ y est négative.

Exercice 6

$f(x)=4 e^{3 x-6}+2 x \operatorname{sur} I=\mathbb{R}$. Montrer que la tangente $t$ à $\mathrm{C}_{f}$ en 2 a pour équation $y=14 x-20$. Déterminer la convexité de la fonction $f$. Montrer que, pour tout $x$ de $\mathbb{R}$, on a : $e^{3 x-6} \geq 3 x-5$.

Corrigé

On calcule $f^{\prime}(x)$. $f(x)=4 e^{3 x-6}+2 x$ On pose $f=4 e^{u}+2 x$ avec $u=3 x-6$. D'où $f^{\prime}=4 u^{\prime} e^{u}+2$ avec $u^{\prime}=3$. Soit $f^{\prime}(x)=12 e^{3 x-6}+2$. On obtient alors: $f^{\prime}(2)=12 e^{0}+2=12+2=14$. Par ailleurs, on a: $f(2)=4 e^{0}+4=8$. Or la tangente $t$ à $\mathrm{C}_{f}$ en 2 a pour équation : $y=f(2)+f^{\prime}(2)(x-2)$. Donc $t$ a pour équation : $y=8+14(x-2)$. Soit : $y=14 x-20$.

On a vu que : $f^{\prime}(x)=12 e^{3 x-6}+2$. On calcule $f^{\prime \prime}(x)$. Comme ci-dessus, on obtient : $f^{\prime \prime}(x)=12 \times 3 e^{3 x-6}+0=36 e^{3 x-6}$. Or l'exponentielle $e^{3 x-6}$ est strictement positive et 36 également. Donc $f^{\prime \prime}$ est strictement positive. Et par là, $f$ est convexe sur $\mathbb{R}$.

Très souvent, les inégalités à démontrer après étude de la convexité utilisent la position de la courbe par rapport à ses tangentes. Comme $f$ est convexe sur $\mathbb{R}$, sa courbe représentative $\mathrm{C}_{f}$ y est au-dessus de toutes ses tangentes, en particulier au-dessus de la tangente $t$. Par conséquent, pour tout $x$ de $\mathbb{R}$, on a : $f(x) \geq 14 x-20$. Donc: $4 e^{3 x-6}+2 x \geq 14 x-20$. Donc : $4 e^{3 x-6} \geq 12 x-20$. Et donc : $e^{3 x-6} \geq 3 x-5$.

Exercice 7

Dans cet exercice, toute justification graphique est autorisée. La courbe C passe par les points $\mathrm{A}(-2 ; 3,5), \mathrm{B}(-1 ; 1)$, $\mathrm{C}(-0,5 ; 1,25), \mathrm{D}(0 ; 1,5), \mathrm{E}(0,8 ; 0)$ et $\mathrm{F}(1,-1)$.

1. Supposons que $C$ représente une fonction $f$ définie sur $[-2 ; 1]$.

Sur quel intervalle $f$ est-elle convexe? Déterminer le point d'inflexion de $f$. 2. Supposons que C représente la dérivée $g^{\prime}$ d'une fonction $g$ définie sur $[-2 ; 1]$.

Sur quel intervalle $g$ est-elle convexe ? Sur quel intervalle $g$ est-elle croissante ? 3. Supposons que C représente la dérivée seconde $h$ " d'une fonction $h$ définie sur [-2; 1]. Déterminer le point d'inflexion de $h$. Sur quel intervalle $h$ est-elle convexe?

Corrigé

1． C est au－dessus de ses tangentes entre A et C ．Elle est donc convexe sur l＇intervalle $[-2 ;-0,5]$ ．Elle est clairement concave entre C et F ．Le point d＇inflexion est le point C．

2．La dérivée $g^{\prime}$ est croissante entre B et D ．La fonction $g$ est donc convexe sur l＇intervalle $[-1 ; 0]$ ． La dérivée $g^{\prime}$ est positive entre A et E ．La fonction $g$ est donc croissante sur l＇intervalle ［－2；0，8］．

3．La dérivée seconde $h$＂s＇annule en changeant de signes en E．Donc la fonction $h$ admet le point d＇abscisse 0,8 comme point d＇inflexion． Attention！On ne connaît pas l＇ordonnée du point d＇inflexion． La dérivée seconde $h$＂est positive entre A et E ．Donc la fonction $h$ est convexe sur l＇intervalle $[-2 ; 0,8]$ ．

Exercice 8

Soit $f$ définie sur $\mathbb{R}$ par $f(x)=\frac{1}{4} x^{4}-x^{3}+2 x^{2}+5 x+7$ sur $\mathbb{R}$ ． Soit $d$ la tangente à $\mathrm{C}{f}$ en 0 ． La droite $d$ est en dessous de $\mathrm{C}{f}$ sur $\mathbb{R}$ ．Pourquoi？

Corrigé

Méthode 1 ：La position d＇une courbe par rapport à ses tangentes est liée à sa convexité．Étudions donc la convexité de $f$ ． On a：$f^{\prime}(x)=\frac{1}{4} \times 4 x^{3}-3 x^{2}+2 \times 2 x+5=x^{3}-3 x^{2}+4 x+5$ ． $f^{\prime \prime}(x)=3 x^{2}-3 \times 2 x+4=3 x^{2}-6 x+4$. $3 x^{2}-6 x+4$ est un trinôme avec $a=3, b=-6$ et $c=4$ ． $\Delta=b^{2}-4 a c=(-6)^{2}-4 \times 3 \times 4=-12$ ． $\Delta<0$ ．Le trinôme reste du signe de $a$ ，c＇est－à－dire positif． Finalement，$f^{\prime \prime}$ est strictement positive，et par là，$f$ est convexe． Et comme $f$ est convexe sur $\mathbb{R}$ ，sa courbe $\mathrm{C}{f}$ y est au－dessus de ses tangentes． C＇est vrai en particulier pour la tangente $d$ ，qui sera donc en dessous de $\mathrm{C}{f}$ sur $\mathbb{R}$ ．

Méthode 2 ：Utilisons l＇équation de $d$ ．

$f^{\prime}(x)=\frac{1}{4} \times 4 x^{3}-3 x^{2}+2 \times 2 x+5=x^{3}-3 x^{2}+4 x+5$ ．

Donc $f^{\prime}(0)=5$. Or $f(0)=7$. Donc $d$ a pour équation : $y=f(0)+f^{\prime}(0)(x-0)$, soit : $y=7+5(x-0)$, soit : $y=5 x+7$.

Étudions alors le signe de la différence : $g(x)=f(x)-(5 x+7)$. Pour montrer que $d$ est en dessous de $\mathrm{C}{f}$ sur $\mathbb{R}$, il suffit de montrer que $g(x) \geq 0$ pour tout $x$. On a: $g(x)=\frac{1}{4} x^{4}+x^{3}+2 x^{2}+5 x+7-5 x-7=\frac{1}{4} x^{4}+x^{3}+2 x^{2}$ Pour étudier le signe de ce polynôme, il suffit de le factoriser. On obtient: $g(x)=x^{2}\left(\frac{1}{4} x^{2}+x+2\right)$ Le carré $x^{2}$ est nul en 0 et strictement positif ailleurs. Le trinôme $\frac{1}{4} x^{2}+x+2$ a pour discriminant $\Delta=1^{2}-4 \times \frac{1}{4} \times 2=-1$. $\Delta<0$. Le trinôme reste du signe de son coefficient dominant $\frac{1}{4}$, c'est-à-dire positif. Finalement, le produit $g(x)$ est nul en 0 et strictement positif ailleurs. Par conséquent, $d$ est bien en dessous de $\mathrm{C}{f}$ sur $\mathbb{R}$.

Chacun aura remarqué que la première méthode est nettement plus rapide !

Exercice 9

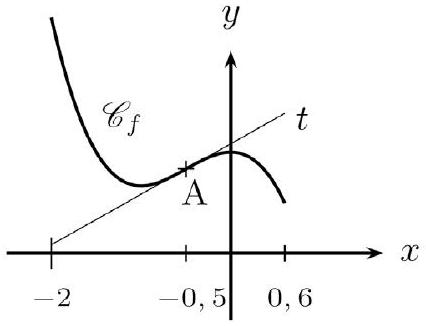
Soit $f$ définie sur $\mathbb{R}$ par $f(x)=-x^{3}-1.5 x^{2}+1,5$.

• Étudier la convexité de la fonction $f$.
• Déterminer le point d'inflexion A de $\mathrm{C}_{f}$.
• Montrer que la tangente $t$ à $\mathrm{C}_{f}$ au point A admet pour équation $y=0,75 x+1,625$
• Sans calcul, prouver que $f(0,6) \leq 0,75 \times 0,6+1,625$.
• Tracer rapidement l'allure de $\mathrm{C}_{f}$ et de $t$ sur l'intervalle $[-2 ; 0,6]$.

Placer A sur le dessin.

Corrigé

• $f^{\prime}(x)=-3 x^{2}-1,5 \times 2 x+0=-3 x^{2}-3 x$. $f^{\prime \prime}(x)=-3 \times 2 x-3=-6 x-3$. $-6 x-3$ est une fonction affine qui s'annule pour $x=-0,5$. De plus, son coefficient directeur -6 est strictement négatif. D'où le tableau de signes de $f^{\prime \prime}$ ci-après.

$x$	$-\infty$	$-0,5$	$+\infty$
$f^{\prime \prime}(x)$	+0	-

Par conséquent, $f$ est convexe sur $]-\infty ;-0,5]$ et concave sur $[-0,5 ;+\infty[$.

• $f^{\prime \prime}$ s'annule en $-0,5$ en changeant de signe, par conséquent, $\mathrm{C}_{f}$ admet un point d'inflexion A en - 0,5 . Comme $f(-0,5)=1,25$, le point d'inflexion A a pour coordonnées $(-0,5 ; 1,25)$
• La tangente $t$ à $\mathrm{C}{f}$ en $x{0}$ a pour équation $y=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)$. ici : $x_{0}=-0,5, f\left(x_{0}\right)=1,25, f^{\prime}\left(x_{0}\right)=-3 \times(-0,5)^{2}-3 \times(-0,5)=0,75$. D'où l'équation : $y=1,25+0,75(x-(-0,5))$. Soit : $y=1,25+0,75 x+0,375$. Soit : $y=0,75 x+1,625$.
• On a vu que $f$ est concave sur $[-0,5 ;+\infty[$. Donc elle y est en dessous de ses tangentes. C'est vrai en particulier en 0,6 , et pour la tangente $t$ en $-0,5$. Donc, pour $x=0,6$, l'ordonnée du point de $\mathrm{C}_{f}$ est inférieure à celle du point de $t$. Et par là : $f(0,6) \leq 0,75 \times 0,6+1,625$.
• Graphique ci-après.