Cours : Intégrales

8
Intégrales

I/ Cas des fonctions continues et positives

I.a/ Intégrales et aires

Définition

Soit $f$ une fonction continue et positive sur un intervalle $[a ; b]$. Soit $C$ la courbe représentative de $f$ dans un repère orthogonal (les axes sont perpendiculaires). L'aire (en unités d'aires) du domaine D délimité par la courbe $C$, l'axe des abscisses et les droites d'équations $x=a$ et $x=b$ se note : $\int_{a}^{b} f(t) d t$. $\int_{a}^{b} f(t) d t$ se dit : «intégrale de $a$ à $b$ de $f(t) d t$ »

b. Intégrales et primitives

Propriété

Si $f$ est une fonction continue et positive sur un intervalle $[a ; b]$. Alors la fonction $F_{a}$ définie sur $[a ; b]$ par $\quad F_{a}(x)=\int_{a}^{x} f(t) d t \quad$ est la primitive de $f$ qui s'annule en $a$.

Propriété

Soit $f$ une fonction continue et positive sur un segment $[a ; b]$. Soit F une primitive quelconque de $f$ sur I .

On a alors l'égalité : $\int_{a}^{b} f(t) d t=F(b)-F(a)$ On note également : $\quad \int_{a}^{b} f(t) d t=[F(t)]_{a}^{b}$.

II Cas des fonctions continues

a. Intégrales et primitives

Propriété

Toute fonction continue sur un intervalle admet des primitives.

Définition

Soit $f$ une fonction continue de signe quelconque sur un intervalle I contenant les réels $a$ et $b$. Soit F une primitive quelconque de $f$ sur I. Alors $\int_{a}^{b} f(t) d t$ est définie par l'égalité :

$$ \int_{a}^{b} f(t) d t=F(b)-F(a) $$

On note également : $\quad \int_{a}^{b} f(t) d t=[F(t)]{a}^{b}$. On notera que la fonction $f$ peut être positive, ou négative, ou de signe variable, et que les réels a et $b$ sont dans un ordre quelconque. On notera également que, pour tout $x$ de $I, F{a}(x)=\int_{a}^{x} f(t) d t$ est, comme au paragraphe I, la primitive de $f$ qui s'annule en a.

b. Valeur moyenne

Définition

Soit $f$ une fonction continue sur un intervalle $[a ; b]$. La valeur moyenne de $f$ sur $[a ; b]$ est le nombre réel $\quad m=\frac{1}{b-a} \int_{a}^{b} f(t) d t$.

Propriété

Soit $f$ une fonction continue et positive sur un intervalle $[a ; b]$, de valeur moyenne $m$ sur $[a ; b]$. Soit $C$ la courbe représentative de $f$ dans un repère orthogonal. Le rectangle de côtés $m$ et $b-a$ a même aire que le domaine situé sous la courbe $C$.

c. Propriétés

Linéarité

Soit $f$ et $g$ deux fonctions continues sur un intervalle contenant les réels $a$ et $b$, et $k$ un nombre réel, alors : $\quad \int_{a}^{b}(f(t)+g(t)) d t=\int_{a}^{b} f(t) d t+\int_{a}^{b} g(t) d t$ et : $\quad \int_{a}^{b}(k f(t)) d t=k \int_{a}^{b} f(t) d t$ En particulier, on obtient :

$$ \int_{a}^{b}(f(t)-g(t)) d t=\int_{a}^{b} f(t) d t-\int_{a}^{b} g(t) d t $$

Aire entre deux courbes

Soit $f$ et $g$ deux fonctions continues sur un intervalle $[a ; b]$. Si $g \leq f$ sur $[a ; b]$, alors $\int_{a}^{b}(f(t)-g(t)) d t$ est l'aire du domaine situé entre les deux courbes $\mathrm{C}{f}$ et $\mathrm{C}{g}$ (quel que soit le signe des fonctions $f$ et $g$ ).

Relation de Chasles

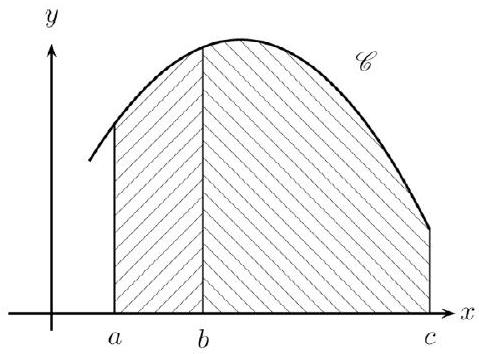
Soit $f$ une fonction continue sur un intervalle contenant les réels $a, b$ et $c$. Alors : $\quad \int_{a}^{b} f(t) d t+\int_{b}^{c} f(t) d t=\int_{a}^{c} f(t) d t$. Si, de plus, $f$ est positive, et si $a<b<c$, alors cette propriété traduit l'additivité des aires : l'aire sous la courbe entre $a$ et $c$ est la somme de l'aire sous la courbe entre $a$ et $b$ et de l'aire sous la courbe entre $b$ et $c$.

Positivité

Soit $f$ une fonction continue sur un intervalle $[a ; b]$. Si $f \geq 0$ sur $[a ; b]$, alors : $\int_{a}^{b} f(t) d t \geq 0$. Si $f \leq 0$ sur $[a ; b]$, alors : $\int_{a}^{b} f(t) d t \leq 0$.

Comparaison

Soient $f$ et $g$ deux fonctions continues sur un intervalle $[a ; b]$. Si $f \leq g$ sur $[a ; b]$, alors : $\quad \int_{a}^{b} f(t) d t \leq \int_{a}^{b} g(t) d t$. Si, de plus, $f$ et $g$ sont positives, alors cette propriété traduit le fait que l'aire sous la courbe de $f$ est inférieure à celle située sous la courbe de $g$.

d. Intégration par parties

Intégration par parties

Soit I un intervalle contenant les réels $a$ et $b$. Soit $u$ et $v$ deux fonctions dérivables sur I, dont les dérivées $u^{\prime}$ et $v^{\prime}$ sont également continues sur I. Alors : $\quad \int_{a}^{b} u^{\prime}(t) v(t) d t=[u(t) v(t)]{a}^{b}-\int{a}^{b} u(t) v^{\prime}(t) d$ $t$

On note souvent : $\int_{a}^{b} u^{\prime} v d t=[u v]{a}^{b}-\int{a}^{b} u v^{\prime} d t$.