Exercices corrigés

Exercices corrigés

Exercice 1

Un exercice graphique à savoir faire absolument.

1. Conjecturer la valeur de $\lim _{x \rightarrow+\infty} f(x)$.
2. Conjecturer la valeur chacune des limites suivantes, et donner, s'il y a lieu, l'équation réduite de l'asymptote associée. $\lim _{x \rightarrow-\infty} f(x)$ $\lim _{x \rightarrow-2} f(x)$ $x<-2$ $\lim _{x \rightarrow-2} f(x)$ $x>-2$

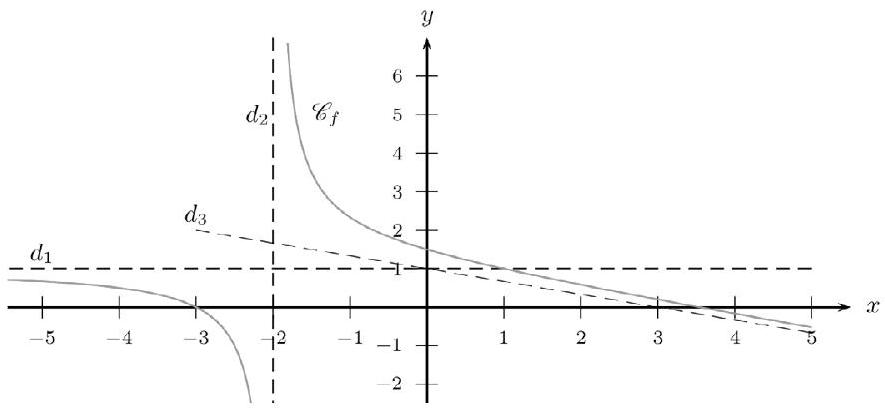
Corrigé

1. Comme $x$ tend vers $+\infty$, on considère un point $M$ sur la partie droite de $\mathrm{C}_{f}$, et on déplace $M$ vers la droite. On regarde vers quoi tend l'ordonnée de $M$. On conjecture que $\lim _{x \rightarrow+\infty} f(x)=-\infty$.
2. Comme $x$ tend vers $-\infty$, on considère un point $M$ sur la partie gauche de $\mathrm{C}_{f}$, et on déplace $M$ vers la gauche.

On regarde vers quoi tend l'ordonnée de $M$. On conjecture que $\lim _{x \rightarrow-\infty} f(x)=1$ .

Donc la droite d'équation $y=1$ est asymptote horizontale à $\mathrm{C}_{f}$ .

Comme $x$ tend vers -2 en restant inférieur à -2 , on considère un point $M$ sur la partie gauche de $\mathrm{C}_{f}$, et on déplace $M$ vers la droite. On regarde vers quoi tend l'ordonnée de M.

On conjecture que $\lim _{\substack{x \rightarrow-2 \ x<-2}} f(x)=-\infty$ .

Donc la droite d'équation $x=-2$ est asymptote verticale à $\mathrm{C}_{f}$.

Comme $x$ tend vers $-2$ en restant supérieur à $-2$ , on considère un point $M$ sur la partie droite de $\mathrm{C}_{f}$, et on déplace $M$ vers la gauche. On regarde vers quoi tend l'ordonnée de M. On conjecture que $\lim _{x \rightarrow-2} f(x)=+\infty$. $\quad$ $x>-2$

Donc la droite d'équation $x=-2$ est asymptote verticale à $\mathrm{C}_{f}$.

Exercice 2

Un exercice classique sur les calculs de limites.

1. Soit $f$ la fonction définie par $f(x)=x^{2}+x+\frac{19}{x}$ pour tout réel $x$ non nul.

Déterminer $\lim _{x \rightarrow+\infty} f(x)$ et $\lim _{x \rightarrow-\infty} f(x)$. 2. Soit $f$ la fonction définie par $f(x)=\frac{x-1}{x^{2}+7}+5$ pour tout réel $x$.

Déterminer $\lim {x \rightarrow+\infty} f(x)$. En déduire une éventuelle asymptote de la courbe $\mathrm{C}{f}$. 3. Soit $f$ la fonction définie par $f(x)=\sqrt{x^{2}-x+9}$ pour tout réel $x$.

Déterminer $\lim _{x \rightarrow+\infty} f(x)$.

Corrigé

1. $f(x)=x^{2}+x+\frac{19}{x}$.

Comme $\lim _{x \rightarrow+\infty} x^{2}=+\infty, \lim _{x \rightarrow+\infty} x=+\infty$, et $\lim _{x \rightarrow+\infty} \frac{19}{x}=0$, on obtient: $\lim _{x \rightarrow+\infty} f(x)=+\infty$ (limite d'une somme).

On obtient facilement $\lim _{x \rightarrow-\infty} x^{2}=+\infty$ et $\lim _{x \rightarrow-\infty} x=-\infty$, ce qui conduit à une forme indéterminée. On factorise alors le terme «dominant» de la somme $x^{2}+x$. On a : $x^{2}+x=x^{2}\left(1+\frac{1}{x}\right)$. Or $\lim _{x \rightarrow-\infty} x^{2}=+\infty$, et $\lim _{x \rightarrow-\infty} 1+\frac{1}{x}=1+0=1$. Donc $\lim _{x \rightarrow-\infty} x^{2}+x=+\infty$ (limite d'un produit).

Par ailleurs $\lim _{x \rightarrow-\infty} \frac{19}{x}=0$. Donc $\lim _{x \rightarrow-\infty} f(x)=+\infty$ (limite d'une somme). 2. $f(x)=\frac{x-1}{x^{2}+7}+5$.

On obtient facilement $\lim _{x \rightarrow+\infty} x-1=+\infty$ et $\lim _{x \rightarrow+\infty} x^{2}+7=+\infty$, ce qui conduit à une forme indéterminée. On factorise alors les termes «dominants» du quotient et on simplifie. $f(x)=\frac{x\left(1-\frac{1}{x}\right)}{x^{2}\left(1+\frac{7}{x^{2}}\right)}+5=\frac{1}{x} \frac{1-\frac{1}{x}}{1+\frac{7}{x^{2}}}+5$. $\lim {x \rightarrow+\infty} f(x)=0 \times \frac{1-0}{1+0}+5=5$ (opérations sur les limites). Donc la droite horizontale d'équation $y=5$ est une asymptote de la courbe $\mathrm{C}{f}$ en $+\infty$. 3. $f(x)=\sqrt{x^{2}-x+9}$.

On obtient facilement $\lim _{x \rightarrow+\infty} x^{2}=+\infty$ et $\lim _{x \rightarrow+\infty}-x=-\infty$, ce qui conduit à une forme indéterminée. On factorise alors le terme «dominant» de la somme $x^{2}-x+9$. $x^{2}-x+9=x^{2}\left(1-\frac{1}{x}+\frac{9}{x^{2}}\right)$. Comme $\lim _{x \rightarrow+\infty} x^{2}=+\infty$ et $\lim _{x \rightarrow+\infty} 1-\frac{1}{x}+\frac{9}{x^{2}}=1-0+0=1$, on obtient: $\lim _{x \rightarrow+\infty} x^{2}-x+9=+\infty$. Or : $\lim _{y \rightarrow+\infty} \sqrt{y}=+\infty$. Donc : $\lim _{x \rightarrow+\infty} f(x)=+\infty$ (limite d'une composée).

Exercice 3

Un exercice classique sur les calculs de limites.

1. Soit $g$ la fonction définie par $g(x)=\frac{8}{1+2 e^{-0,04 x}}$ pour tout réel $x$.

Déterminer $\lim _{x \rightarrow+\infty} g(x)$ et $\lim _{x \rightarrow-\infty} g(x)$. 2. Soit $f$ la fonction définie par $f(x)=(x+1) e^{x}$ pour tout réel $x$.

Déterminer $\lim _{x \rightarrow+\infty} f(x)$ et $\lim {x \rightarrow-\infty} f(x)$. En déduire les éventuelles asymptotes de la courbe $\mathrm{C}{f}$. 3. Soit $f$ la fonction définie par $f(x)=(x+2) e^{-x}$ pour tout réel $x$.

Déterminer $\lim _{x \rightarrow+\infty} f(x)$ et $\lim {x \rightarrow-\infty} f(x)$. En déduire les éventuelles asymptotes de la courbe $\mathrm{C}{f}$. 4. Soit $f$ la fonction définie par $f(x)=3 x e^{-\frac{1}{4} x}+5$ pour tout réel $x$.

Déterminer $\lim _{x \rightarrow+\infty} f(x)$. Interpréter le résultat.

Corrigé

1. $g(x)=\frac{8}{1+2 e^{-0,04 x}}$

Comme $\lim _{x \rightarrow+\infty}-0,04 x=-\infty$ et $\lim _{y \rightarrow-\infty} e^{y}=0$, on obtient $\lim _{x \rightarrow+\infty} e^{-0,04 x}=0$ (limite d'une composée). D'où $\lim _{x \rightarrow+\infty} g(x)=\frac{8}{1+2 \times 0}=8$.

Comme $\lim _{x \rightarrow-\infty}-0,04 x=+\infty$ et $\lim _{y \rightarrow+\infty} e^{y}=+\infty$, on obtient $\lim _{x \rightarrow+\infty} e^{-0,04 x}=+\infty$ (limite d'une composée). D'où $\lim _{x \rightarrow+\infty} 1+2 e^{-0,04 x}=+\infty$. Et par là $\lim _{x \rightarrow-\infty} g(x)=0$ (limite d'un quotient). 2. $f(x)=(x+1) e^{x}$.

Comme $\lim _{x \rightarrow+\infty} x+1=+\infty$ et $\lim _{x \rightarrow+\infty} e^{x}=+\infty$, on obtient $\lim _{x \rightarrow+\infty} f(x)=+\infty$.

On obtient facilement $\lim _{x \rightarrow-\infty} x+1=-\infty$ et $\lim _{x \rightarrow-\infty} e^{x}=0$, ce qui conduit à une forme indéterminée. On développe alors le produit $f(x)$. $f(x)=x e^{x}+e^{x}$. Comme $\lim _{x \rightarrow-\infty} x e^{x}=0$ et $\lim _{x \rightarrow-\infty} e^{x}=0$, on obtient $\lim {x \rightarrow-\infty} f(x)=0$ (limite d'une somme). Donc la droite horizontale d'équation $y=0$ (l'axe des abscisses) est une asymptote de la courbe $\mathrm{C}{f}$ en $-\infty$. 3. $f(x)=(x+2) e^{-x}$.

Comme $\lim _{x \rightarrow+\infty}-x=-\infty$ et $\lim _{y \rightarrow-\infty} e^{y}=0$, on obtient $\lim _{x \rightarrow+\infty} e^{-x}=0$.

On obtient facilement $\lim _{x \rightarrow+\infty} x+2=+\infty$. Comme $\lim _{x \rightarrow+\infty} e^{-x}=0$, cela conduit à une forme indéterminée. On développe alors le produit $f(x)$. $f(x)=x e^{-x}+2 e^{-x}=-\left(-x e^{-x}\right)+2 e^{-x}$. Comme $\lim _{x \rightarrow+\infty}-x=-\infty$ et $\lim _{y \rightarrow-\infty} y e^{y}=0$, on obtient $\lim _{x \rightarrow+\infty}-x e^{-x}=0$. Donc $\lim {x \rightarrow+\infty} f(x)=-0+2 \times 0=0$. Donc la droite horizontale d'équation $y=0$ (l'axe des abscisses) est une asymptote de la courbe $\mathrm{C}{f}$ en $+\infty$.

Comme $\lim _{x \rightarrow-\infty}-x=+\infty$ et $\lim _{y \rightarrow+\infty} e^{y}=+\infty$, on obtient $\lim _{x \rightarrow-\infty} e^{-x}=+\infty$. Par ailleurs : $\lim _{x \rightarrow-\infty} x+2=-\infty$. D'où : $\lim _{x \rightarrow-\infty} f(x)=-\infty$ (limite d'un produit). 4. $f(x)=3 x e^{-\frac{1}{4} x}+5$.

Comme $\lim _{x \rightarrow+\infty}-\frac{1}{4} x=-\infty$ et $\lim _{y \rightarrow-\infty} e^{y}=0$, on obtient $\lim _{x \rightarrow+\infty} e^{-\frac{1}{4} x}=0$. Mais comme $\lim _{x \rightarrow+\infty} 3 x=+\infty$, cela conduit à une forme indéterminée. On fait apparaître $-\frac{1}{4} x$ devant l'exponentielle pour utiliser la limite de $y e^{y}$ en $-\infty$. On a: $f(x)=-12 \times-\frac{1}{4} x e^{-\frac{1}{4} x}+5$. Comme $\lim _{x \rightarrow+\infty}-\frac{1}{4} x=-\infty$ et $\lim _{y \rightarrow-\infty} y e^{y}=0$, on obtient $\lim _{x \rightarrow+\infty}-\frac{1}{4} x e^{-\frac{1}{4} x}=0$. Par conséquent : $\lim {x \rightarrow+\infty} f(x)=-12 \times 0+5=5$. Donc la droite horizontale d'équation $y=5$ est une asymptote de la courbe $\mathrm{C}{f}$ en $+\infty$.

Exercice 4

Un exercice classique sur les calculs de limites.

Attention! Cet exercice utilise la fonction logarithme népérien.

1. Soit $h$ la fonction définie par $h(x)=\frac{1+\ln x}{x^{2}}$ sur $] 0 ;+\infty[$.

Déterminer $\lim _{x \rightarrow 0} h(x)$ et $\lim _{x \rightarrow+\infty} h(x)$. 2. Soit $f$ la fonction définie par $f(x)=\frac{1+2 \ln x}{x}$ sur $] 0 ;+\infty[$.

Déterminer $\lim _{x \rightarrow 0} f(x)$ et $\lim {x \rightarrow+\infty} f(x)$. En déduire les éventuelles asymptotes de la courbe $\mathrm{C}{f}$.

Corrigé

1. $h(x)=\frac{1+\ln x}{x^{2}}$.

On a: $\lim _{x \rightarrow 0} \ln x=-\infty$, et donc : $\lim _{x \rightarrow 0} 1+\ln x=-\infty$. Par ailleurs: $\lim _{x \rightarrow 0} x^{2}=0$ et $x^{2}$ reste strictement positif. Donc $\lim _{x \rightarrow 0} h(x)=-\infty$ (limite d'un quotient).

On obtient facilement $\lim _{x \rightarrow+\infty} 1+\ln x=+\infty$ et $\lim _{x \rightarrow+\infty} x^{2}=+\infty$, ce qui conduit à une forme indéterminée. On factorise alors le terme dominant du numérateur. $h(x)=\frac{\ln x}{x} \frac{1+\frac{1}{\ln x}}{x}$. Examinons le facteur de gauche. On a : $\lim _{x \rightarrow+\infty} \frac{\ln x}{x}=0$. Examinons le facteur de droite. Tout d'abord : $\lim _{x \rightarrow+\infty} 1+\frac{1}{\ln x}=1+0=1$. Et donc, comme $\lim _{x \rightarrow+\infty} x=+\infty$, on obtient : $\lim _{x \rightarrow+\infty} \frac{1+\frac{1}{\ln x}}{x}=0$. Donc, finalement : $\lim _{x \rightarrow+\infty} h(x)=0 \times 0=0$ (limite d'un produit) 2. $f(x)=\frac{1+2 \ln x}{x}$.

On a: $\lim _{x \rightarrow 0} \ln x=-\infty$, et donc : $\lim _{x \rightarrow 0} 1+2 \ln x=-\infty$. Par ailleurs : $\lim _{x \rightarrow 0} x=0$ et $x$ reste strictement positif (sur $] 0 ;+\infty[$ ). Donc $\lim {x \rightarrow 0} h(x)=-\infty$ (limite d'un quotient). Donc la droite verticale d'équation $x=0$ (l'axe des ordonnées) est une asymptote de la courbe $\mathrm{C}{f}$ en 0 .

On obtient facilement $\lim _{x \rightarrow+\infty} 1+2 \ln x=+\infty$ et $\lim _{x \rightarrow+\infty} x=+\infty$, ce qui conduit à une forme indéterminée. On factorise alors le terme dominant du numérateur. $h(x)=\frac{\ln x}{x}\left(1+\frac{1}{\ln x}\right)$. Examinons le facteur de gauche. On a : $\lim _{x \rightarrow+\infty} \frac{\ln x}{x}=0$. Examinons le facteur de droite. $\lim _{x \rightarrow+\infty} 1+\frac{1}{\ln x}=1+0=1$. Donc, finalement: $\lim {x \rightarrow+\infty} h(x)=0 \times 0=0$ (limite d'un produit). Donc la droite horizontale d'équation $y=0$ (l'axe des abscisses) est une asymptote de la courbe $\mathrm{C}{f}$ en $+\infty$.

Exercice 5

Un exercice sur les limites utilisant des fonctions circulaires.

1. Soit $g$ la fonction définie par $g(x)=x^{2}-\frac{\cos x}{x}$ sur $\left.I=\right] 0 ;+\infty[$.

Déterminer par comparaison $\lim _{x \rightarrow+\infty} g(x)$. 2. Soit $h$ la fonction définie par $h(x)=\frac{1}{x \cos x}$ sur $\left.\left.I=\right] 0 ; \frac{\pi}{4}\right]$.

Déterminer par comparaison $\lim _{x \rightarrow 0} h(x)$.

Corrigé

L'expression «par comparaison» signifie qu'il faut utiliser le théorème de comparaison ou le théorème des gendarmes.

1. Pour tout réel $x$, on a : $-1 \leq \cos x \leq 1$, et par là : $\frac{-1}{x} \leq \frac{\cos x}{x} \leq \frac{1}{x}$.

Le sens des inégalités n'a pas changé car $x$ est strictement positif. Or, comme $\lim _{x \rightarrow+\infty} \frac{-1}{x}=0$ et $\lim _{x \rightarrow+\infty} \frac{1}{x}=0$, on obtient, d'après le théorème des gendarmes : $\lim _{x \rightarrow+\infty} \frac{\cos x}{x}=0$. Par ailleurs, on a : $\lim _{x \rightarrow+\infty} x^{2}=+\infty$. Donc, finalement, on obtient $\lim _{x \rightarrow+\infty} g(x)=+\infty$ (limite d'une somme). 2. Pour tout réel $x$ dans $\left.] 0 ; \frac{\pi}{4}\right]$, on a : $\cos 0 \geq \cos x \geq \frac{\pi}{4}$ (car la fonction cosinus est décroissante sur cet intervalle). Soit: $1 \geq \cos x \geq \frac{\sqrt{2}}{2}$.

Et par là : $x \geq x \cos x \geq x \frac{\sqrt{2}}{2}$. Le sens des inégalités n'a pas changé car $x$ est strictement positif. Et finalement: $\frac{1}{x} \leq \frac{1}{x \cos x} \leq \frac{1}{x} \frac{2}{\sqrt{2}}$ (le sens des inégalités a changé car la fonction inverse est décroissante sur $\mathbb{R}_{+}^{*}$ ). On obtient en particulier : $\frac{1}{x} \leq \frac{1}{x \cos x}$. Or : $\lim _{x \rightarrow 0} \frac{1}{x}=+\infty(\operatorname{car} x$ reste strictement positif dans $I)$. On obtient donc, par comparaison : $\lim _{x \rightarrow 0} h(x)=+\infty$.