Cours : Vecteurs, droites et plans de l'espace

Vecteurs, droites
et plans de l'espace

I Droites et plans de l'espace

Remarque : quelques mises au point pour commencer avant de manipuler les vecteurs de l'espace...

Propriété

Deux droites de l'espace sont : soit coplanaires (dans un même plan), soit non coplanaires.

Deux droites coplanaires sont : soit parallèles, soit sécantes .

Deux droites parallèles sont : soit strictement parallèles, soit confondues.

Propriété

Une droite et un plan de l'espace sont : soit sécants selon un point, soit parallèles .

Une droite et un plan parallèles sont : soit strictement parallèles, soit tels que la droite est dans le plan.

Propriété

Deux plans de l'espace sont : soit sécants selon une droite, soit parallèles .

Deux plans parallèles sont : soit strictement parallèles, soit confondus .

II Vecteurs de l'espace

Remarque : les définitions et propriétés relatives aux vecteurs du plan s'étendent à l'espace. En voici quelques-unes.

Propriété

ABDC est un parallélogramme si et seulement si $\overrightarrow{A B}=\overrightarrow{C D}$.

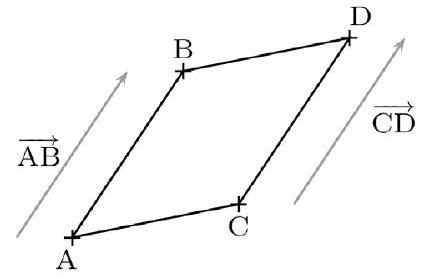
ABDC est un parallélogramme si et seulement si D est l'image de C par la translation de vecteur $\overrightarrow{A B}$.

Propriété

Règle du parallélogramme :

ABDC est un parallélogramme si et seulement si $\overrightarrow{A B}+\overrightarrow{A C}=\overrightarrow{A D}$.

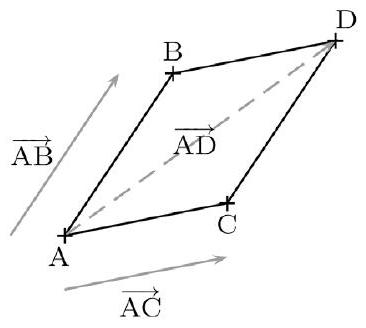
Propriété

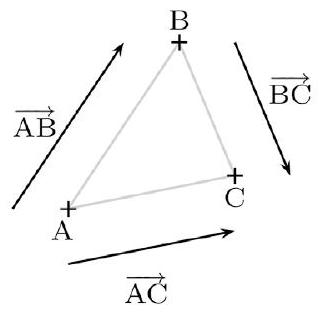
Relation de Chasles :

$\overrightarrow{A B}+\overrightarrow{B C}=\overrightarrow{A C}$.

Propriété

Milieu et vecteurs opposés : Le point I est le milieu de $[\mathrm{AB}]$ si et seulement si $\overrightarrow{A I}=-\overrightarrow{B I}$.

III Combinaisons linéaires et bases

a. Combinaisons linéaires

Définition

Si $\overrightarrow{u_{1}}, \overrightarrow{u_{2}}, \ldots, \overrightarrow{u_{n}}$ sont $n$ vecteurs, et si $a_{1}, a_{2}, \ldots, a_{n}$ sont $n$ réels, alors le vecteur $a_{1} \cdot \overrightarrow{u_{1}}+a_{2} \cdot \overrightarrow{u_{2}}+\ldots+a_{n} \cdot \overrightarrow{u_{n}}$ est une combinaison linéaire des vecteurs $\overrightarrow{u_{1}}, \overrightarrow{u_{2}}$, $\ldots$ et $\overrightarrow{u_{n}}$.

b. Les droites de l'espace

Définition

Le vecteur nul $\overrightarrow{0}$ est colinéaire à tout vecteur. Deux vecteurs non nuls $\vec{u}$ et $\vec{v}$ sont colinéaires si et seulement si il existe un réel $k$ tel que $\vec{v}=k \cdot \vec{u}$.

Propriétés et définitions

Soient A et B deux points distincts. M appartient à la droite ( AB ) si et seulement si il existe un nombre réel $k$ tel que $\overrightarrow{A M}=k \overrightarrow{A B}$. $\overrightarrow{A B}$ est un vecteur directeur de la droite (AB).

Remarque :

Une droite peut être définie :

• ou bien par 2 points distincts,
• ou bien par un point et un vecteur directeur (nécessairement non nul).

Définitions et propriétés

On considère une droite de vecteur directeur $\vec{u}$. La direction (vectorielle) D de cette droite est l'ensemble de tous les vecteurs colinéaires à $\vec{u}$. $\vec{v}$ appartient à D si et seulement si il existe un réel $k$ tel que $\vec{v}=k \cdot \vec{u}$. Le vecteur $\vec{u}$ constitue alors une base de la direction vectorielle D . Le réel $k$ est unique et s'appelle la coordonnée de $\vec{v}$ dans la base $\vec{u}$.

Propriété

On considère deux droites de vecteurs directeurs respectifs $\vec{u}$ et $\vec{v}$. Ces droites sont parallèles : si et seulement si elles ont la même direction (vectorielle), si et seulement si $\vec{u}$ et $\vec{v}$ sont colinéaires.

c. Les plans de l'espace

Propriétés et définitions

Soient $\mathrm{A}, \mathrm{B}$ et C trois points non alignés. M appartient au plan (ABC) si et seulement si il existe deux nombres réels $x$ et $y$ tels que $\overrightarrow{A M}=x \overrightarrow{A B}+y \overrightarrow{A C}$. Le couple $(\overrightarrow{A B}, \overrightarrow{A C})$ est un couple de vecteurs directeurs du plan (ABC).

Remarque :

Un plan peut être défini :

• ou bien par 3 points non alignés,
• ou bien par un point et deux vecteurs directeurs (nécessairement non colinéaires).

Définitions et propriétés

On considère un plan de vecteurs directeurs $\vec{u}$ et $\vec{v}$. La direction (vectorielle) $P$ de ce plan est l'ensemble de tous les vecteurs combinaisons linéaires de $\vec{u}$ et de $\vec{v}$. $\vec{w}$ appartient à P si et seulement si il existe deux réels $a$ et $b$ tel que $\vec{w}=a \cdot \vec{u}+b \cdot \vec{v}$. Le couple de vecteurs $(\vec{u}, \vec{v})$ constitue alors une base du plan vectoriel P .

Le couple de réels $(a, b)$ est unique et s'appelle les coordonnées de $\vec{w}$ dans la base $(\vec{u}, \vec{v})$.

Remarque.

Par abus de langage, il est fréquent de confondre un plan et sa direction vectorielle.

Propriétés

On considère deux plans de couples de vecteurs directeurs respectifs $(\vec{u}, \vec{v})$ et $\left(\overrightarrow{u^{\prime}}, \overrightarrow{v^{\prime}}\right)$. Ces plans sont parallèles : si et seulement si ils ont la même direction (vectorielle), si et seulement si $\overrightarrow{u^{\prime}}$ et $\overrightarrow{v^{\prime}}$ sont chacun combinaison linéaire de $\vec{u}$ et $\vec{v}$. On considère une droite de vecteur directeur $\vec{u}$ et un plan de direction vectorielle $P$. La droite est parallèle au plan : si et seulement si la direction (vectorielle) de la droite est incluse dans celle du plan, si et seulement si $\vec{u}$ appartient à la direction vectorielle P .

Définition

Les points $A, B, C$ et $D$ sont coplanaires si et seulement si ils appartiennent à un même plan. Les vecteurs $\vec{u}, \vec{v}$ et $\vec{w}$ sont coplanaires : si et seulement si ils appartiennent à une même direction vectorielle de plan. Les vecteurs $\vec{u}, \vec{v}$ et $\vec{w}$ sont linéairement indépendants : si et seulement si ils ne sont pas coplanaires.

Propriété

Si $\vec{u}$ et $\vec{v}$ sont deux vecteurs non colinéaires, alors : les vecteurs $\vec{u}, \vec{v}$ et $\vec{w}$ sont coplanaires si et seulement si il existe des nombres réels $x$ et $y$ tels que $\vec{w}=x \vec{u}+y \vec{v}$.

d. Les bases de l'espace

Propriété

Les trois vecteurs $\vec{u}, \vec{v}$ et $\vec{w}$ sont linéairement indépendants (c'est-à-dire non coplanaires) : si et seulement si $a \vec{u}+b \vec{v}+c \vec{w}=\overrightarrow{0}$ implique que $a=b=c=0$.

Définition

Trois vecteurs non coplanaires $\vec{\imath}, \vec{\jmath}$ et $\vec{k}$ définissent une base de l'espace (vectoriel), notée $(\vec{\imath}, \vec{\jmath}, \vec{k})$. Un point O et trois vecteurs non coplanaires $\vec{\imath}, \vec{\jmath}$ et $\vec{k}$ définissent un repère de l'espace, noté ( $O, \vec{\imath}, \vec{\jmath}, \vec{k}$ ).

Définition et propriété

Soient $(\vec{l}, \vec{\jmath}, \vec{k})$ une base de l'espace. Pour tout vecteur $\vec{v}$, il existe un triplet ( $x ; y ; z$ ) de nombres réels tel que $\vec{v}=x \vec{\imath}+y \vec{\jmath}+z \vec{k}$. Le triplet de réels $(x, y, z)$ est unique et s'appelle les coordonnées de $\vec{v}$ dans la base $(\vec{\imath}, \vec{\jmath}, \vec{k})$. $x$ est l'abscisse de $\vec{v}$. $y$ est l'ordonnée de $\vec{v}$. $z$ est la cote de $\vec{v}$.

Définition et propriété

Soient $(O, \vec{\imath}, \vec{\jmath}, \vec{k})$ un repère de l'espace. Pour tout point M, il existe un triplet ( $x ; y ; z$ ) de nombres réels tel que $\overrightarrow{O M}=x \vec{\imath}+y \vec{\jmath}+z \vec{k}$. Le triplet de réels ( $x, y, z$ ) est unique et s'appelle les coordonnées de M dans le repère ( $0, \vec{\imath}, \vec{\jmath}, \vec{k}$ ). $x$ est l'abscisse de M. $y$ est l'ordonnée de M. $z$ est la cote de M.

Propriété

Soient $(O, \vec{\imath}, \vec{\jmath}, \vec{k})$ un repère de l'espace. Soient $A\left(x_{A} ; y_{A} ; z_{A}\right)$ et $B\left(x_{B} ; y_{B} ; z_{B}\right)$ deux points de l'espace.

Le vecteur $\overrightarrow{A B}$ admet pour coordonnées ( $x_{B}-x_{A} ; y_{B}-y_{A} ; z_{B}-z_{A}$ ). Le milieu du segment $[A B]$ admet pour coordonnées $\left(\frac{x_{A}+x_{B}}{2} ; \frac{y_{A}+y_{B}}{2} ; \frac{z_{A}+z_{B}}{2}\right)$.

Propriété

Soient $(O, \vec{\imath}, \vec{\jmath}, \vec{k})$ un repère de l'espace. Soient $\vec{u}(x ; y ; z)$ et $\vec{V}\left(x^{\prime} ; y^{\prime} ; z^{\prime}\right)$ deux vecteurs de l'espace, et soit $k$ un nombre réel. Le vecteur $\vec{u}+\vec{v}$ admet pour coordonnées $\left(x+x^{\prime} ; y+y^{\prime} ; z+z^{\prime}\right)$. Le vecteur $k \vec{u}$ admet pour coordonnées ( $k x, k y$; $k z$ ).