Exercices : Fonction logarithme népérien

Exercices corrigés

Exercice 1

Soit $h$ définie sur $] 0 ;+\infty[\operatorname{par} h(x)=x \ln x+3 x$. Le point $\mathrm{A}(2 \mathrm{e} ; 9 \mathrm{e})$ est-il sur la tangente $t$ à $\mathrm{C}_{h}$ en e ?

Corrigé

Dérivons $h(x)$ On pose $u=x$ et $v=\ln x$. Donc $u^{\prime}=1$ et $v^{\prime}=\frac{1}{x}$. Ici $h=u v+3 x$ et donc $h^{\prime}=u^{\prime} v+u v^{\prime}+3$. Donc $h^{\prime}(x)=1 \times \ln x+x \times \frac{1}{x}+3=\ln x+1+3=\ln x+4$. $h(e)=e \ln e+3 e=e \times 1+3 e=e+3 e=4 e$. $h^{\prime}(e)=\ln e+4=1+4=5$. La tangente à $\mathrm{C}{h}$ en $x{0}$ a pour équation $y=h\left(x_{0}\right)+h^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)$. ici : $x_{0}=e, h\left(x_{0}\right)=4 e, h^{\prime}\left(x_{0}\right)=5$. D'où l'équation : $y=4 e+5(x-e)$, soit : $y=4 e+5 x-5 e$, soit : $y=5 x-e$. Donc finalement, $t$ a pour équation : $y=5 x-e$.

Or $5 x_{A}-e=5 \times 2 e-e=10 e-e=9 e=y_{A}$. Donc A est sur $t$.

Exercice 2

Soit $x$ un nombre réel. Déterminer le signe de $\quad a=-3 \ln \left(x^{2}+1\right)-e^{-5 x}, \quad$ de $b=\ln \frac{1}{e^{x}+2}$.

Corrigé

$x^{2} \geq 0$ (c'est un carré), donc $x^{2}+1>1$, donc $\ln \left(x^{2}+1\right)>0$, et donc $-3 \ln \left(x^{2}+1\right)<0$. De plus, $e^{-5 x}>0$ (c'est une exponentielle), et par là $-e^{-5 x}<0$. Finalement, $a$ est une somme algébrique de deux termes strictement négatifs, et par là : $a<0$. $e^{x}>0$ (c'est une exponentielle), et par là $e^{x}+2>2$.

Donc $\frac{1}{e^{x}+2}<\frac{1}{2}$, et par là $\frac{1}{e^{x}+2}<1$, et donc $\ln \frac{1}{e^{x}+2}<0$, soit $b<0$.

Exercice 3

Écrire $A$ et $B$ sous la forme $a \ln b+c$, où $a, b$ et $c$ sont des réels, avec $b<7$. $A=\ln 225-2 \ln 3+\ln \left(e^{9}\right) \quad B=3 \ln 24 e-\ln 64+e^{\ln 7}$.

Corrigé

$A=\ln 225-2 \ln 3+\ln \left(e^{9}\right)=\ln 15^{2}-2 \ln 3+9$. Soit : $A=2(\ln 15-\ln 3)+9=2 \ln \frac{15}{3}+9=2 \ln 5+9$. $B=3 \ln 24 e-\ln 64+e^{\ln 7}=3(\ln 24+\ln e)-\ln 4^{3}+7$. Soit: $B=3 \ln 24+3 \ln e-3 \ln 4+7$. Soit : $B=3 \ln 24+3 \times 1-3 \ln 4+7=3 \ln \frac{24}{4}+10=3 \ln 6+10$.

Exercice 4

1. Résoudre l'équation $\ln (-3 x+1)=6$.
2. Résoudre l'inéquation $\ln (x+3)+1 \leq 3$.
3. Résoudre l'équation $\ln (x+2)+\ln (x-1)=\ln (2 x+10)$.
4. Résoudre l'équation $\ln (x+2)(x-1)=\ln (2 x+10)$.

Corrigé

1. On doit avoir $-3 x+1>0$, soit $-3 x>-1$, soit $x<\frac{-1}{-3}$, soit $x<\frac{1}{3}$.

Donc $\left.\mathrm{D}_{E}=\right]-\infty ; \frac{1}{3}[$. $\ln (-3 x+1)=6 \Leftrightarrow e^{\ln (-3 x+1)}=e^{6} \Leftrightarrow-3 x+1=e^{6} \Leftrightarrow-3 x=e^{6}-1$

$$ \Leftrightarrow x=\frac{e^{6}-1}{-3}=\frac{1-e^{6}}{3} . $$

Donc $S=\left{\frac{1-e^{6}}{3}\right}$. Notons que $\frac{1-e^{6}}{3} \approx-134$ est bien dans $D_{E}$. 2. On doit avoir $x+3>0$, soit $x>-3$. Donc $\left.\mathrm{D}_{E}=\right]-3 ;+\infty[$.

$$ \begin{aligned} \ln (x+3)+1 \leq 3 & \Leftrightarrow \ln (x+3) \leq 3-1 \Leftrightarrow \ln (x+3) \leq 2 \Leftrightarrow e^{\ln (x+3)} \leq e^{2} \ & \Leftrightarrow x+3 \leq e^{2} \Leftrightarrow x \leq e^{2}-3 \end{aligned} $$

Donc $\mathrm{S}=]-3 ; e^{2}-3\left[\right.$. Notons que $e^{2}-3 \approx 4,39$. 3. On doit avoir $x+2>0$, soit $x>-2$.

On doit avoir $x-1>0$, soit $x>1$. On doit avoir $2 x+10>0$, soit $x>-5$. Donc, finalement : $\left.\mathrm{D}{E}=\right] 1 ;+\infty[$. (E) $\Leftrightarrow \ln (x+2)(x-1)=\ln (2 x+10)$ $\Leftrightarrow(x+2)(x-1)=2 x+10 \Leftrightarrow x^{2}-x-12=0$. C'est un trinôme, de discriminant 49, admettant 2 racines -3 et 4 . La solution -3 est à rejeter car elle n'appartient pas à $\mathrm{D}{E}$. Donc $\mathrm{S}={4}$. 4. On doit avoir $(x+2)(x-1)>0$.

Le membre de gauche est un trinôme $\left(x^{2}+x-2\right)$ de racines -2 et 1 , à coefficient dominant 1 strictement positif. Il est donc strictement positif sur $]-\infty$; -2 [ d'une part, et sur ] $1 ;+\infty$ [ d'autre part. Par ailleurs, on doit aussi avoir $2 x+10>0$, soit $x>-5$. Donc, finalement : $\left.\mathrm{D}_{E}=\right]-5 ;-2[\cup] 1 ;+\infty[$. (E) $\Leftrightarrow(x+2)(x-1)=2 x+10 \Leftrightarrow x^{2}-x-12=0$.

C'est un trinôme, de discriminant 49, admettant 2 racines -3 et 4 . Ces 2 valeurs appartiennent à $\mathrm{D}_{E}$. Donc $\mathrm{S}={-3 ; 4}$. Comparer cette question à la précédente; cela fait réfléchir !

Exercice 5

Soit $f$ définie sur $\left[\frac{1}{e} ; e\right] \operatorname{par} f(x)=x^{2}+x-3 \ln x$.

1. Déterminer $f^{\prime}(x)$, étudier son signe, et dresser le tableau de variation de $f$ sur $\left[\frac{1}{e} ; e\right]$.
2. Montrer que l'équation $f(x)=4$ admet une solution unique $s$ sur l'intervalle [ $1 ; e$ ].
3. Recopier l'algorithme suivant, et compléter les 2 lignes incomplètes pour que, à la fin de son exécution, les variables A et B fournissent un encadrement d'amplitude 0,01 de la solution $s$. $A \leftarrow 1$ $B \leftarrow e$ $L \leftarrow 4$ $D \leftarrow 0,01$

Tant que ...

Si $f\left(\frac{A+B}{2}\right) \ldots$ Alors $B \leftarrow \frac{A+B}{2}$ Sinon $A \leftarrow \frac{A+B}{2}$ Fin du $\mathbf{S i}$ Fin du Tant que

Corrigé

1. Dérivons $f(x)$

Donc $f^{\prime}(x)=2 x+1-3 \frac{1}{x}=\frac{2 x^{2}}{x}+\frac{x}{x}-\frac{3}{x}=\frac{2 x^{2}+x-3}{x}$.

Le numérateur est un trinôme avec $a=2, b=1$ et $c=-3$. $\Delta=b^{2}-4 a c=1^{2}-4 \times 2 \times(-3)=1+24=25$. $\Delta>0$. Le trinôme a 2 racines. $x_{1}=\frac{-b-\sqrt{\Delta}}{2 a}=\frac{-1-5}{4}=-1,5$ (hors intervalle) $\quad$ et $x_{2}=\frac{-b+\sqrt{\Delta}}{2 a}=\frac{-1+5}{4}=1$. Le trinôme est du signe de $a$ (positif) à l'extérieur des racines.

Le dénominateur est strictement positif sur $\mathbb{R}+$, et donc sur $\left[\frac{1}{e} ; e\right]$.

D'où le tableau de signes de $f^{\prime}$ et de variation de $f$.

$x$	$1 / e$		1	$e$
$f^{\prime}(x)$		-	0	+
	$f(1 / e)$
$f(x)$

On note que : $f(1)=1^{2}+1-3 \ln 1=1+1-3 \times 0=2$.

$$ \begin{aligned} f\left(\frac{1}{e}\right) & =\left(\frac{1}{e}\right)^{2}+\frac{1}{e}-3 \ln \frac{1}{e}=\frac{1}{e^{2}}+\frac{1}{e}-3(\ln 1-\ln e) \ & =\frac{1}{e^{2}}+\frac{1}{e}-3(0-1)=\frac{1}{e^{2}}+\frac{1}{e}+3 \approx 3,5 \end{aligned} $$

$f(e)=e^{2}+e-3 \ln e=e^{2}+e-3 \times 1=e^{2}+e-3 \approx 7,1$. 2. D'après le tableau de variation, la fonction $f$ est continue et strictement croissante sur $[1 ; e]$. Or 4 est un nombre compris entre $f(1)=2$ et $f(e) \approx 7,1$,

Donc, d'après le théorème de la bijection, l'équation $f(x)=4$ admet une unique solution sur $[1 ; e]$. 3. Algorithme complet : $A \leftarrow 1$ $B \leftarrow e$ $L \leftarrow 4$ $D \leftarrow 0,01$ Tant que $B-A>D$ Si $f\left(\frac{A+B}{2}\right)>L$ Alors $B \leftarrow \frac{A+B}{2}$ Sinon $A \leftarrow \frac{A+B}{2}$ Fin du $\mathbf{S i}$ Fin du Tant que

Exercice 6

Soit C la courbe représentative de $f(x)=3 \ln \left(x^{2}+1\right)-x^{3}+3,6 x+0,8$.

Déterminer une équation de $d$, tangente à $C$ en 2 . Présenter cette équation sous la forme $y=a x+\ln b$, où $a$ est un réel quelconque, et $b$ un réel strictement positif.

Corrigé

On a $f^{\prime}(x)=3 \frac{2 x}{x^{2}+1}-3 x^{2}+3,6$. $d$ a pour équation $y=f\left(x_{0}\right)+f^{\prime}\left(x_{0}\right)\left(x-x_{0}\right)$. ici : $x_{0}=2$, $f\left(x_{0}\right)=3 \ln \left(2^{2}+1\right)-2^{3}+3,6 \times 2+0,8=3 \ln 5-8+7,2+0,8=3 \ln 5$. $f^{\prime}\left(x_{0}\right)=3 \frac{2 \times 2}{2^{2}+1}-3 \times 2^{2}+3,6=2,4-12+3,6=-6$. D'où l'équation de $d: y=3 \ln 5-6(x-2)$. Soit : $y=3 \ln 5-6 x+12$, soit : $y=-6 x+3 \ln 5+12$. Soit : $y=-6 x+\ln 5^{3}+12 \ln e$, soit : $y=-6 x+\ln 125+\ln e^{12}$. Soit : $y=-6 x+\ln \left(125 e^{12}\right)$. L'équation de la tangente $d$ est bien sous la forme demandée avec $a=-6$ et $b=125 e^{12}$.

Exercice 7

Dans chacun des cas suivants, dire si la suite ( $u_{n}$ ) est géométrique ou arithmétique. Justifier. Donner la raison de la suite.

1. $\forall n \in \mathrm{~N}, \ln u_{n+1}=\ln 10+\ln u_{n}$
2. $\forall n \in \mathrm{~N}, u_{n}=8,1 e^{-n \ln 3}$
3. $\forall n \in \mathrm{~N}, e^{u_{n+1}}=2 e^{u_{n}}$
4. $\forall n \in \mathrm{~N}, u_{n}=\ln \left(3,2 e^{2,5 n}\right)$

Corrigé

1. Soit $n \in \mathrm{~N}$, $\ln u_{n+1}=\ln 10+\ln u_{n} \Leftrightarrow \ln u_{n+1}=\ln \left(10 \times u_{n}\right) \Leftrightarrow u_{n+1}=10 \times u_{n}$. Donc: $\forall n \in \mathrm{~N}, u_{n+1}=10 u_{n}$. Donc la suite ( $u_{n}$ ) est géométrique de raison 10 .
2. Soit $n \in \mathrm{~N}$, $u_{n}=8,1 e^{-n \ln 3}=8,1\left(e^{\ln 3}\right)^{-n}=8,1 \times 3^{-n}=8,1 \frac{1}{3^{n}}=8,1\left(\frac{1}{3}\right)^{n}$. Donc: $\forall n \in \mathrm{~N}, u_{n}=8,1\left(\frac{1}{3}\right)^{n}$. Donc la suite $\left(u_{n}\right)$ est géométrique de raison $\frac{1}{3}$.
3. Soit $n \in \mathrm{~N}, e^{u_{n+1}}=2 e^{u_{n}} \Leftrightarrow e^{u_{n+1}}=e^{\ln 2} e^{u_{n}} \Leftrightarrow e^{u_{n+1}}=e^{\ln 2+u_{n}}$.

Donc: $\forall n \in \mathrm{~N}, u_{n+1}=u_{n}+\ln 2$. Donc la suite ( $u_{n}$ ) est arithmétique de raison $\ln 2$. 4. Soit $n \in \mathrm{~N}, u_{n}=\ln \left(3,2 e^{2,5 n}\right)=\ln 3,2+\ln \left(e^{2,5 n}\right)=\ln 3,2+2,5 n$.

Donc $\forall n \in \mathrm{~N}, u_{n}=2,5 n+\ln 3,2$. Donc la suite ( $u_{n}$ ) est arithmétique de raison 2,5.

Exercice 8

Cet exercice utilise primitives et intégrales. Soit $f$ définie sur $[1,4]$ par $f(x)=5 \ln x-2$, représentée par C .

1. Déterminer $f^{\prime}$, puis le signe de $f^{\prime}$, et dresser le tableau de variation de $f$ sur $[1,4]$.
2. Montrer que $f$ est strictement positive sur $[2 ; 4]$.
3. Pourquoi $f$ est-elle continue sur $[2 ; 4]$ ?
4. Tracer rapidement $C$ sur $[1 ; 4]$.
5. Montrer que $x \ln x-x$ est une primitive de $\ln x$ sur $] 0 ;+\infty[$.
6. En déduire une primitive $F$ de la fonction $f$ sur $[2,4]$.
7. Soit $A$ l'aire du domaine situé entre $C$, l'axe des abscisses, les droites d'équation $x=2$ et $x=4$. Montrer que $A=30 \ln 2-14$.
8. Calculer $m$, valeur moyenne de $f$ entre 2 et 4 . Interpréter graphiquement.

Corrigé

1. $f^{\prime}(x)=5 \frac{1}{x}-0=\frac{5}{x}$.

Or, $\frac{5}{x}$ est strictement positif pour $x$ strictement positif. Donc $f^{\prime}$ est strictement positive sur $[1,4]$. D'où le tableau de variation de $f$.

$x$	1		4
$f^{\prime}(x)$		+
$f(x)$

2. Soit $x$ dans l'intervalle [2;4]. Donc on a, en particulier $2<x$.

Comme $f$ est strictement croissante, on obtient : $f(2)<f(x)$. Or, $f(2) \approx 1,4$ est strictement positif. Donc, on obtient : $0<f(x)$. Donc $f$ est strictement positive sur [2;4]. 3. $f$, dérivable sur $[2 ; 4]$, y est donc continue. 4. Valeurs à 0,001 près

$x$	1	2	3	4
$f(x)$	-2	1,466	3,493	4,931

Tracé de C 5. Posons $G(x)=x \ln x-x$ et $g(x)=\ln x$. Dérivons $G$.

On pose : $G=u v-x$ avec $u=x, v=\ln x, u^{\prime}=1, v^{\prime}=\frac{1}{x}$. On a: $G^{\prime}=u^{\prime} v+u v^{\prime}-1$. Soit : $G^{\prime}(x)=1 \times \ln x+x \times \frac{1}{x}-1=\ln x+1-1=\ln x=g(x)$. Donc $G^{\prime}=g$ sur $] 0 ;+\infty[$. Et donc $x \ln x-x$ est une primitive de $\ln x$ sur $] 0 ;+\infty[$. 6. $f=5 g-2$; donc, par exemple : $F=5 G-2 x$ est une primitive de $f$.

Soit $F(x)=5(x \ln x-x)-2 x=5 x \ln x-7 x$. 7. Comme $f$ est continue et positive sur [2; 4], on a : $A=\int_{2}^{4} f(x) d x$.

Soit : $A=F(4)-F(2)=(20 \ln 4-28)-(10 \ln 2-14)$. Soit : $A=20 \ln 2^{2}-28-10 \ln 2+14$. Soit : $A=40 \ln 2-10 \ln 2-14=30 \ln 2-14$. 8. $\quad m=\frac{1}{4-2} \int_{2}^{4} f(x) d x=\frac{1}{2}(30 \ln 2-14)=15 \ln 2-7 \approx 3,4$.

C'est aussi l'aire du rectangle de côtés 2 et $m$.

Exercice 9

Cet exercice utilise primitives et intégrales. Soit $f$ définie sur $\left[1,+\infty\left[\operatorname{par} f(x)=\frac{1}{x+1}+\ln \frac{x}{x+1}\right.\right.$, représentée par C .

1. Déterminer $\lim _{x \rightarrow+\infty} f(x)$.
2. Montrer que, pour tout $x$ de $\left[1,+\infty\left[, f^{\prime}(x)=\frac{1}{x(x+1)^{2}}\right.\right.$.
3. En déduire le signe de la fonction $f$ sur $[1,+\infty[$.
4. Soit ( $u_{n}$ ) la suite définie, pour tout entier naturel $n$ non nul, par : $u_{n}=1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{n}-\ln n$. Démontrer que, pour tout entier naturel $n$ non nul, $u_{n+1}-u_{n}=f(n)$. En déduire le sens de variation de la suite $\left(u_{n}\right)$.
5. Soit $k$ un entier strictement positif.

Montrer que : $\int_{k}^{k+1}\left(\frac{1}{k}-\frac{1}{x}\right) d x \geq 0$. Montrer que : $\int_{k}^{k+1}\left(\frac{1}{k}-\frac{1}{x}\right) d x \geq 0$. En déduire que : $\int_{k}^{k+1} \frac{1}{x} d x \leq \frac{1}{k}$. Montrer que : $\ln (k+1)-\ln k \leq \frac{1}{k}$ 6. Écrire l'inégalité (E) en remplaçant successivement $k$ par $1,2, \ldots, n$ et démontrer que: pour tout entier naturel $n$ non nul, $\ln (n+1) \leq 1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{n}$. 7. En déduire que, pour tout entier naturel $n$ non nul, $u_{n}>0$. 8. Prouver que la suite $\left(u_{n}\right)$ est convergente.

Corrigé

1. Pour commencer, comme $\lim _{x \rightarrow+\infty} x+1=+\infty$, on obtient : $\lim _{x \rightarrow+\infty} \frac{1}{x+1}=0$.

Regardons le second terme; on a : $\frac{x}{x+1}=\frac{x}{x\left(1+\frac{1}{x}\right)}=\frac{1}{1+\frac{1}{x}}$. Donc : $\lim _{x \rightarrow+\infty} \frac{x}{x+1}=\frac{1}{1+0}=1$. Or: $\lim _{y \rightarrow 1} \ln y=\ln 1=0$. Par conséquent : $\lim _{x \rightarrow+\infty} \ln \frac{x}{x+1}=0$ (limite d'une composée). Donc, finalement : $\lim _{x \rightarrow+\infty} f(x)=0+0=0$ (limite d'une somme). 2. On pose: $f=\frac{1}{u}+\ln w$, avec $u=x+1$ et $w=\frac{x}{x+1}$.

On a donc : $f^{\prime}=\frac{-u^{\prime}}{u^{2}}+\frac{w^{\prime}}{w}$, avec $u^{\prime}=1$ et $w^{\prime}$ à déterminer. On a : $w^{\prime}=\frac{1 \times(x+1)-x \times 1}{(x+1)^{2}}=\frac{x+1-x}{(x+1)^{2}}=\frac{1}{(x+1)^{2}}$. Donc, finalement : $f^{\prime}(x)=\frac{-1}{(x+1)^{2}}+\frac{\frac{1}{(x+1)^{2}}}{\frac{x}{x+1}}=\frac{-1}{(x+1)^{2}}+\frac{1}{(x+1)^{2}} \frac{x+1}{x}$. Soit : $f^{\prime}(x)=\frac{-1}{(x+1)^{2}}+\frac{1}{x(x+1)}=\frac{-x}{x(x+1)^{2}}+\frac{x+1}{x(x+1)^{2}}=\frac{-x+x+1}{x(x+1)^{2}}=\frac{1}{x(x+1)^{2}}$. 3. Sur $[1,+\infty[, x$ est strictement positif.

Et le carré $(x+1)^{2}$ est strictement positif (il s'annulerait en -1 ). Donc $f^{\prime}(x)$ est strictement positif sur $[1,+\infty[$. Et par là, $f$ est strictement croissante sur $[1,+\infty[$. Et comme $\lim _{x \rightarrow+\infty} f(x)=0$, on en déduit que $f$ reste strictement négative sur $[1,+\infty[$. 4. Soit $n$ un entier naturel non nul.

On a: $u_{n+1}-u_{n}=1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{n}+\frac{1}{n+1}-\ln (n+1)$

$$ -\left(1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{n}-\ln n\right) . $$

Soit : $u_{n+1}-u_{n}=1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{n}+\frac{1}{n+1}-\ln (n+1)$

$$ -1-\frac{1}{2}-\frac{1}{3}-\ldots-\frac{1}{n}+\ln n $$

Soit : $u_{n+1}-u_{n}=\frac{1}{n+1}-\ln (n+1)+\ln n=\frac{1}{n+1}+\ln \frac{n}{n+1}=f(n)$. Donc, pour tout $n$ entier naturel non nul, on a : $u_{n+1}-u_{n}=f(n)$. Or on a vu que $f$ est strictement négative. Donc, pour tout $n$ entier naturel non nul, $u_{n+1}<u_{n}$, et par là, la suite ( $u_{n}$ ) est strictement décroissante. 5. Soit $k$ un entier strictement positif.

Soit $x$ dans l'intervalle $[k ; k+1]$. Notons ici que $x$ et $k$ sont strictement positifs. De plus : $x \geq k$. On note alors que, comme $x$ et $k$ sont strictement positifs, le passage aux inverses inverse le sens de l'inégalité. D'où : $\frac{1}{x} \leq \frac{1}{k}$, et par là : $\frac{1}{k}-\frac{1}{x} \geq 0$.

Par positivité de l'intégrale, on obtient: $\int_{k}^{k+1}\left(\frac{1}{k}-\frac{1}{x}\right) d x \geq 0$. D'où, par linéarité : $\int_{k}^{k+1} \frac{1}{k} d x-\int_{k}^{k+1} \frac{1}{x} d x \geq 0$. Et donc : $\int_{k}^{k+1} \frac{1}{k} d x \geq \int_{k}^{k+1} \frac{1}{x} d x$. Or : $\int_{k}^{k+1} \frac{1}{x} d x=[\ln x]{k}^{k+1}=\ln (k+1)-\ln k$. Et : $\quad \int{k}^{k+1} \frac{1}{k} d x=\left[\frac{1}{k} x\right]_{k}^{k+1}=\frac{1}{k}(k+1)-\frac{1}{k} k=\frac{1}{k}$. Par conséquent : $\frac{1}{k} \geq \ln (k+1)-\ln k$. 6. On écrit les $n$ inégalités suivantes :

$$ \begin{aligned} & 1 \geq \ln (2)-\ln 1 \ & \frac{1}{2} \geq \ln (3)-\ln 2 \ & \cdots \ & \frac{1}{n-1} \geq \ln n-\ln (n-1) \ & \frac{1}{n} \geq \ln (n+1)-\ln n \end{aligned} $$

En sommant membre à membre ces $n$ inégalités, on obtient: $1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{n} \geq \ln (n+1)-\ln 1$, soit : $1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{n} \geq \ln (n+1)$ 7. On déduit de l'inégalité précédente que : $1+\frac{1}{2}+\frac{1}{3}+\ldots+\frac{1}{n}-\ln n \geq \ln (n+1)-\ln n$. Soit: $u_{n} \geq \ln (n+1)-\ln n$. Et comme ln est strictement croissante, on a: $\ln (n+1)-\ln n>0$. Et par là, pour tout entier naturel $n$ non nul, $u_{n}>0$. 8. La suite ( $u_{n}$ ) est décroissante (d'après le 4.) et minorée par 0 (d'après le 7.).

Par conséquent, la suite $\left(u_{n}\right)$ est convergente.

Exercice 10

Cet exercice, assez technique, utilise limites, primitives et intégrales. Soit $f$ définie sur $] 0,+\infty\left[\operatorname{par} f(t)=\frac{1}{t(t+1)^{2}}\right.$. La fonction $f$ est représentée par la courbe C ci-dessous.

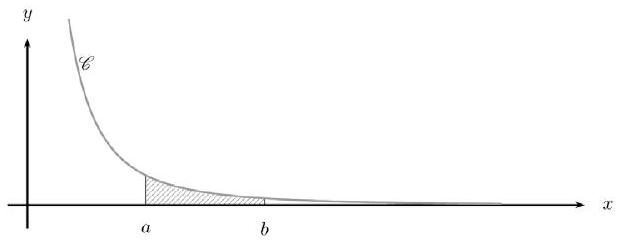
1. Étudier le sens de variation de $f$ et sa limite en $+\infty$.
2. Montrer que, pour tout $t$ de $] 0,+\infty\left[\right.$, on a : $f(t)=-\frac{1}{(t+1)^{2}}-\frac{1}{(t+1)}+\frac{1}{t}$.
3. Dans tout ce qui suit, $a$ et $b$ sont deux réels de $] 0,+\infty[$ tels que $a<b$.

Démontrer l'existence du réel $\quad A(a, b)=\int_{a}^{b} f(t) d t$. Donner une interprétation géométrique de ce réel. Montrer que : $A(a, b)=\frac{1}{1+b}-\frac{1}{1+a}-\ln \frac{1+b}{1+a}+\ln \frac{b}{a}$. 4. Soit $g$ définie sur $] 0,+\infty\left[\operatorname{par} g(t)=-\frac{1}{t^{2}(t+1)}\right.$.

On admet que, pour tout $t$ de $] 0,+\infty\left[\right.$, on a : $g(t)-f(t)=-\frac{1+2 t}{\left(t+t^{2}\right)^{2}}$. Montrer que: $\quad \int_{a}^{b} g(t)-f(t) d t=\frac{1}{b+b^{2}}-\frac{1}{a+a^{2}}$. 5. On pose : $\quad B(a, b)=\int_{a}^{b} g(t) d t \quad$.

À l'aide des résultats obtenus précédemment, montrer que : $B(a, b)=\frac{1}{b+b^{2}}-\frac{1}{a+a^{2}}+\frac{1}{1+b}-\frac{1}{1+a}-\ln \frac{1+b}{1+a}+\ln \frac{b}{a}$. 6. Le réel $a$ est supposé fixé. Déterminer $\lim _{b \rightarrow+\infty} A(a, b)$.

On appellera $F(a)$ la limite trouvée. 7. Le réel $a$ est supposé fixé. Déterminer $\lim _{b \rightarrow+\infty} B(a, b)$.

On appellera $G(a)$ la limite trouvée. 8. On admettra que, pour tout $t$ de $] 0,+\infty\left[\right.$, on a : $F(t)=-\frac{1}{t+1}+\ln \left(1+\frac{1}{t}\right)$.

Montrer que F est strictement décroissante et que $\lim _{t \rightarrow+\infty} F(t)=0$. En déduire le signe de $F$ sur $] 0,+\infty[$. 9. On admettra que $G$ est strictement négative sur $] 0,+\infty[$.

Montrer que, pour tout $t$ de $] 0,+\infty\left[\right.$, on a : $\left(1+\frac{1}{t}\right)^{t}<e<\left(1+\frac{1}{t}\right)^{t+1}$. 10. Montrer que, quel que soit l'entier naturel non nul $n$, on a : $1<\frac{e}{\left(1+\frac{1}{n}\right)^{n}}<1+\frac{1}{n}$. Puis en déduire que : $\lim _{n \rightarrow+\infty}\left(1+\frac{1}{n}\right)^{n}=e$.

Corrigé

1. $f^{\prime}(t)=-\frac{(t+1)^{2}+2 t(t+1)}{t^{2}(t+1)^{2}}=-\frac{(3 t+1)(t+1)}{t^{2}(t+1)^{2}}$.

Il est clair que, sur $] 0,+\infty\left[\right.$, on a : $3 t+1>0, t+1>0, t^{2}>0$ et $(t+1)^{2}>0$. Par conséquent, $f^{\prime}(t)<0$ sur $] 0,+\infty[$, et par là, $f$ y est strictement décroissante. On a : $\lim _{t \rightarrow+\infty} t=+\infty$ et $\lim _{t \rightarrow+\infty}(t+1)^{2}=+\infty$. Donc : $\lim _{t \rightarrow+\infty} t(t+1)^{2}=+\infty$. Et par là : $\lim _{t \rightarrow+\infty} f(t)=0$. 2. Soit $t$ dans $] 0,+\infty[$.

On a : $-\frac{1}{(t+1)^{2}}-\frac{1}{(t+1)}+\frac{1}{t}=-\frac{t}{t(t+1)^{2}}-\frac{t(t+1)}{t(t+1)^{2}}+\frac{(t+1)^{2}}{t(t+1)^{2}}$. Soit : $-\frac{1}{(t+1)^{2}}-\frac{1}{(t+1)}+\frac{1}{t}=\frac{-t-t(t+1)+(t+1)^{2}}{t(t+1)^{2}}$. Soit : $-\frac{1}{(t+1)^{2}}-\frac{1}{(t+1)}+\frac{1}{t}=\frac{\left.-t-t^{2}-t+t^{2}+2 t+1\right)^{2}}{t(t+1)^{2}}$. Soit : $-\frac{1}{(t+1)^{2}}-\frac{1}{(t+1)}+\frac{1}{t}=\frac{1)^{2}}{t(t+1)^{2}}=f(t)$.

L'égalité est évidemment vérifiée pour tout $t \mathrm{de}] 0,+\infty[$. c.q.f.d. 3. $a$ et $b$ sont deux réels de $] 0,+\infty[$ tels que $a<b$.

De plus, $f$, dérivable sur $] 0,+\infty[$, y est donc continue. Enfin, $f$ est clairement positive sur $] 0,+\infty[$. Donc le réel $\quad A(a, b)=\int_{a}^{b} f(t) d t \quad$ existe, et représente l'aire (en unités d'aires) du domaine situé entre C , l'axe des abscisses, et les droites d'équation $x=a$ et $x=b$. Le domaine en question est hachuré sur le dessin. On calcule : $A(a, b)=\left[\frac{1}{1+t}-\ln (1+t)+\ln t\right]{a}^{b}$ Soit : $A(a, b)=\frac{1}{1+b}-\frac{1}{1+a}-(\ln (1+b)-\ln (1+a))+\ln b-\ln a$ Soit : $A(a, b)=\frac{1}{1+b}-\frac{1}{1+a}-\ln \frac{1+b}{1+a}+\ln \frac{b}{a} \quad$ c.q.f.d. 4. On a : $g(t)-f(t)=-\frac{1+2 t}{\left(t+t^{2}\right)^{2}}=-v^{\prime} v^{2} \quad$ avec $v=t+t^{2}$ et $v^{\prime}=1+2 t$. Donc une primitive de $g(t)-f(t)$ est $\frac{1}{v}=\frac{1}{t+t^{2}}$. Donc : $\int{a}^{b} g(t)-f(t) d t=\left[\frac{1}{t+t^{2}}\right]_{a}^{b}=\frac{1}{b+b^{2}}-\frac{1}{a+a^{2}} \quad$ c.q.f.d. 5. Nous utilisons la linéarité de l'intégrale.

On a : $\quad B(a, b)=\int_{a}^{b} g(t) d t=\int_{a}^{b} g(t)-f(t) d t+\int_{a}^{b} f(t) d t \quad$. Soit :

$$ B(a, b)=\int_{a}^{b} g(t) d t=\frac{1}{b+b^{2}}-\frac{1}{a+a^{2}}+\frac{1}{1+b}-\frac{1}{1+a}-\ln \frac{1+b}{1+a}+\ln \frac{b}{a} $$

c.q.f.d.

6. Le réel $a$, strictement positif, est supposé fixé.

On a: $\lim _{b \rightarrow+\infty} \frac{1}{1+b}-\frac{1}{1+a}=0-\frac{1}{1+a}=-\frac{1}{1+a}$. Notons ici que, si l'on cherche directement la limite des autres termes, alors on tombe sur une forme indéterminée.

En effet, on a: $\lim _{b \rightarrow+\infty} 1+b=+\infty$, et comme $1+a>0$, on a : $\lim _{b \rightarrow+\infty} \frac{1+b}{1+a}=+\infty$. Or: $\lim _{Y \rightarrow+\infty}-\ln Y=-\infty$. Donc : $\lim _{b \rightarrow+\infty}-\ln \frac{1+b}{1+a}=-\infty$. Et, pour une raison similaire, on a : $\lim _{b \rightarrow+\infty} \ln \frac{b}{a}=+\infty$. On constate que l'on a alors une forme indéterminée ! On regroupe alors les 2 termes posant problème. On a $:-\ln \frac{1+b}{1+a}+\ln \frac{b}{a}=\ln \frac{b(1+a)}{a(1+b)}=\ln \frac{b(1+a)}{a b\left(\frac{1}{b}+1\right)}=\ln \frac{1+a}{a\left(\frac{1}{b}+1\right)}$. Or: $\lim _{b \rightarrow+\infty} \ln \frac{1+a}{a\left(\frac{1}{b}+1\right)}=\ln \frac{1+a}{a(0+1)}=\ln \frac{1+a}{a}$. Donc finalement : $\lim _{b \rightarrow+\infty} A(a, b)=-\frac{1}{1+a}+\ln \frac{1+a}{a}$. On a donc: $F(a)=-\frac{1}{1+a}+\ln \left(1+\frac{1}{a}\right)$. Pour information, $F(a)$ est l'aire du domaine situé entre C , l'axe des abscisses, et la droite d'équation $x=a$. Ce domaine «infini» a une aire finie. 7. Comme précédemment, on obtient : $\lim _{b \rightarrow+\infty} B(a, b)=-\frac{1}{a+a^{2}}-\frac{1}{1+a}+\ln \frac{1+a}{a}$.

Soit : $G(a)=-\frac{1}{a(1+a)}-\frac{a}{a(1+a)}+\ln \left(\frac{1}{a}+1\right)$. On a donc : $G(a)=-\frac{1}{a}+\ln \left(1+\frac{1}{a}\right)$. 8. On a: $F(t)=-\frac{1}{t+1}+\ln \left(1+\frac{1}{t}\right)$.

Donc : $F^{\prime}(t)=-\frac{-1}{(t+1)^{2}}+\frac{\frac{-1}{t^{2}}}{1+\frac{1}{t}}=\frac{1}{(t+1)^{2}}-\frac{t}{t^{2}(t+1)}$. Soit : $F^{\prime}(t)=\frac{1}{(t+1)^{2}}-\frac{1}{t(t+1)}=-\frac{1}{t(t+1)^{2}}=-f(t)$. Or on a vu que $f(t)>0$ sur $] 0,+\infty[$. Par conséquent, $F^{\prime}(t)<0$ sur $] 0,+\infty[$, et par là, $F$ y est strictement décroissante.

On a : $\lim _{t \rightarrow+\infty} 1+t=+\infty$, et donc $\lim _{t \rightarrow+\infty} \frac{1}{1+t}=0$. Par ailleurs : $\lim _{t \rightarrow+\infty} \ln \left(1+\frac{1}{t}\right)=\ln (1+0)=\ln 1=0$. Et par là : $\lim _{t \rightarrow+\infty} F(t)=0$.

Finalement, $F$ est strictement décroissante sur $] 0,+\infty\left[\right.$ et $\lim _{t \rightarrow+\infty} F(t)=0$. Par conséquent, $F$ est strictement positive sur $] 0,+\infty[$. Tout cela est cohérent avec la remarque du 6. La fonction $F$ est bien positive car elle représente l'aire d'un domaine. Notons de plus que, quandt tend vers $+\infty, F$ décroît car le domaine rétrécit. Mais le fait que la limite vaille 0 n'est pas intuitivement évident, car, comme chacun sait, une fonction peut être décroissante et tendre vers une valeur strictement positive (par exemple $1+\frac{1}{t}$ ). 9. On admettra que $G$ est strictement négative sur $] 0,+\infty[$.

Soit $t$ dans $] 0,+\infty[$. On a alors : $G(t)<0<F(t)$. Donc : $-\frac{1}{t}+\ln \left(1+\frac{1}{t}\right)<0 \quad$ et $\quad 0<-\frac{1}{t+1}+\ln \left(1+\frac{1}{t}\right)$. Donc: $\ln \left(1+\frac{1}{t}\right)<\frac{1}{t} \quad$ et $\quad \frac{1}{t+1}<\ln \left(1+\frac{1}{t}\right)$. Et comme $t$ et $t+1$ sont strictement positifs, on obtient: $t \ln \left(1+\frac{1}{t}\right)<1 \quad$ et $\quad 1<(t+1) \ln \left(1+\frac{1}{t}\right)$. Soit : $\ln \left(1+\frac{1}{t}\right)^{t}<\ln e<\ln \left(1+\frac{1}{t}\right)^{(t+1)}$. On rappelle ici que $e^{\ln a}=$ a pour $a>0$. Par stricte croissance de la fonction exponentielle, on obtient alors finalement : $\left(1+\frac{1}{t}\right)^{t}<e<\left(1+\frac{1}{t}\right)^{t+1} \quad$ c.q.f.d. 10. Soit $n$ un entier naturel non nul.

Il est donc positif, et les inégalités précédentes s'appliquent. Elles donnent : $\left(1+\frac{1}{n}\right)^{n}<e<\left(1+\frac{1}{n}\right)^{n+1}$. Et, comme $\left(1+\frac{1}{n}\right)^{n}>0$, on obtient : $1<\frac{e}{\left(1+\frac{1}{n}\right)^{n}}<1+\frac{1}{n}$. Or : $\lim _{t \rightarrow+\infty} 1=1$ et $\lim _{t \rightarrow+\infty} 1+\frac{1}{n}=1+0=1$. Donc, par application du théorème des gendarmes, on obtient: $\lim _{t \rightarrow+\infty} \frac{e}{\left(1+\frac{1}{n}\right)^{n}}=1$. Et, par conséquent : $\lim _{n \rightarrow+\infty}\left(1+\frac{1}{n}\right)^{n}=e$ c.q.f.d.