Exercices : Orthogonalité et distances dans l'espace

Exercices corrigés

Exercice 1

Soit ABCD un tétraèdre tel que l'arête ( AB ) est orthogonale au plan ( BCD ). K est l'orthocentre du triangle BCD . H est le projeté orthogonal de K sur le plan (ACD). Attention! La perspective masque les angles droits... 1.a. Expliquer pourquoi on a : $\overrightarrow{A B} \cdot \overrightarrow{C D}=0$. 1.b. Expliquer pourquoi on a: $\overrightarrow{B K} \cdot \overrightarrow{C D}=0$. 1.c. Expliquer pourquoi on a : $\overrightarrow{K H} \cdot \overrightarrow{C D}=0$. 1.d. Montrer que $: \overrightarrow{A H} \cdot \overrightarrow{C D}=0$. 2.a. Expliquer pourquoi on a: $\overrightarrow{D K} \cdot \overrightarrow{A B}=0$. 2.b. Expliquer pourquoi on a : $\overrightarrow{D K} \cdot \overrightarrow{B C}=0$. 2.c. Expliquer pourquoi on a $: \overrightarrow{K H} \cdot \overrightarrow{A C}=0$. 2.d. Montrer que $: \overrightarrow{D H} \cdot \overrightarrow{A C}=0$. 3. Montrer que $H$ est l'orthocentre du triangle $A C D$.

Corrigé

1.a. $(\mathrm{AB})$ est orthogonale au plan $(\mathrm{BCD})$, donc $\overrightarrow{A B}$ est orthogonal à tout vecteur appartenant à la direction du plan (BCD). En particulier, $\overrightarrow{A B}$ est orthogonal à $\overrightarrow{C D}$. Donc on a : $\overrightarrow{A B} \cdot \overrightarrow{C D}=0$. 1.b. K est l'orthocentre du triangle BCD .

Il est donc à l'intersection des hauteurs de ce triangle. En particulier, K est sur la hauteur de BCD issue de B . Donc $\overrightarrow{B K}$ est orthogonal à $\overrightarrow{C D}$. Donc on a $: \overrightarrow{B K} \cdot \overrightarrow{C D}=0$. 1.c. H est le projeté orthogonal de K sur le plan ( ACD ).

Donc $\overrightarrow{K H}$ est orthogonal à tout vecteur appartenant à la direction du plan (ACD). En particulier, $\overrightarrow{K H}$ est orthogonal à $\overrightarrow{C D}$. Donc on a $: \overrightarrow{K H} \cdot \overrightarrow{C D}=0$. 1.d. On utilise la relation de Chasles.

On obtient $: \overrightarrow{A H} \cdot \overrightarrow{C D}=(\overrightarrow{A B}+\overrightarrow{B K}+\overrightarrow{K H}) \cdot \overrightarrow{C D}$. Soit : $\overrightarrow{A H} \cdot \overrightarrow{C D}=\overrightarrow{A B} \cdot \overrightarrow{C D}+\overrightarrow{B K} \cdot \overrightarrow{C D}+\overrightarrow{K H} \cdot \overrightarrow{C D}$. Et d'après les résultats précédents : $\overrightarrow{A H} \cdot \overrightarrow{C D}=0+0+0=0$. 2.a. $(\mathrm{AB})$ est orthogonale au plan $(\mathrm{BCD})$, donc $\overrightarrow{A B}$ est orthogonal à tout vecteur appartenant à la direction du plan (BCD). En particulier, $\overrightarrow{A B}$ est orthogonal à $\overrightarrow{D K}$. Donc on a $: \overrightarrow{D K} \cdot \overrightarrow{A B}=0$. 2.b. K est l'orthocentre du triangle BCD .

Il est donc à l'intersection des hauteurs de ce triangle. En particulier, K est sur la hauteur de BCD issue de D . Donc $\overrightarrow{D K}$ est orthogonal à $\overrightarrow{B C}$. Donc on a $: \overrightarrow{D K} \cdot \overrightarrow{B C}=0$. 2.c. H est le projeté orthogonal de K sur le plan ( ACD ).

Donc $\overrightarrow{K H}$ est orthogonal à tout vecteur appartenant à la direction du plan (ACD). En particulier, $\overrightarrow{K H}$ est orthogonal à $\overrightarrow{A C}$.

Donc on a $: \overrightarrow{K H} \cdot \overrightarrow{A C}=0$. 2.d. On utilise la relation de Chasles.

On obtient : $\overrightarrow{D H} \cdot \overrightarrow{A C}=(\overrightarrow{D K}+\overrightarrow{K H}) \cdot \overrightarrow{A C}$. Soit $: \overrightarrow{D H} \cdot \overrightarrow{A C}=\overrightarrow{D K} \cdot \overrightarrow{A C}+\overrightarrow{K H} \cdot \overrightarrow{A C}$. On utilise à nouveau la relation de Chasles. On obtient : $\overrightarrow{D H} \cdot \overrightarrow{A C}=\overrightarrow{D K} \cdot(\overrightarrow{A B}+\overrightarrow{B C})+\overrightarrow{K H} \cdot \overrightarrow{A C}$. Soit $: \overrightarrow{D H} \cdot \overrightarrow{A C}=\overrightarrow{D K} \cdot \overrightarrow{A B}+\overrightarrow{D K} \cdot \overrightarrow{B C}+\overrightarrow{K H} \cdot \overrightarrow{A C}$. Et d'après les résultats précédents : $\overrightarrow{D H} \cdot \overrightarrow{A C}=0+0+0=0$. 3. On a vu que $\overrightarrow{A H} \cdot \overrightarrow{C D}=0$.

Donc la droite $(\mathrm{AH})$ est orthogonale à la droite $(\mathrm{CD})$. Donc (AH) est la hauteur de ACD issue de A. Par ailleurs, on a vu que $\overrightarrow{D H} \cdot \overrightarrow{A C}=0$. Donc la droite $(\mathrm{DH})$ est orhtogonale à la droite $(\mathrm{AC})$. Donc (DH) est la hauteur de ACD issue de D. Le point H est situé à l'intersection de 2 hauteurs de ACD . Donc H est l'orthocentre du triangle ACD .

Exercice 2

ABCDEFGH est un cube dessiné ci-dessous.

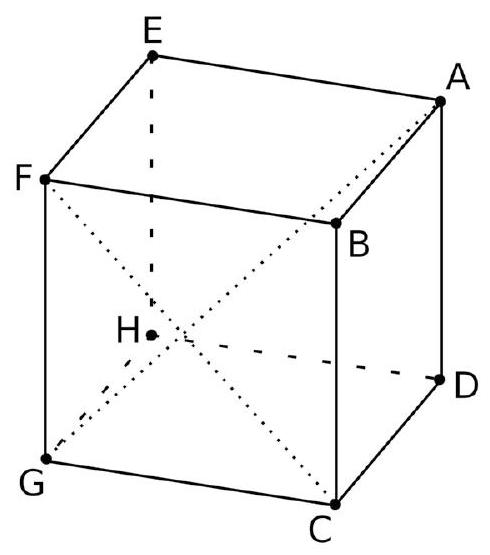
On veut démontrer que les droites (AG) et (CF) sont orthogonales.

1. Méthode vectorielle.

Montrer que : $\overrightarrow{C F} \cdot \overrightarrow{A B}=0$.

Montrer que $: \overrightarrow{C F} \cdot \overrightarrow{B G}=0$ ． Démontrer，en utilisant la relation de Chasles，que les vecteurs $\overrightarrow{C F}$ et $\overrightarrow{A G}$ sont orthogonaux． Conclure．

2．Méthode analytique．

Le plan est rapporté au repère（ $G, C, H, F$ ）． Donner，sans justifier，les coordonnées des points G，C，H，F，et A． Déterminer les coordonnées des vecteurs $\overrightarrow{C F}$ et $\overrightarrow{A G}$ ． Conclure．

Corrigé

1． ABCDEFGH est un cube，et par là ： l＇arête $[\mathrm{AB}]$ est orthogonale au plan（ BCG ），et donc à toute droite qu＇il contient，en particulier à la droite（ CF ）． Et par là，on obtient ： $\overrightarrow{C F} \cdot \overrightarrow{A B}=0$

ABCDEFGH est un cube，et par là ： BCGF est un carré，et ses diagonales［CF］et［BG］sont orthogonales； d＇où l＇égalité ： $\overrightarrow{C F} \cdot \overrightarrow{B G}=0$

Calculons le produit scalaire $\overrightarrow{C F} \cdot \overrightarrow{A G}$ ． $\overrightarrow{C F} \cdot \overrightarrow{A G}=\overrightarrow{C F} \cdot(\overrightarrow{A B}+\overrightarrow{B G}) \quad$（Chasles） Soit ： $\overrightarrow{C F} \cdot \overrightarrow{A G}=\overrightarrow{C F} \cdot \overrightarrow{A B}+\overrightarrow{C F} \cdot \overrightarrow{B G}$ ． Soit ： $\overrightarrow{C F} \cdot \overrightarrow{A G}=0+0 \quad$（d＇après（1）et（2））． Soit ： $\overrightarrow{C F} \cdot \overrightarrow{A G}=0$ ． Donc les vecteurs $\overrightarrow{C F}$ et $\overrightarrow{A G}$ sont orthogonaux． Et par là，les droites（ AG ）et（ CF ）sont orthogonales．

2．On a ：$\quad \mathrm{G}(0,0,0) \quad \mathrm{C}(1,0,0) \quad \mathrm{H}(0,1,0) \quad \mathrm{F}(0,0,1) \quad \mathrm{A}(1,1,1)$ ． On obtient alors ： $\overrightarrow{C F}(-1,0,1) \quad \overrightarrow{A G}(-1,-1,-1)$ ． Le repère est clairement orthonormé，et nous autorise à calculer des produits scalaires． $\overrightarrow{C F} \cdot \overrightarrow{A G}=(-1) \times(-1)+0 \times(-1)+1 \times(-1)=0$ ． Donc les vecteurs $\overrightarrow{C F}$ et $\overrightarrow{A G}$ sont orthogonaux． Et par là，les droites（ AG ）et（ CF ）sont orthogonales．

Exercice 3

ABCD est tétraèdre régulier. Ses faces sont des triangles équilatéraux de côté $x$.

Partie 1.

On veut démontrer que les arêtes $(\mathrm{AB})$ et $(\mathrm{CD})$ sont orthogonales. Montrer que : $\overrightarrow{A B} \cdot \overrightarrow{A D}=\frac{x^{2}}{2}$. Montrer que : $\overrightarrow{A B} \cdot \overrightarrow{A C}=\frac{x^{2}}{2}$. Démontrer, en utilisant la relation de Chasles, que $\overrightarrow{A B} \cdot \overrightarrow{C D}=0$. Puis conclure.

Partie 2.

Soit A ' le centre de gravité de BCD . Le point A' est défini par l'égalité : $\overrightarrow{A A^{\prime}}=\frac{1}{3}(\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A D})$.

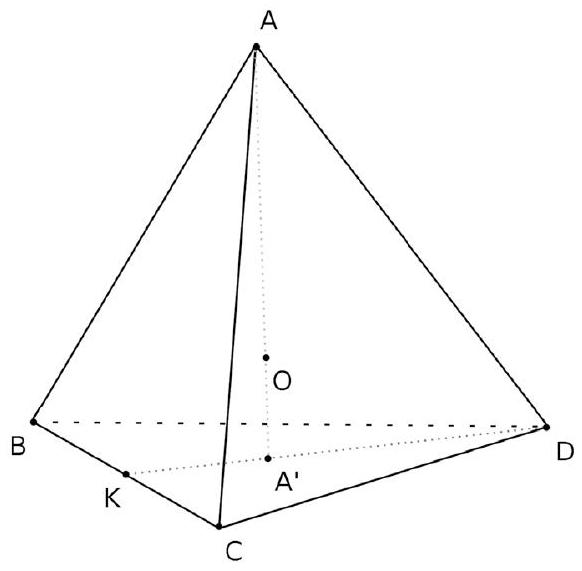
On veut montrer que la médiane ( AA ') du tétraèdre est aussi une hauteur de ce tétraèdre, c'est-à-dire que ( AA ') et le plan ( BCD ) sont orthogonaux. Déterminer la valeur de $\overrightarrow{A A^{\prime}} \cdot \overrightarrow{B C}$ et celle de $\overrightarrow{A A^{\prime}} \cdot \overrightarrow{B D}$. Conclure.

Partie 3.

Soit K le milieu de $[\mathrm{BC}]$. On a alors : $\overrightarrow{K A^{\prime}}=\frac{1}{3} \overrightarrow{K D}$. Montrer que $A A^{\prime}=\sqrt{\frac{2}{3}} \times x$

Partie 4.

Soit O le centre de gravité du tétraèdre. On a alors : $\overrightarrow{A^{\prime} O}=\frac{1}{4} \overrightarrow{A^{\prime} A}$.

Déterminer une valeur approchée arrondie à 0,1 degré de l'angle $\widehat{\mathrm{AOB}}$

Corrigé

Partie 1. $\overrightarrow{A B} \cdot \overrightarrow{A D}=A B \times A D \times \cos \widehat{\mathrm{BAD}}$. Et comme la face BAD du tétraèdre est équilatérale, on a : $\cos \widehat{\mathrm{BAD}}=\cos 60^{\circ}=\frac{1}{2}$. Donc on obtient : $\overrightarrow{A B} \cdot \overrightarrow{A D}=\frac{x^{2}}{2}$.

En raisonnant comme précédemment sur la face BAC , on obtient : $\overrightarrow{A B} \cdot \overrightarrow{A C}=A B \times A C \times \cos \widehat{\mathrm{BAC}}=\frac{x^{2}}{2}$.

Calculons le produit scalaire $\overrightarrow{A B} \cdot \overrightarrow{C D}$. $\overrightarrow{A B} \cdot \overrightarrow{C D}=\overrightarrow{A B} \cdot(\overrightarrow{C A}+\overrightarrow{A D}) \quad$ (Chasles) Soit : $\overrightarrow{A B} \cdot \overrightarrow{C D}=\overrightarrow{A B} \cdot \overrightarrow{C A}+\overrightarrow{A B} \cdot \overrightarrow{A D}=-\overrightarrow{A B} \cdot \overrightarrow{A C}+\overrightarrow{A B} \cdot \overrightarrow{A D}$. Soit : $\overrightarrow{A B} \cdot \overrightarrow{C D}=-\frac{x^{2}}{2}+\frac{x^{2}}{2}=0$. Et comme $\overrightarrow{A B} \cdot \overrightarrow{C D}=0$, les vecteurs $\overrightarrow{A B}$ et $\overrightarrow{C D}$ sont orthogonaux. Et par là, les droites $(\mathrm{AB})$ et $(\mathrm{CD})$ sont orthogonales.

Ce résultat se généralise sans difficulté : deux arêtes opposées d'un tétraèdre régulier sont orthogonales.

Partie 2.

On a : $\overrightarrow{A A^{\prime}} \cdot \overrightarrow{B C}=\frac{1}{3}(\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A D}) \cdot \overrightarrow{B C}$. $\overrightarrow{A A^{\prime}} \cdot \overrightarrow{B C}=\frac{1}{3}(\overrightarrow{A B} \cdot \overrightarrow{B C}+\overrightarrow{A C} \cdot \overrightarrow{B C}+\overrightarrow{A D} \cdot \overrightarrow{B C})$ Comme dans la partie 1., on obtient: $\overrightarrow{A B} \cdot \overrightarrow{B C}=-\overrightarrow{B A} \cdot \overrightarrow{B C}=-\frac{x^{2}}{2}$. $\overrightarrow{A C} \cdot \overrightarrow{B C}=\overrightarrow{C A} \cdot \overrightarrow{C B}=\frac{x^{2}}{2}$. Et comme on a vu précédemment que deux arêtes opposées sont orthogonales, on a : $\overrightarrow{A D} \cdot \overrightarrow{B C}=0$. Par conséquent, on obtient : $\overrightarrow{A A^{\prime}} \cdot \overrightarrow{B C}=\frac{1}{3}\left(-\frac{x^{2}}{2}+\frac{x^{2}}{2}+0\right)=0$. Donc les vecteurs $\overrightarrow{A A^{\prime}}$ et $\overrightarrow{B C}$ sont orthogonaux.

On montrerait de la même façon que $\overrightarrow{A A^{\prime}} \cdot \overrightarrow{B D}=0$, et par là, les vecteurs $\overrightarrow{A A^{\prime}}$ et $\overrightarrow{B D}$ sont orthogonaux.

Donc finalement, $\overrightarrow{A A^{\prime}}$ est orthogonal à $\overrightarrow{B C}$ et à $\overrightarrow{B D}$, qui sont clairement 2 vecteurs directeurs du plan (BCD). Donc (AA') et le plan (BCD) sont orthogonaux.

Ce résultat se généralise sans difficulté : médianes et hauteurs d'un tétraèdre régulier sont confondues.

Partie 3.

On a vu que (AA') et le plan (BCD) sont orthogonaux. Donc (AA') est orthogonale à toute droite du plan $(\mathrm{BCD})$, en particulier à la droite $\left(\mathrm{A}^{\prime} \mathrm{K}\right)$. Donc le triangle $\mathrm{AA}^{\prime} \mathrm{K}$ est rectangle en $\mathrm{A}^{\prime}$. Donc, par application du théorème de Pythagore, on a : $A A^{\prime 2}+A^{\prime} K^{2}=A K^{2}$. Or, comme $\overrightarrow{K A^{\prime}}=\frac{1}{3} \overrightarrow{K D}$, on a : $K A^{\prime}=\frac{1}{3} K D$. De plus, comme le tétraèdre est régulier, on a : $K D=K A$. Par conséquent, on obtient finalement : $A A^{\prime 2}+\left(\frac{1}{3} K A\right)^{2}=A K^{2}$. Et par là : $A A^{\prime 2}=\frac{8}{9} K A^{2}$

Dans le triangle équilatéral ABC , médiane et hauteur sont confondues. Le triangle AKC est donc rectangle en K . Donc, par application du théorème de Pythagore, on a : $A K^{2}+K C^{2}=A C^{2}$. Soit : $A K^{2}+\left(\frac{1}{2} x\right)^{2}=x^{2}$. Et donc : $A K^{2}=\frac{3}{4} x^{2}$. Et en reportant dans (1), on obtient : $A A^{\prime 2}=\frac{8}{9} \times \frac{3}{4} x^{2}$. Soit : $A A^{\prime}=\sqrt{\frac{2}{3}} \times x \quad$ c.q.f.d.

Partie 4.

On a vu que ( AA ') et le plan ( BCD ) sont orthogonaux. Donc ( AA ') est orthogonale à toute droite du plan $(\mathrm{BCD})$, en particulier à la droite $\left(\mathrm{A}^{\prime} \mathrm{B}\right)$. Donc le projeté orthogonal du vecteur $\overrightarrow{O B}$ sur le vecteur $\overrightarrow{O A}$ est le vecteur $\overrightarrow{O A^{\prime}}$.

Donc $: \overrightarrow{O A} \cdot \overrightarrow{O B}=\overrightarrow{O A} \cdot \overrightarrow{O A^{\prime}}$. Et comme $\overrightarrow{A^{\prime} O}=\frac{1}{4} \overrightarrow{A^{\prime} A}$, on obtient : Soit : $\overrightarrow{O A} \cdot \overrightarrow{O B}=\left(\frac{3}{4} \overrightarrow{A^{\prime} A}\right) \cdot\left(-\frac{1}{4} \overrightarrow{A^{\prime} A}\right)$. Soit : $\overrightarrow{O A} \cdot \overrightarrow{O B}=-\frac{3}{16} \times A A^{\prime 2} \quad$ (a).

Par ailleurs, on sait que : $\overrightarrow{O A} \cdot \overrightarrow{O B}=O A \times O B \times \cos \widehat{\mathrm{AOB}}$. Et il est clair que : $O A=O B=\frac{3}{4} A A^{\prime}$. On a donc : $\overrightarrow{O A} \cdot \overrightarrow{O B}=\frac{9}{16} A A^{\prime 2} \times \cos \widehat{\mathrm{AOB}}$ (b).

Donc finalement, par (a) et (b), on obtient: $\frac{9}{16} A A^{\prime 2} \times \cos \widehat{\mathrm{AOB}}=-\frac{3}{16} \times A A^{\prime 2}$. Et par là : $\cos \widehat{\mathrm{AOB}}=-\frac{1}{3}$. D'où : $\widehat{\mathrm{AOB}} \approx \mathbf{1 0 9 , 5}$ degrés (à la calculatrice).

Exercice 4

$P$ est un plan de l'espace, et S est un point de l'espace qui n'est pas dans $P$. Le projeté orthogonal de $S$ sur $P$ est le point $A$. $B$ est un point du plan $P$ distinct de $A$, et $C e 1$ est le cercle du plan $P$ de diamètre $[A B]$. $C$ est un point du cercle $C e 1$ distinct de A et de B . $H$ est le projeté orthogonal de $A$ sur la droite (SB). $K$ est le projeté orthogonal de $A$ sur la droite (SC).

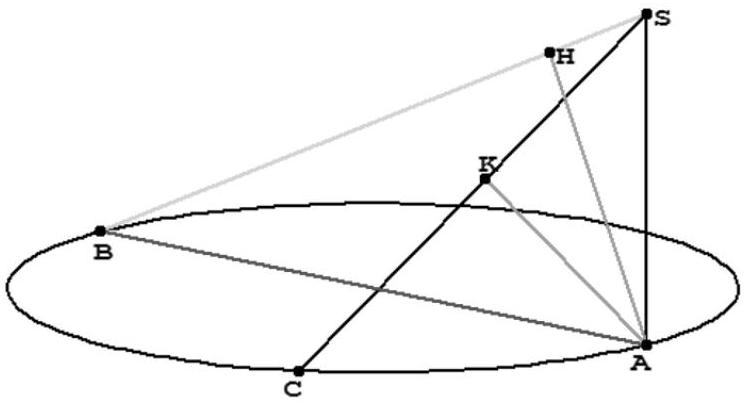
Attention ! La perspective masque les angles droits...

1. Montrer que : $\overrightarrow{C B}$ est normal au plan (ASC).
2. Montrer que : $\overrightarrow{A K}$ est normal au plan (BSC).
3. En utilisant la relation de Chasles et le résultat de la question 2., montrer que : $\overrightarrow{S B} \cdot \overrightarrow{H K}=0$.
4. Pourquoi a-t-on l'égalité : $\overrightarrow{A K} \cdot \overrightarrow{H K}=0$ ?
5. Montrer que le point K est sur le cercle Ce 2 de diamètre $[A H]$ contenu dans le plan perpendiculaire à $(\mathrm{SB})$ et passant par H .
6. Montrer que lorsque le point K lorsque C décrit tout le cercle Ce1 , alors K est sur le cercle Ce2.

Corrigé

1. Le plan (ASC) admet pour vecteurs directeurs $\overrightarrow{A C}$ et $\overrightarrow{A S}$.

Or, comme $C$ est sur le cercle $C e 1$ de diamètre $[A B]$, on a : $\overrightarrow{C B} \cdot \overrightarrow{A C}=0 \quad$ (a). Et comme $A$ est le projeté orthogonal de $S$ sur $P, \overrightarrow{A S}$ est orthogonal à tout vecteur appartenant à la direction du plan $P$. Et comme $B$ et $C$ sont tous les deux dans $P$, on obtient : $\overrightarrow{C B} \cdot \overrightarrow{A S}=0$ (b). Par conséquent, d'après (a) et (b), $\overrightarrow{C B}$ est orthogonal à deux vecteurs directeurs du plan (ASC). Donc $\overrightarrow{C B}$ est normal au plan (ASC). 2. Le plan (BSC) admet pour vecteurs directeurs $\overrightarrow{C B}$ et $\overrightarrow{C S}$.

Or $\overrightarrow{C B}$ est normal au plan (ASC) (d'après le 1.). Donc il est orthogonal à tout vecteur appartenant à la direction du plan (ASC), en particulier au vecteur $\overrightarrow{A K}$ (qui appartient évidemment à la direction du plan (ASC). On a donc $: \overrightarrow{A K} \cdot \overrightarrow{C B}=0$ (c). Par ailleurs, comme $K$ est le projeté orthogonal de $A$ sur la droite (SC), on a : $\overrightarrow{A K} \cdot \overrightarrow{C S}=0 \quad$ (d) . Par conséquent, d'après (c) et (d), $\overrightarrow{A K}$ est orthogonal à deux vecteurs directeurs du plan (BSC). Donc $\overrightarrow{A K}$ est normal au plan (BSC). 3. On a : $\overrightarrow{S B} \cdot \overrightarrow{H K}=\overrightarrow{S B} \cdot(\overrightarrow{H A}+\overrightarrow{A K})$ (Chasles).

Soit $: \overrightarrow{S B} \cdot \overrightarrow{H K}=\overrightarrow{S B} \cdot \overrightarrow{H A}+\overrightarrow{S B} \cdot \overrightarrow{A K}$. Or, comme $H$ est le projeté orthogonal de $A$ sur la droite (SB), on a : $\overrightarrow{S B} \cdot \overrightarrow{H A}=0$.

Et comme $\overrightarrow{A K}$ est normal au plan (BSC) (d'après le 2.), on a : $\overrightarrow{S B} \cdot \overrightarrow{A K}=0$. Par conséquent, on obtient : $\overrightarrow{S B} \cdot \overrightarrow{H K}=0+0=0$ c.q.f.d. 4. Comme $\overrightarrow{A K}$ est normal au plan (BSC) (d'après le 2.), il est orthogonal à tout vecteur appartenant à la direction du plan (BSC), en particulier, au vecteur $\overrightarrow{H K}$ (qui appartient évidemment à la direction du plan (BSC). Donc on a bien : $\overrightarrow{A K} \cdot \overrightarrow{H K}=0$. 5. Comme $\overrightarrow{S B} \cdot \overrightarrow{H K}=0$ (d'après le 3.), le point K est dans le plan perpendiculaire à (SB) et passant par H. Et comme $\overrightarrow{A K} \cdot \overrightarrow{H K}=0$, ce point K est sur le cercle Ce 2 de diamètre $[A H]$ contenu dans le plan perpendiculaire à $(\mathrm{SB})$ et passant par H. c.q.f.d. 6. On rappelle que les hypothèses précisent que le point $C$ est un point du cercle $C e 1$ distinct de A et de B . On vient donc de montrer que, si le point C est dans le cercle $C e 1$ privé des points $A$ et $B$, alors le point K est sur le cercle $C e 2$. Examinons le cas où C est en A . Le point K est alors en A , et le point K est donc bien sur le cercle Ce 2 . Examinons le cas où C est en B . Le point K est alors en H , et le point K est donc bien sur le cercle Ce 2 . Par conséquent, lorsque C décrit tout le cercle $C e 1, \mathrm{~K}$ est sur le cercle $C e 2$.

Exercice 5

Soient A et B deux points distincts de l'espace, et soit I le milieu de $[\mathrm{AB}]$. Soit P le plan passant par I et de vecteur normal $\overrightarrow{A B}$. Le plan P s'appelle plan médiateur du segment $[\mathrm{AB}]$.

1. Soit M un point quelconque de P .

Si M est en I , alors il est évident que $A M=M B$. Supposons que $M$ soit distinct de I. On peut alors considérer le plan (ABM). Montrer que M appartient à la médiatrice de $[\mathrm{AB}]$ dans le plan ( ABM ). Qu'en déduire concernant AM et MB ? 2. Démontrons la réciproque.

Supposons cette fois que M est un point de l'espace tel que $A M=M B$. Si $M$ est en $I$, alors il est évident que $M$ est sur $P$. Supposons que M soit distinct de I. On peut alors considérer le plan (ABM) si besoin. Montrer que M appartient à P . 3. Reprenons le tétraèdre régulier ABCD de l'exercice 3. Montrer en utilisant un plan médiateur que les arêtes $(\mathrm{AB})$ et $(\mathrm{CD})$ sont orthogonales.

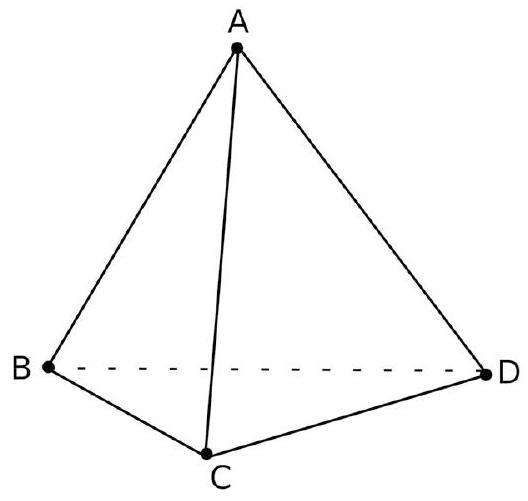
Corrigé

1. Soit M un point quelconque de P .

Comme I est dans $\mathrm{P}, \overrightarrow{M I}$ est un vecteur appartenant à la direction de P . Et comme le plan P a pour vecteur normal $\overrightarrow{A B}$, les vecteurs $\overrightarrow{A B}$ et $\overrightarrow{M I}$ sont orthogonaux. Par conséquent, dans le plan $(\mathrm{ABM})$, la droite $(\mathrm{MI})$ est perpendiculaire à $[\mathrm{AB}]$.

Et comme elle passe par son milieu I, c'est la médiatrice de [AB] dans le plan (ABM). Et donc $A M=M B$. 2. M est un point de l'espace distinct de I tel que $A M=M B$.

Donc, dans le plan $(\mathrm{ABM}), \mathrm{M}$ appartient à la médiatrice de $[\mathrm{AB}]$. Or I, milieu de $[\mathrm{AB}]$, est clairement sur la médiatrice de $[\mathrm{AB}]$. Donc la médiatrice de $[\mathrm{AB}]$ est la droite (MI). Et par là, les vecteurs $\overrightarrow{A B}$ et $\overrightarrow{M I}$ sont orthogonaux. Or P est le plan passant par I et de vecteur normal $\overrightarrow{A B}$. Donc M appartient à P . 3. Reprenons le tétraèdre régulier ABCD de l'exercice 3.

Le tétraèdre ABCD est régulier, donc : $D A=C A$, et donc A appartient au plan médiateur de $[\mathrm{CD}]$. De même, $D B=C B$, et donc B appartient au plan médiateur de $[\mathrm{CD}]$. Donc $\overrightarrow{A B}$ appartient à la direction de ce plan médiateur. Or ce plan médiateur a pour vecteur normal $\overrightarrow{C D}$. Donc $\overrightarrow{C D}$ est orthogonal à tout vecteur de la direction de ce plan médiateur, en particulier à $\overrightarrow{A B}$. Donc les arêtes $(\mathrm{AB})$ et $(\mathrm{CD})$ sont orthogonales.

Exercice 6

L'espace est rapporté au repère orthonormal ( $\mathrm{O}, \mathrm{I}, \mathrm{J}, \mathrm{K}$ ). On considère les points $M(0,5 ; 0 ; 0,5), N(0 ; 1 ; 0,5), P(1 ; 1 ; 0)$ et $A(1 ; 1 ; 1)$.

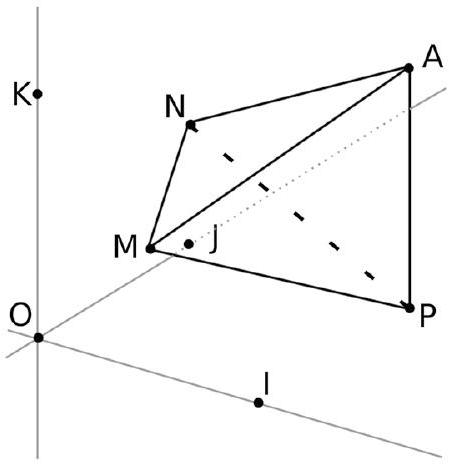
1. Soit $\vec{n}(a ; 1 ; b)$ un vecteur orthogonal à $\overrightarrow{M P}$ et $\overrightarrow{M N}$.

Déterminer les valeurs de $a$ et $b$. 2. Montrer que le point $R(x ; y ; z)$ appartient au plan (MNP) si et seulement si $2 x+y+4 z-3=0$ 3. Expliquer pourquoi le point $S(x ; y ; z)$ appartient à la droite $d$ passant par A et orthogonale au plan ( $M N P$ ) si et seulement si il existe un réel $t$ tel que $\left{\begin{array}{c}x=1+2 t \ y=1+t \ z=1+4 t\end{array}\right.$ 4. Déterminer les coordonnées du point H , projeté orthogonal de A sur (MNP). Placer le point $H$ sur le dessin. 5. On admet que l'aire du triangle MNP vaut environ 0,57 unités d'aires. Calculer le volume du tétraèdre AMNP .

Corrigé

1. On obtient facilement : $\overrightarrow{M P}(0.5 ; 1 ;-0.5)$ et $\overrightarrow{M N}(-0.5 ; 1 ; 0)$.

Le repère étant orthonormé, on obtient : $\overrightarrow{M P} \cdot \vec{n}=0.5 a+1-0.5 b$ et $\overrightarrow{M N} \cdot \vec{n}=-0.5 a+1$.

Par conséquent : $\vec{n}(a ; 1 ; b)$ est orthogonal à $\overrightarrow{M P}$ et $\overrightarrow{M N}$. $\Leftrightarrow\left{\begin{array}{c}0.5 a+1-0.5 b=0 \ -0.5 a+1=0\end{array} \Leftrightarrow\left{\begin{array}{c}0.5 a+1-0.5 b=0 \ a=2\end{array}\right.\right.$ $\Leftrightarrow\left{\begin{array}{l}b=4 \ a=2\end{array}\right.$ Et par là, on obtient: $\vec{n}(2 ; 1 ; 4)$ 2. $\vec{n}$ un vecteur orthogonal à deux vecteurs $\overrightarrow{M P}$ et $\overrightarrow{M N}$ non colinéaires (car leurs coordonnées ne sont pas proportionnelles). Or ces deux vecteurs appartiennent à la direction du plan (MNP). Donc $\vec{n}$ est un vecteur normal au plan (MNP). Par conséquent, le point $R(x ; y ; z)$ appartient au plan $(M N P)$ si et seulement si $\overrightarrow{M R} \cdot \vec{n}=0$. Or on obtient facilement : $\overrightarrow{M R}(x-0.5 ; y ; z-0.5)$, et on sait que : $\vec{n}(2 ; 1 ; 4)$.

Donc : $R(x ; y ; z) \in(M N P) \Leftrightarrow 2(x-0.5)+1 y+4(z-0.5)=0 \Leftrightarrow$ $2 x-1+y+4 z-2=0$.

Et finalement : $R(x ; y ; z) \in(M N P) \Leftrightarrow 2 x+y+4 z-3=0$.

Pour information, cette égalité s'appelle une «équation cartésienne» du plan (MNP) (voir le chapitre suivant). 3. Comme $\vec{n}$ est un vecteur normal au plan (MNP), le point $S(x ; y ; z)$ appartient à la droite $d$ passant par A et orthogonale au plan (MNP) si et seulement si $\overrightarrow{A S}$ et $\vec{n}$ sont colinéaires. Donc $S(x ; y ; z) \in d \Leftrightarrow$ il existe un réel $t$ tel que $\overrightarrow{A S}=t \vec{n}$. Et comme on a: $\overrightarrow{A S}(x-1 ; y-1 ; z-1)$ et $\vec{n}(2 ; 1 ; 4)$, on obtient : $S(x ; y ; z) \in d \Leftrightarrow$ il existe un réel $t$ tel que $\left{\begin{array}{l}x-1=2 t \ y-1=t \ z-1=4 t\end{array}\right.$ Soit : $S(x ; y ; z) \in d \Leftrightarrow$ il existe un réel $t$ tel que $\left{\begin{array}{c}x=1+2 t \ y=1+t \ z=1+4 t\end{array}\right.$

Pour information, ce système donne une «représentation paramétrique» de la droite d (voir le chapitre suivant). 4. Comme la droite $d$ passe par A et est orthogonale au plan ( $M N P$ ), le point H , projeté orthogonal de A sur (MNP), est situé à l'intersection de $d$ et de (MNP). Par conséquent, ses coordonnées ( $x ; y ; z$ ) vérifient l'équation cartésienne du plan et la représentation paramétrique de la droite. Par substitution, on obtient alors : (E) $2(1+2 t)+(1+t)+4(1+4 t)-3=0$.

Or : (E) $\Leftrightarrow 2+4 t+1+t+4+16 t-3=0 \Leftrightarrow t=-\frac{4}{21}$. Donc les coordonnées de H sont : $\left{\begin{array}{c}x=1+2 \times\left(-\frac{4}{21}\right)=\frac{13}{21} \approx 0.6 \ y=1+\left(-\frac{4}{21}\right)=\frac{17}{21} \approx 0.8 \ z=1+4 \times\left(-\frac{4}{21}\right)=\frac{5}{21} \approx 0.2\end{array}\right.$ Donc : $H\left(\frac{13}{21} ; \frac{17}{21} ; \frac{5}{21}\right)$.

On a placé le point H sur le dessin qui suit. 5. Le volume d'un tétraèdre est donné par la formule : $\frac{b \times h}{3}$, où $b$ est l'aire d'une base et $h$ la longueur de la hauteur correspondante. Ici, la base sera la face MNP et la hauteur sera évidemment [AH]. On a: $b \approx 0,57$. Or, on obtient : $\overrightarrow{A H}\left(-\frac{8}{21} ;-\frac{4}{21} ;-\frac{16}{21}\right)$, et donc : $A H=\sqrt{\left(-\frac{8}{21}\right)^{2}+\left(-\frac{4}{21}\right)^{2}+\left(-\frac{16}{21}\right)^{2}}=4 \frac{\sqrt{21}}{21} \approx 0,87$. Et donc le volume cherché est environ égal à : $\frac{0,57 \times 0,87}{3} \approx 0,17$.

Exercice 7

L'espace est rapporté au repère orthonormal ( $\mathrm{O}, \mathrm{I}, \mathrm{J}, \mathrm{K}$ ). On considère les points $A(4 ; 2 ; 0), B(-1 ; 0 ; 0)$ et $R(2 ; 1 ; 0)$.

1. Montrer que le point $M(x ; y ; z)$ appartient à la sphère S de centre R de rayon 3 si et seulement si $x^{2}-4 x+y^{2}-2 y+z^{2}-4=0$. Pour information, cette égalité s'appelle une «équation cartésienne» de la sphère $S$.
2. Montrer que le point $M(x ; y ; z)$ appartient à la sphère S de centre R de rayon 3 si et seulement si $\overrightarrow{O M} \cdot \overrightarrow{A M}=4$
3. Montrer que le point $B(-1 ; 1 ; 0)$ appartient à la sphère S .
4. Déterminer l'abscisse $a$ du point $C(a ; 1 ; 0)$, distinct de B , qui appartient aussi à la sphère S .
5. $D$ est le point tel que $R$ soit le milieu de $[B D]$. Et par là, $D$ est le point de la sphère S opposé à B . Montrer que $D$ et $C$ sont confondus.
6. Montrer que le point $M(x ; y ; z)$ appartient à la sphère S si et seulement si $\overrightarrow{B M} \cdot \overrightarrow{D M}=0$

Corrigé

1. On obtient facilement: $\overrightarrow{R M}(x-2 ; y-1 ; z)$.

Le repère étant orthonormé, on obtient : $R M=\sqrt{(x-2)^{2}+(y-1)^{2}+z^{2}}$.

Par conséquent : $M$ appartient à la sphère S de centre R de rayon 3 . $\Leftrightarrow \sqrt{(x-2)^{2}+(y-1)^{2}+z^{2}}=3$. $\Leftrightarrow(x-2)^{2}+(y-1)^{2}+z^{2}=9$. $\Leftrightarrow x^{2}-4 x+4+y^{2}-2 y+1+z^{2}-9=0$. $\Leftrightarrow x^{2}-4 x+y^{2}-2 y+z^{2}-4=0 \quad$ c.q.f.d. 2. On obtient facilement : $\overrightarrow{O M}(x ; y ; z)$ et $\overrightarrow{A M}(x-4 ; y-2 ; z)$.

Le repère étant orthonormé, on obtient : $\overrightarrow{O M} \cdot \overrightarrow{A M}=x(x-4)+y(y-2)+z^{2}$.

Par conséquent $: \overrightarrow{O M} \cdot \overrightarrow{A M}=4$. $\Leftrightarrow x(x-4)+y(y-2)+z^{2}=4$. $\Leftrightarrow x^{2}-4 x+y^{2}-2 y+z^{2}-4=0$. $\Leftrightarrow M$ appartient à la sphère S de centre K de rayon 3 (d'après le 1.). Et par là : $M \in \mathrm{~S} \Leftrightarrow \overrightarrow{O M} \cdot \overrightarrow{A M}=4 \quad$ c.q.f.d. 3. On calcule : $x_{B}^{2}-4 x_{B}+y_{B}^{2}-2 y_{B}+z_{B}^{2}-4=(-1)^{2}-4 \times(-1)+1^{2}-2 \times 1+0^{2}-4$

Soit: $x_{B}^{2}-4 x_{B}+y_{B}{ }^{2}-2 y_{B}+z_{B}{ }^{2}-4=0$. Donc le point $B(-1 ; 1 ; 0)$ appartient à la sphère $S$ 4. $C(a ; 1 ; 0) \in \mathrm{S} \Leftrightarrow a^{2}-4 a+1^{2}-2 \times 1+0^{2}-4=0$.

Soit : $C(a ; 1 ; 0) \in \mathrm{S} \Leftrightarrow a^{2}-4 a-5=0$. Les racines du trinôme du second degré sont -1 et 5 . Comme $C$ est distinct de $B$, on obtient : $C(5 ; 1 ; 0)$. 5. R est le milieu de $[\mathrm{BD}]$, donc $: \overrightarrow{R D}=\overrightarrow{B R}$.

Et par là : $\left{\begin{aligned} x-2 & =2-(-1) \ y-1 & =1-1 \ z & =0\end{aligned}\right.$ D'où : $x=5$ et $y=1$ et $z=0$. Donc on a : $D(5 ; 1 ; 0)$. On constate que D et C sont confondus. c.q.f.d. 6. On obtient facilement : $\overrightarrow{B M}(x+1 ; y-1 ; z)$ et $\overrightarrow{D M}(x-5 ; y-1 ; z)$.

Le repère étant orthonormé, on obtient : $\overrightarrow{B M} \cdot \overrightarrow{D M}=(x+1)(x-5)+(y-1)(y-1)+z^{2}$. Soit : $\overrightarrow{B M} \cdot \overrightarrow{D M}=x^{2}-5 x+x-5+y^{2}-2 y+1+z^{2}$. Soit : $\overrightarrow{B M} \cdot \overrightarrow{D M}=x^{2}-4 x+y^{2}-2 y+z^{2}-4$. Par conséquent : $\overrightarrow{B M} \cdot \overrightarrow{D M}=0 \Leftrightarrow x^{2}-4 x+y^{2}-2 y+z^{2}-4=0$. On reconnaît, d'après le 1 ., une équation cartésienne de S . Donc le point $M(x ; y ; z)$ appartient à la sphère S si et seulement si $\overrightarrow{B M} \cdot \overrightarrow{D M}=0$

c.q.f.d.