Exercices corrigés

Exercices corrigés

Exercice 1

1. Montrer que, si $x \geq 0$, alors $2 e^{2 x+1}-1>0$.
2. Soit $f$ la fonction définie sur $[0 ; 1] \operatorname{par} f(x)=e^{2 x+1}-x$.

Montrer que l'équation $f(x)=10$ admet une solution unique $\alpha$ sur $[0 ; 1]$. 3. Compléter le programme suivant (lignes 8 et 10 ) pour que la fonction sol_balayage(delta) retourne une liste de deux nombres $a$ et $b$ encadrant $\alpha$ et vérifiant $|b-a| \approx$ delta.

1 from math import exp
2
3def f(x):
    return exp(2*x+1)-x
6def sol_balayage(delta):
    a=0
    while f(a)
        a=a+delta
    return []
print(sol_balayage(0.01))

Après exécution du programme, que s'affiche-t-il dans la console ? 4. Compléter le programme suivant (lignes 10,11 et 15 ) pour que la fonction sol_dichotomie(delta) retourne une liste de deux nombres $a$ et $b$ encadrant $\alpha$ et vérifiant $|b-a| \leq$ delta.

1 from math import exp
2
3def f(x):
    return exp(2*x+1)-x
5
6def sol_dichotomie(delta):
    a=0
    b=1
    m=(a+b)/2
    while b-a
        if f(m)
            b=m
        else:
            a=m
        m=
    return [a,b]
print(sol_dichotomie(0.01))

Après exécution du programme, que s'affiche-t-il dans la console ?

Corrigé

1. Si $x \geq 0$, alors $2 x+1 \geq 2 \times 0+1$. Soit : $2 x+1 \geq 1$.

Donc : $e^{2 x+1} \geq e^{1}$ (par croissance de la fonction exponentielle). Et par là : $2 e^{2 x+1}-1 \geq 2 \times e-1$.

Et comme $2 e-1 \approx 4,4$, on obtient : $2 e^{2 x+1}-1>0$. 2. Soit $f$ la fonction définie sur $[0 ; 1] \operatorname{par} f(x)=e^{2 x+1}-x$.

On a : $f^{\prime}(x)=2 e^{2 x+1}-1$. Et par là, d'après le résultat précédent, la fonction $f^{\prime}$ est strictement positive. Par conséquent, $f$ est strictement croissante sur $[0 ; 1]$. Or, $f$ est continue (elle résulte d'opérations et de composée de fonctions continues). Et de plus, 10 est compris entre $f(0) \approx 2,7$ et $f(1) \approx 19,1$. Les 3 conditions du théorème de la bijection sont vérifiées. Donc l'équation $f(x)=10$ admet une unique solution $\alpha$ sur [ $0 ; 1$ ]. 3. Voici le programme complété.

l from math import exp
2
}def f(x):
    return exp(2*x+1)-x
def sol_balayage(delta):
    a=0
    while f(a)<10:
        a=a+delta
    return [a-delta,a]
print(sol_balayage(0.01))

Il s'affiche [ $\mathbf{0 . 6 8 0 0 0 0 0 0 0 0 0 0 0 0 0 4 , ~} \mathbf{0 . 6 9 0 0 0 0 0 0 0 0 0 0 0 0 0 4 ]}$ après exécution. On a : delta $=0,01, a \approx 0.68$ et $b \approx 0.69$. On note que : $|b-a| \approx 0,01$, et par là, on a bien : $|b-a| \approx$ delta. L'algorithme utilisé pour encadrer $\alpha$ est un algorithme de balayage (l'intervalle d'encadrement est balayé progressivement jusqu'à détection de l'encadrement désiré). 4. Voici le programme complété.

from math import exp
2
}def f(x):
    return exp(2*x+1)-x
5
6def sol_dichotomie(delta):
    a=0
    b=1
    m=(a+b)/2
    while b-a>delta:
        if f(m)>10:
            b=m
        else:
            a=m
        m=(a+b)/2
    return [a,b]
print(sol_dichotomie(0.01))

Il s'affiche [ $\mathbf{0 . 6 7 9 6 8 7 5 , 0 . 6 8 7 5 ]}$ après exécution. On a : delta $=0,01, a \approx 0,6796875$ et $b \approx 0,6875$. On note que : $|b-a| \approx 0,008$, et par là, on a bien : $|b-a| \leq$ delta.

L'algorithme utilisé pour encadrer $\alpha$ est un algorithme de dichotomie (l'intervalle d'encadrement a été coupé en deux à chaque itération).

Exercice 2

Soit $f$ la fonction définie sur [1;2] par $f(x)=x^{3}+x$. Montrer que l'équation $f(x)=5$ admet une solution unique $\alpha$ sur [1;2], puis déterminer un encadrement de $\alpha$ d'amplitude 0,1 .

Corrigé

$f^{\prime}(x)=3 x^{2}+1$. Étudions le signe de cette dérivée. $x^{2} \geq 0$ (c'est un carré). Donc $3 x^{2} \geq 0$, et par là: $3 x^{2}+1>0$. D'où le tableau de variation de $f$ ci-contre. D'après ce tableau de variation, la fonction $f$ est continue et strictement croissante sur [1;2]. Or 5 est un nombre compris entre $f(1)=2$ et $f(2)=10$, Donc, d'après le théorème de la bijection, l'équation $f(x)=5$ admet une unique solution $\alpha$ sur [1;2].

$x$	1		2
$f^{\prime}(x)$		+
			10
$f(x)$
		2

Déterminons un encadrement de $\alpha$ par essais successifs à l'aide de la calculatrice. Nous remplissons ainsi le tableau de valeurs suivant (où les valeurs sont arrondies à $10^{-3}$ près).

$x$	1	2	1,5	1,7	1,6
$f(x)$	2	10	4,875	6,613	5,695

L'encadrement cherché est : $1,5<\alpha<1,6$. Et comme $1,6-1,5=0,1$, l'amplitude est bien égale à 0,1 .

Exercice 3

Soit $f$ la fonction définie sur $[0 ;+\infty[$ et vérifiant le tableau de variations ci-après.

On sait de plus que $f(100)=3$. Montrer que l'équation $f(x)=50$ admet une solution unique sur $[0 ;+\infty[$.

$x$	0		$+\infty$
$f^{\prime}(x)$		-
	200
$f(x)$

Corrigé

D'après ce tableau de variation, la fonction $f$ est continue et strictement décroissante sur $[0 ;+\infty[$, et donc en particulier sur $[0 ; 100]$. Or 50 est un nombre compris entre $f(0)=200$ et $f(100)=3$, Donc, d'après le théorème de la bijection, l'équation $f(x)=50$ admet une unique solution sur [0; 100]. De plus, comme $f$ est strictement décroissante sur $[0 ; \infty[$, si $x>100$, alors $f(x)<f(100)$. C'est-à-dire que si $x>100$, alors $f(x)<3$. Par conséquent, l'équation $f(x)=50$ ne peut avoir de solution sur $] 100 ; \infty[$. Finalement, l'équation $f(x)=50$ admet une solution unique sur $[0 ; \infty[$.

Exercice 4

Soit $f$ la fonction définie sur $[0 ; 10]$ telle que $f(0)=30$ et $f(10)=2$. Est-il certain que les propositions suivantes soient vraies ? (inutile de justifier) Lorsqu'une proposition est fausse, tracer la courbe représentative d'une fonction $f$ présentant un contre-exemple.

1. L'équation $f(x)=15$ admet au moins une solution sur [ $0 ; 10$ ].
2. L'équation $f(x)=15$ admet une unique solution sur [ $0 ; 10$ ].
3. L'équation $f(x)=50$ n'admet pas de solution sur [ $0 ; 10$ ].

Corrigé

Toutes les propositions peuvent être fausses. Figure 1 ci-après : L'équation $f(x)=15$ n'admet pas de solution sur [ $0 ; 10$ ]. Remarquons que ni le théorème des valeurs intermédiaires, ni le théorème de la bijection ne peuvent s'appliquer car $f$ n'est pas continue sur $[0 ; 10]$.

Figure 2 ci-après : L'équation $f(x)=15$ admet cinq solutions sur [ $0 ; 10$ ].

Remarquons que le théorème de la bijection ne peut s'appliquer car $f$ n'est pas strictement monotone sur [ $0 ; 10$ ].

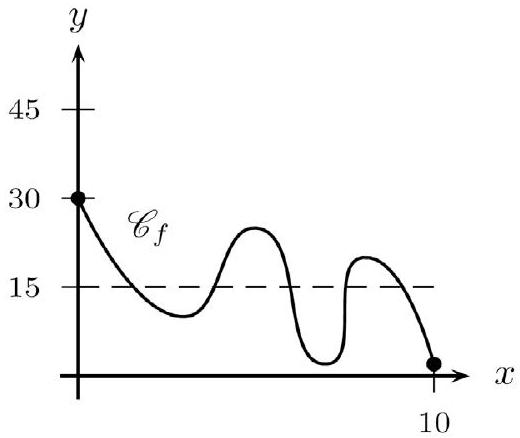
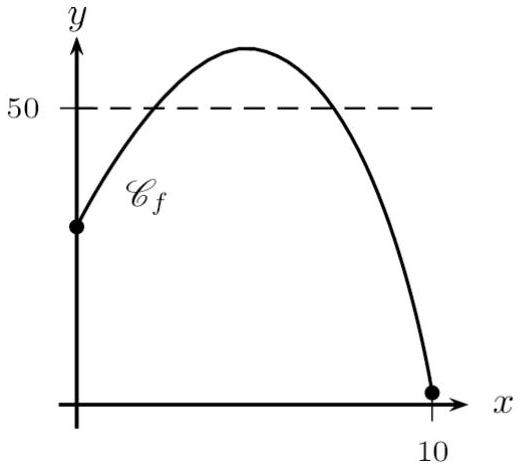
Figure 3 ci-après : L'équation $f(x)=50$ admet deux solutions sur [ $0 ; 10$ ]. Remarquons que ceci n'est démontrable ni avec le théorème des valeurs intermédiaires, ni avec le théorème de la bijection; ces théorèmes ne peuvent s'appliquer car le nombre 50 n'est pas entre $f(0)$ et $f(10)$.

Exercice 5

Cet exercice utilise aussi le cours sur les limites. Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x)=2(x-1) e^{x}+1$. 1.a. Déterminer $\lim {x \rightarrow+\infty} f(x)$. 1.b. Montrer que la droite $d$ d'équation $y=1$ est asymptote à $\mathrm{C}{f}$ en $-\infty$. 1.c. Déterminer la position de $\mathrm{C}_{f}$ par rapport à $d$. 2. Calculer la dérivée de $f$ et déterminer son signe. 3. Dresser le tableau de variation de $f$ et préciser la valeur de $f(0)$. 4. Soit (1) l'équation $f(x)=0$.

Démontrer que l'équation (1) admet exactement 2 solutions dans $\mathbb{R}$. 5. Soit $a$ la solution négative de (1), et $b$ la solution positive de (1).

À l'aide d'une calculatrice, donner les valeurs de $a$ et $b$ arrondies au centième.

Corrigé

1.a. Comme $2>0$ et $\lim _{x \rightarrow+\infty} x-1=+\infty$ et $\lim _{x \rightarrow+\infty} e^{x}=+\infty$, on en déduit que $\lim _{x \rightarrow+\infty} 2(x-1) e^{x}=+\infty$ (limite d'un produit). Et comme $\lim _{x \rightarrow+\infty} 1=1$, on obtient $\lim {x \rightarrow+\infty} f(x)=+\infty$ (limite d'une somme). 1.b. Pour montrer que la droite $d$ d'équation $y=1$ est asymptote à $\mathrm{C}{f}$ en $-\infty$, il suffit de montrer que $\lim {x \rightarrow-\infty} f(x)=1$. Pour lever l'indétermination en $-\infty$, on développe $f(x)$. On a $f(x)=2 x e^{x}-2 e^{x}+1$. On sait que $\lim {x \rightarrow-\infty} x e^{x}=0, \lim {x \rightarrow-\infty} e^{x}=0$, et $\lim {x \rightarrow-\infty} 1=1$. D'où $\lim {x \rightarrow-\infty} f(x)=2 \times 0-2 \times 0+1=1$. Donc $d$ est bien asymptote à $\mathrm{C}{f}$ en $-\infty$, 1.c. Pour étudier la position de $C{f}$ (d'équation $y=f(x)$ ) par rapport à d (d'équation $y=1$ ), on détermine le signe de $\delta=f(x)-1$. On a : $\delta=f(x)-1=2(x-1) e^{x}+1-1=2(x-1) e^{x}$. Or $2>0$, et $e^{x}>0$. Donc le produit $\delta=2(x-1) e^{x}$ est du signe de $x-1$. Si $x<1$, alors $\delta<0$, et par là, $\mathrm{C}{f}$ est en dessous de $d$. Si $x=1$, alors $\delta=0$, et $C{f}$ et $d$ sont sécantes. Si $x>1$, alors $\delta>0$, et par là, $\mathrm{C}{f}$ est au-dessusde $d$. 2. On pose $f=u v+1$ avec $u=2(x-1)$ et $v=e^{x}$.

D'où $f^{\prime}=u^{\prime} v+u v^{\prime}+0$ avec $u^{\prime}=2 \times 1=2$ et $v^{\prime}=e^{x}$. Donc $f^{\prime}(x)=2 e^{x}+2(x-1) e^{x}=2(1+x-1) e^{x}=2 x e^{x}$. Comme 2 et $e^{x}$ sont strictement positifs, $f^{\prime}(x)$ est du signe de $x$. Donc $f^{\prime}$ est strictement négative sur $]-\infty ; 0[$, nulle en 0 , et strictement positive sur $] 0 ;+\infty[$. 3. Notons que $f(0)=2 \times(0-1) e^{0}+1=-2+1=-1$.

On donne ci-dessous le tableau de variation de $f$. On y a reporté les limites trouvées à la question 1.

$x$	$-\infty$		0		$+\infty$
$f^{\prime}(x)$		-	0	+
	1
$f(x)$
				-1

4. D'après ce tableau de variation, la fonction $f$ est continue et strictement décroissante sur $]-\infty ; 0$ ]. Or, comme $\lim _{x \rightarrow-\infty} f(x)=1$ et $f(0)=-1$, on a : $\lim _{x \rightarrow-\infty} f(x)>0>f(0)$. Donc, d'après le théorème de la bijection, l'équation $f(x)=0$ admet une unique solution a sur ] - $\infty$; 0].

D'après ce tableau de variation, la fonction $f$ est continue et strictement croissante sur $[0 ;+\infty[$. Or on a : $f(0)<0$ et $\lim _{x \rightarrow+\infty} f(x)=+\infty$. Donc, d'après le théorème de la bijection, l'équation $f(x)=0$ admet une unique solution $b$ sur $[0 ;+\infty[$.

Finalement, l'équation (1) admet exactement 2 solutions dans $\mathbb{R}$. 5. À l'aide d'une calculatrice, on obtient : $f(-1,68) \approx 1.10^{-3}$ et $f(-1,675) \approx-2.10^{-3}$ et $f(-1,67) \approx-5.10^{-3}$. D'où $a \approx-1,68$ (arrondie au centième). $f(0,76) \approx-0,026$ et $f(0,765) \approx-0,01$ et $f(0,77) \approx 6,5.10^{-3}$. D'où $b \approx 0,77$ (arrondie au centième).

Exercice 6

1. Soit $f$ définie sur $[0 ;+\infty[\operatorname{par} f(x)==\sqrt{4+3 x}$.

Pourquoi $f$ est-elle continue ? 2. Déterminer le sens de variation de $f$. 3. Soit $\left(u_{n}\right)$ une suite définie par : $u_{0}=1$, et par la relation de récurrence $u_{n+1}=\sqrt{4+3 u_{n}}$ (pour tout naturel $n$ ). Il est clair que tous les termes de cette suite sont strictement positifs. Montrer que $u_{1}-u_{0}>0$. 4. Montrer par récurrence que, pour tout naturel $n, u_{n+1}-u_{n}>0$. 5. En déduire le sens de variation de $\left(u_{n}\right)$. 6. On suppose que $\lim {n \rightarrow+\infty} u{n}=l$ avec $l$ dans $[0 ;+\infty[$. Montrer que la seule valeur possible pour $l$ est 4 . 7. Montrer que, pour tout naturel $n, u_{n+1}-4=\frac{3\left(u_{n}-4\right)}{u_{n+1}+4}$. 8. Montrer par récurrence que, pour tout naturel $n, u_{n} \leq 4$. 9. Montrer que ( $u_{n}$ ) est convergente et donner sa limite. .

Corrigé

1. $f$ est définie sur $[0 ;+\infty[\operatorname{par} f(x)==\sqrt{4+3 x}$.

Et $f$ est obtenue par opérations ou par composition de fonctions usuelles. Donc $f$ est continue sur $[0 ;+\infty[$. 2. On a: $f(x)==\sqrt{4+3 x}$. $f^{\prime}(x)=3 \frac{1}{2 \sqrt{4+3 x}}=\frac{3}{2 \sqrt{4+3 x}}$. $f^{\prime}$ est clairement strictement positive, et par là, $f$ est strictement croissante. 3. On a: $u_{1}=\sqrt{4+3 \times u_{0}}=\sqrt{7}$, et donc : $u_{1}-u_{0}=\sqrt{7}-1 \approx 1,6$.

Donc : $u_{1}-u_{0}>0$. 4. Soit $P_{n}$ la propriété $u_{n+1}-u_{n}>0$.

Montrons par récurrence que, pour tout entier naturel $n, P_{n}$ est vraie. Initialisation : On a : $u_{1}-u_{0}>0$, donc $P_{0}$ est vraie.

Hérédité : Soit $n$ un entier naturel, supposons que $P_{n}$ soit vraie. On a donc: $u_{n+1}-u_{n}>0$. Et, comme $f$ est strictement croissante sur $[0 ;+\infty[$, et que les 2 termes sont bien dans $\left[0 ;+\infty\left[\right.\right.$, on obtient: $f\left(u_{n+1}\right)-f\left(u_{n}\right)>0$. Soit : $u_{n+2}-u_{n+1}>0$. Et par là : $P_{n+1}$ est vraie. Conclusion : pour tout naturel $n, u_{n+1}-u_{n}>0$. 5. Donc la suite $\left(u_{n}\right)$ est strictement croissante. 6. On suppose que $\lim {n \rightarrow+\infty} u{n}=l$.

Or ici, $u_{n+1}=f\left(u_{n}\right)$ avec $f(x)=\sqrt{4+3 x}$. Donc, comme $f$ est continue, par passage à la limite, on obtient: $l=\sqrt{4+3 l}$. Soit: $l^{2}=4+3 l$. Soit : $l^{2}-3 l-4=0$. -1 est racine évidente du trinôme. Or le produit des racines est $\frac{c}{a}=\frac{-4}{1}=-4$. Donc la seconde racine est 4 . Et par là : $l=-1$ ou $l=4$. Or il est impossible qu'une suite strictement positive ait une limite strictement négative. Donc la seule valeur possible pour $l$ est 4 . 7. On a : $u_{n+1}-4=\sqrt{4+3 u_{n}}-4=\frac{\left(\sqrt{4+3 u_{n}}-4\right)\left(\sqrt{4+3 u_{n}}+4\right)}{\sqrt{4+3 u_{n}}+4}$.

Soit : $u_{n+1}-4=\frac{4+3 u_{n}-4^{2}}{\sqrt{4+3 u_{n}}+4}=\frac{3\left(u_{n}-4\right)}{u_{n+1}+4}$. À retenir ! L'usage de la quantité conjuguée qui permet d'éliminer les racines carrées gênantes d'un numérateur. Évidemment, les racines réapparaissent au dénominateur, mais leur capacité de nuisance est moindre... 8. Soit $Q_{n}$ la propriété $u_{n} \leq 4$.

Montrons par récurrence que, pour tout entier naturel $n, Q_{n}$ est vraie. Initialisation : On a : $u_{0}=1$. Donc $u_{0} \leq 4$. Donc $P_{0}$ est vraie. Hérédité : Soit $n$ un entier naturel, supposons que $P_{n}$ soit vraie. On a donc: $u_{n} \leq 4$, ce qui implique que $u_{n}-4 \leq 0$. On a vu que : $u_{n+1}-4=\frac{3\left(u_{n}-4\right)}{u_{n+1}+4}$.

Or, comme tous les termes de $\left(u_{n}\right)$ sont strictement positifs, on a : $u_{n+1}+4>4$. Donc : $u_{n+1}-4<\frac{3}{4}\left(u_{n}-4\right)$. Et comme $u_{n}-4 \leq 0$, on obtient : $u_{n+1}-4 \leq 0$. Et par là : $Q_{n+1}$ est vraie. Conclusion : pour tout naturel $n, u_{n} \leq 4$. 9. Finalement, la suite ( $u_{n}$ ) est strictement croissante et majorée (par 4). Donc elle est convergente. Et comme sa seule limite possible est 4, elle converge vers 4.