Cours : Orthogonalité et distances dans l'espace

Orthogonalité et distances dans l'espace

I Produit scalaire dans l'espace

Remarque : les définitions et propriétés relatives au produit scalaire de deux vecteurs du plan s'étendent à l'espace. En voici quelques-unes.

Définition

Soient $\vec{u}$ un vecteur, et A et B deux points tels que $\vec{u}=\overrightarrow{A B}$. La norme de $\vec{u}$ est la distance AB . Ainsi : $|\vec{u}|=A B$.

Voici la première formule à connaître.

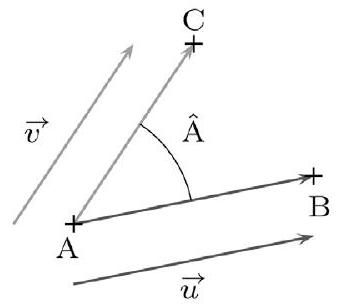
Définition Produit scalaire et angle

Soient $\vec{u}$ et $\vec{v}$ deux vecteurs. Le produit scalaire de $\vec{u}$ par $\vec{v}$, noté $\vec{u} \cdot \vec{v}$, est le nombre réel défini de la façon suivante : $-\operatorname{si} \vec{u}=\overrightarrow{0}$ ou si $\vec{v}=\overrightarrow{0}$, alors $\vec{u} \cdot \vec{v}=0$

• sinon, si $\mathrm{A}, \mathrm{B}$ et C sont trois points tels que $\vec{u}=\overrightarrow{A B}$ et $\vec{v}=\overrightarrow{A C}$, alors : $\vec{u} \cdot \vec{v}=|\vec{u}| \times|\vec{v}| \times \cos \hat{A}$ Cette dernière égalité s'écrit alors : $\overrightarrow{A B} \cdot \overrightarrow{A C}=A B \times A C \times \cos \hat{A}$

Norme et produit scalaire

Soient $\vec{u}$ un vecteur. On a alors: $|\vec{u}|^{2}=\vec{u} \cdot \vec{u}$

Propriétés

Soit $\vec{u}, \vec{v}$ et $\vec{w}$ trois vecteurs et $\lambda$ un réel. Propriété de symétrie : $\vec{u} \cdot \vec{v}=\vec{v} \cdot \vec{u}$. Propriétés de linéarité : $(\lambda \vec{u}) \cdot \vec{v}=\lambda \times(\vec{u} \cdot \vec{v}) \quad \vec{u} \cdot(\vec{v}+\vec{w})=\vec{u} \cdot \vec{v}+\vec{u} \cdot \vec{w}$

Voici le second type de formule à connaître.

Propriété Produit scalaire et projeté orthogonal

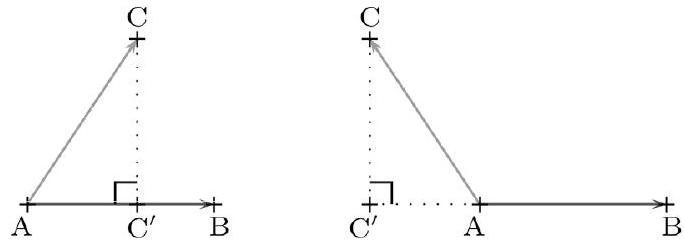
Si A et B sont deux points distincts, Si C'' est le projeté orthogonal de C sur (AB), alors : $\overrightarrow{A B} \cdot \overrightarrow{A C}=A B \times A C^{\prime} \quad$ si $\overrightarrow{A B}$ et $\overrightarrow{A C^{\prime}}$ ont même sens. $\overrightarrow{A B} \cdot \overrightarrow{A C}=-A B \times A C^{\prime} \quad$ si $\overrightarrow{A B}$ et $\overrightarrow{A C^{\prime}}$ sont de sens opposés. $\overrightarrow{A B} \cdot \overrightarrow{A C}=0 \quad$ si $\overrightarrow{A C^{\prime}}=\overrightarrow{0}$.

Voici le troisième type de formule à connaître.

Propriété Produit scalaire et normes

Soient $\vec{u}$ et $\vec{v}$ deux vecteurs. Voici les 3 identités de polarisation. $\vec{u} \cdot \vec{v}=\frac{1}{2}\left(|\vec{u}+\vec{v}|^{2}-|\vec{u}|^{2}-|\vec{v}|^{2}\right)$ $\vec{u} \cdot \vec{v}=\frac{1}{2}\left(|\vec{u}|^{2}+|\vec{v}|^{2}-|\vec{u}-\vec{v}|^{2}\right)$ $\vec{u} \cdot \vec{v}=\frac{1}{4}\left(|\vec{u}+\vec{v}|^{2}-|\vec{u}-\vec{v}|^{2}\right)$

Première application.

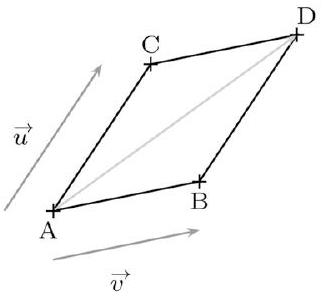
Si ABDC est un parallélogramme tel que $\vec{u}=\overrightarrow{A B}$ et $\vec{v}=\overrightarrow{A C}$, alors la première identité devient :

$$ \overrightarrow{A B} \cdot \overrightarrow{A C}=\frac{1}{2}\left(A D^{2}-A B^{2}-A C^{2}\right) $$

Seconde application.

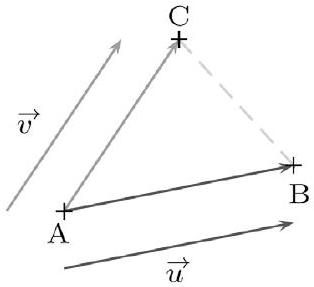
Si A, B et C sont trois points tels que $\vec{u}=\overrightarrow{A B}$ et $\vec{v}=\overrightarrow{A C}$, alors la seconde identité devient :

$$ \overrightarrow{A B} \cdot \overrightarrow{A C}=\frac{1}{2}\left(A B^{2}+A C^{2}-B C^{2}\right) $$

La première identité de polarisation permet de retrouver les autres. Mais mieux vaut les savoir toutes pour être plus efficace!

Définition

Deux vecteurs $\vec{u}$ et $\vec{v}$ sont orthogonaux si et seulement si $\vec{u} \cdot \vec{v}=0$.

Définition

Le repère ( $O, \vec{\imath}, \vec{\jmath}, \vec{k}$ ) ou la base ( $\vec{\imath}, \vec{\jmath}, \vec{k}$ ) est orthonormé si et seulement si les vecteurs $\vec{\imath}, \vec{\jmath}$ et $\vec{k}$ sont orthogonaux deux à deux et ont chacun pour norme 1 .

Voici le quatrième type de formule à connaître.

Propriété Produit scalaire et coordonnées

L'espace est muni d'une base orthonormée ( $\vec{\imath}, \vec{\jmath}, \vec{k}$ ).

Soit $\vec{u}(x ; y ; z)$ et $\vec{v}\left(x^{\prime} ; y^{\prime} ; z^{\prime}\right)$ deux vecteurs. alors : $\vec{u} \cdot \vec{v}=x x^{\prime}+y y^{\prime}+z z^{\prime}$

Propriétés

L'espace est muni d'une base orthonormée ( $\vec{\imath}, \vec{\jmath}, \vec{k}$ ). Si $\vec{u}$ a pour coordonnées ( $x ; y ; z$ ), alors $|\vec{u}|=\sqrt{x^{2}+y^{2}+z^{2}}$ L'espace est muni d'un repère orthonormé $O, \vec{\imath}, \vec{\jmath}, \vec{k}$ ). Soient $A\left(x_{A} ; y_{A} ; z_{A}\right)$ et $B\left(x_{B} ; y_{B} ; z_{B}\right)$ deux points, alors : $\quad A B=\sqrt{\left(x B-x_{A}\right)^{2}+\left(y B-y_{A}\right)^{2}+\left(z B-z_{A}\right)^{2}}$

Savoir faire

Le produit scalaire se calcule avec 4 types de formules : la première concerne distances et angles, la seconde le projeté orthogonal, la troisième les normes, et la dernière les coordonnées dans un repère orthonormé. Il faut choisir la formule adaptée à l'exercice !

II Orthogonalité dans l'espace

a. Droites orthogonales

Définition

Soit $d$ une droite de vecteur directeur $\vec{u}$. Soit $d^{\prime}$ une droite de vecteur directeur $\vec{v}$. $d$ et $d^{\prime}$ sont orthogonales si et seulement si $\vec{u} \cdot \vec{v}=0$.

Propriété

Soient $d$ et $d$ ' deux droites orthogonales. Si $d$ et $d^{\prime}$ ne sont pas coplanaires, alors elles ne sont pas sécantes. Si $d$ et $d$ ' sont coplanaires, alors elles se coupent selon un angle droit ; on dit qu'elles sont perpendiculaires.

b. Droites et plans orthogonaux

Définition et propriété

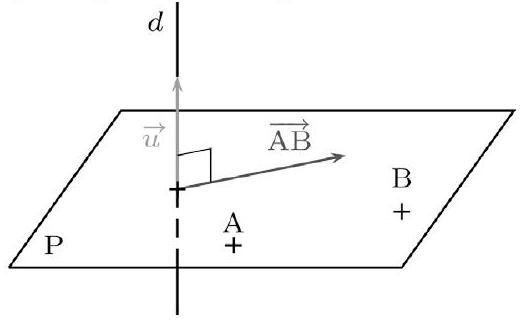
Soit $d$ une droite de vecteur directeur $\vec{u}$. Soit P un plan de vecteurs directeurs $\vec{v}$ et $\vec{w}$. $d$ et P sont orthogonaux si et seulement si $\vec{u} \cdot \vec{v}=0$ et $\vec{u} \cdot \vec{w}=0$. $d$ et P sont orthogonaux si et seulement si quels que soient les points A et B de P , on a $: \vec{u} \cdot \overrightarrow{A B}=0$.

Définition

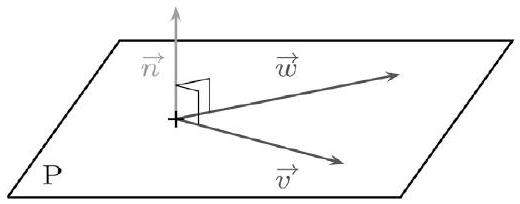
Soit $\vec{n}$ un vecteur non nul. Soit P un plan de vecteurs directeurs $\vec{v}$ et $\vec{w}$. Le vecteur $\vec{n}$ est normal au plan $P$ si et seulement si $\vec{n} \cdot \vec{v}=0$ et $\vec{n} \cdot \vec{w}=0$.

Propriété

Soit $d$ une droite de vecteur directeur $\vec{n}$. Soit P un plan. $d$ et P sont orthogonaux si et seulement si le vecteur $\vec{n}$ est normal au plan P .

Propriété

Soient $\vec{n}$ un vecteur non nul et A un point de l'espace. L'ensemble des points M de l'espace tels que $\overrightarrow{A M} \cdot \vec{n}=0$ est le plan P qui passe par A et admet $\vec{n}$ pour vecteur normal.

c. Projetés orthogonaux

Propriété

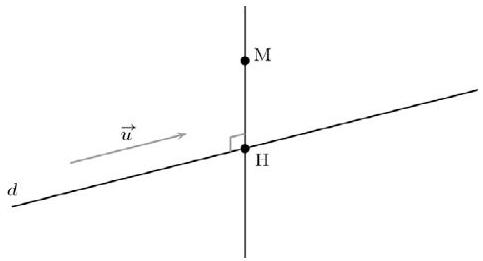
Soit M un point de l'espace. Soit $d$ une droite de vecteur directeur $\vec{u}$. Le projeté orthogonal du point M sur la droite $d$ est le point H si et seulement si H appartient à $d$ et les vecteurs $\vec{u}$ et $\overrightarrow{M H}$ sont orthogonaux.

Propriété

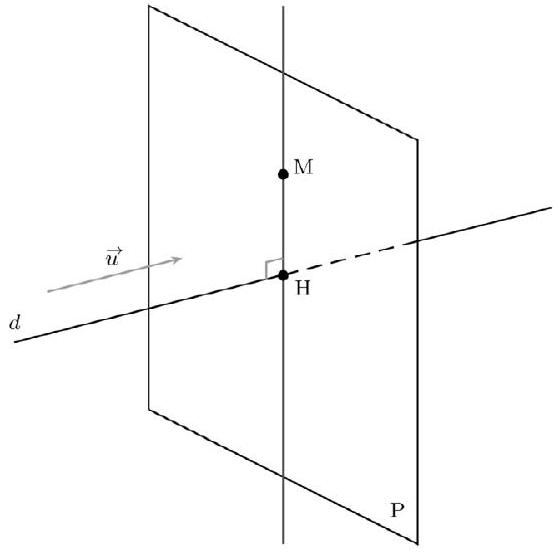
Soit M un point de l'espace. Soit $d$ une droite de vecteur directeur $\vec{u}$. Le projeté orthogonal du point M sur la droite $d$ est le point H si et seulement si H appartient à $d$ et au plan P passant par M et de vecteur normal $\vec{u}$.

Définition

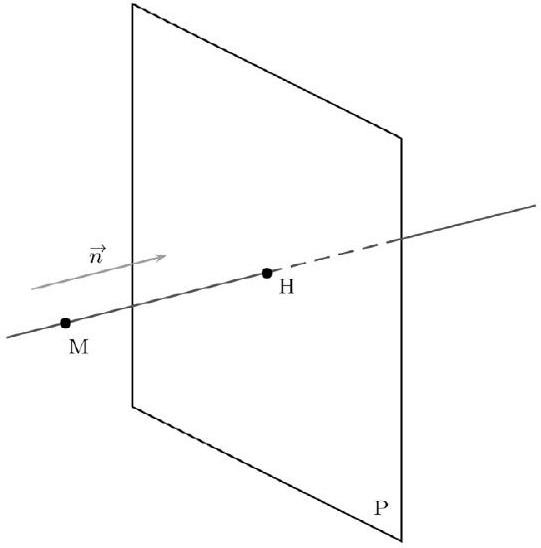
Soit M un point de l'espace. Soit $P$ un plan de vecteur normal $\vec{n}$. Le projeté orthogonal du point M sur le plan P est le point H si et seulement si H appartient à P et à la droite passant par M et de vecteur directeur $\vec{n}$.

Propriétés

Le projeté orthogonal d'un point M sur une droite $d$ est le point de $d$ le plus proche de M. Le projeté orthogonal d'un point M sur un plan P est le point de P le plus proche de M.

Définitions

La distance entre un point M et une droite $d$ est la distance entre M et son projeté orthogonal sur $d$. La distance entre un point $M$ et un plan $P$ est la distance entre $M$ et son projeté orthogonal sur P.

Savoir faire.

Quel est l'intérêt du produit scalaire dans l'espace? Il permet de déterminer l'angle entre 2 vecteurs, en particulier l'angle droit. Il permet de caractériser facilement les points d'un plan dont on connaît un point et un vecteur normal. Mais attention, la formule de calcul analytique du produit scalaire nécessite un repère orthonormal !