Exercices : Fonctions sinus et cosinus

Exercices corrigés

Exercice 1

1. Résoudre sur $\mathbb{R}$ l'équation (1): $2 \sin (3 x)-1=0$.
2. Résoudre sur $]-\pi ; \pi]$ l'équation (2) : $\cos ^{2}(2 x)-0,5=0$.
3. Résoudre sur $]-\pi ; \pi]$ l'inéquation (3) : $2 \sin x-\sqrt{3}<0$. 4.a. Montrer que $\frac{1}{2}$ est racine du trinôme $X^{2}+\left(\frac{\sqrt{3}-1}{2}\right) X-\frac{\sqrt{3}}{4}$. 4.b. Déterminer alors l'autre racine de ce trinôme. 4.c. Résoudre sur $]-\pi ; \pi]$ l'inéquation (4) : $\cos ^{2} x+\left(\frac{\sqrt{3}-1}{2}\right) \cos x \geq \frac{\sqrt{3}}{4}$.

Corrigé

La notation $a=b[x]$, où $x$ est un réel, est équivalente à : $a=b+k x$ où $k \in \mathbb{Z}$. $a=b[x]$ se dit «a égale $b$ modulo $x$ »

La résolution d'une équation trigonométrique utilise souvent :

• soit l'équivalence $\sin a=\sin b \Leftrightarrow a=b[2 \pi]$ ou $a=\pi-b[2 \pi]$,
• soit l'équivalence $\cos a=\cos b \Leftrightarrow a=b[2 \pi]$ ou $a=-b[2 \pi]$.

1. On résout sur $\mathbb{R}$. (1) $\Leftrightarrow 2 \sin (3 x)-1=0 \Leftrightarrow \sin (3 x)=\frac{1}{2} \Leftrightarrow \sin (3 x)=\sin \frac{\pi}{6}$.

Soit : (1) $\Leftrightarrow 3 x=\frac{\pi}{6}+2 k \pi \quad$ ou $\quad 3 x=\pi-\frac{\pi}{6}+2 k \pi \quad$ avec $k \in \mathbb{Z}$.

Soit : (1) $\Leftrightarrow x=\frac{\pi}{18}+k \frac{2 \pi}{3} \quad$ ou $\quad x=\frac{5 \pi}{18}+k \frac{2 \pi}{3} \quad$ avec $k \in \mathbb{Z}$. Donc $S_{1}=\left{\frac{\pi}{18}\left[\frac{2 \pi}{3}\right] ; \frac{5 \pi}{18}\left[\frac{2 \pi}{3}\right]\right}$. 2. On résout tout d'abord sur $\mathbb{R}$. (2) $\Leftrightarrow \cos ^{2}(2 x)=\frac{2}{4} \Leftrightarrow \cos (2 x)=\frac{\sqrt{2}}{2} \quad$ ou $\quad \cos (2 x)=-\frac{\sqrt{2}}{2}$.

Soit : $(2) \Leftrightarrow \cos (2 x)=\cos \frac{\pi}{4} \quad$ ou $\quad \cos (2 x)=\cos \left(\pi-\frac{\pi}{4}\right)$. Soit : $(2) \Leftrightarrow \cos (2 x)=\cos \frac{\pi}{4} \quad$ ou $\quad \cos (2 x)=\cos \left(\frac{3 \pi}{4}\right)$.

On résout tout d'abord la première équation : $\cos (2 x)=\cos \frac{\pi}{4} \quad$ (a). (a) $\Leftrightarrow 2 x=\frac{\pi}{4}+2 k \pi \quad$ ou $\quad 2 x=-\frac{\pi}{4}+2 k \pi \quad$ avec $k \in \mathbb{Z}$.

Soit : (a) $\Leftrightarrow x=\frac{\pi}{8}+k \pi \quad$ ou $\quad x=-\frac{\pi}{8}+k \pi \quad$ avec $k \in \mathbb{Z}$. Mais seules les solutions dans $]-\pi ; \pi]$ sont demandées. Il s'agit de : $\frac{\pi}{8}+0 \times \pi=\frac{\pi}{8}, \quad \frac{\pi}{8}-1 \times \pi=-\frac{7 \pi}{8}, \quad-\frac{\pi}{8}+0 \times \pi=-\frac{\pi}{8} \quad$ et $-\frac{\pi}{8}+1 \times \pi=\frac{7 \pi}{8}$.

On résout ensuite la seconde équation : $\cos (2 x)=\cos \frac{3 \pi}{4}$ (b) $\Leftrightarrow 2 x=\frac{3 \pi}{4}+2 k \pi \quad$ ou $\quad 2 x=-\frac{3 \pi}{4}+2 k \pi \quad$ avec $k \in \mathbb{Z}$.

Soit : (b) $\Leftrightarrow x=\frac{3 \pi}{8}+k \pi \quad$ ou $\quad x=-\frac{3 \pi}{8}+k \pi \quad$ avec $k \in \mathbb{Z}$. Mais seules les solutions dans ] - $\pi ; \pi]$ sont demandées. Il s'agit de : $\frac{3 \pi}{8}+0 \times \pi=\frac{3 \pi}{8}, \quad \frac{3 \pi}{8}-1 \times \pi=-\frac{5 \pi}{8}, \quad-\frac{3 \pi}{8}+0 \times \pi=-\frac{3 \pi}{8} \quad$ et $-\frac{3 \pi}{8}+1 \times \pi=\frac{5 \pi}{8}$.

Finalement, on obtient donc : $\mathrm{S}_{2}=\left{-\frac{7 \pi}{8} ;-\frac{5 \pi}{8} ;-\frac{3 \pi}{8} ;-\frac{\pi}{8} ; \frac{\pi}{8} ; \frac{3 \pi}{8} ; \frac{5 \pi}{8} ; \frac{7 \pi}{8}\right}$.

Autre méthode : (2) $\Leftrightarrow 2 \cos ^{2}(2 x)-1=0 \Leftrightarrow \cos (4 x)=0$.

Soit : $(2) \Leftrightarrow \cos (4 x)=\cos \frac{\pi}{2} \quad$ ou $\quad \cos (4 x)=\cos \left(-\frac{\pi}{2}\right)$. Soit : (2) $\Leftrightarrow 4 x=\frac{\pi}{2}+2 k \pi \quad$ ou $\quad 4 x=-\frac{\pi}{2}+2 k \pi \quad$ avec $k \in \mathbb{Z}$. Soit : (2) $\Leftrightarrow x=\frac{\pi}{8}+k \frac{\pi}{2} \quad$ ou $\quad x=-\frac{\pi}{8}+k \frac{\pi}{2} \quad$ avec $k \in \mathbb{Z}$. On retrouve alors les mêmes solutions dans $]-\pi ; \pi]$ qu'avec la première méthode.

La résolution d'une inéquation trigonométrique nécessite souvent la résolution de l'équation trigonométrique associée, puis d'un raisonnement reposant sur le cercle trigonométrique. 3. (3) $\Leftrightarrow 2 \sin x-\sqrt{3}<0 \Leftrightarrow \sin x<\frac{\sqrt{3}}{2}$.

On résout l'équation trigonométrique associée. $\sin x=\frac{\sqrt{3}}{2} \Leftrightarrow \sin x=\sin \frac{\pi}{3} \Leftrightarrow x=\frac{\pi}{3}[2 \pi]$ ou $x=\pi-\frac{\pi}{3}[2 \pi]$. Donc, sur $]-\pi ; \pi]$, on a : $\sin (x)=\frac{\sqrt{3}}{2} \Leftrightarrow x=\frac{\pi}{3}$ ou $x=\frac{2 \pi}{3}$.

On revient alors à l'inéquation. Par lecture du cercle trigonométrique, on obtient : (3) $\Leftrightarrow-\pi<x<\frac{\pi}{3} \quad$ ou $\quad \frac{2 \pi}{3}<x \leq \pi$.

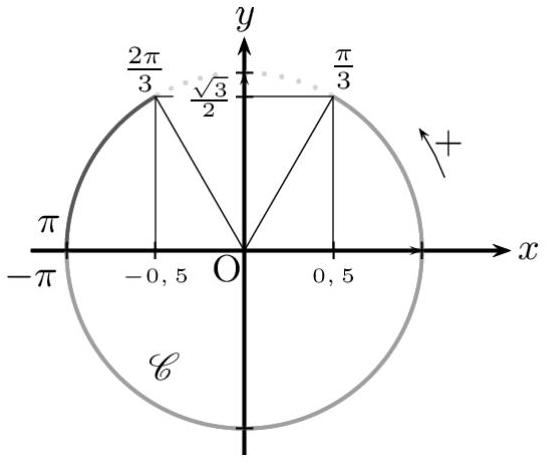
Donc $\left.\left.\mathrm{S}_{3}=\right]-\pi ; \frac{\pi}{3}[\cup] \frac{2 \pi}{3} ; \pi\right]$. 4.a. On calcule : $\left(\frac{1}{2}\right)^{2}+\left(\frac{\sqrt{3}-1}{2}\right)\left(\frac{1}{2}\right)-\frac{\sqrt{3}}{4}=\frac{1}{4}+\frac{\sqrt{3}-1}{4}-\frac{\sqrt{3}}{4}=0$.

Donc $\frac{1}{2}$ est racine du trinôme $X^{2}+\left(\frac{\sqrt{3}-1}{2}\right) X-\frac{\sqrt{3}}{4}$. 4.b. On rappelle que, si le trinôme $a x^{2}+b x+c$ admet pour racines réelles (éventuellement doubles) $x_{1}$ et $x_{2}$, alors il se factorise sous la forme : $a\left(x-x_{1}\right)\left(x-x_{2}\right)$. Or ici, le trinôme a au moins une racine réelle. Il est donc factorisable sous cette forme, et on a, pour tout $X$ réel, l'égalité : $X^{2}+\left(\frac{\sqrt{3}-1}{2}\right) X-\frac{\sqrt{3}}{4}=1\left(X-x_{1}\right)\left(X-\frac{1}{2}\right)$.

On développe le membre de gauche. On obtient alors l'égalité, vérifiée pour tout $X$ réel : $X^{2}+\left(\frac{\sqrt{3}-1}{2}\right) X-\frac{\sqrt{3}}{4}=X^{2}+\left(-x_{1}-\frac{1}{2}\right) X+\frac{x_{1}}{2}$. Par identification, on obtient alors : $1=1 \quad$ et $\quad \frac{\sqrt{3}-1}{2}=-x_{1}-\frac{1}{2} \quad$ et $\quad-\frac{\sqrt{3}}{4}=\frac{x_{1}}{2}$. D'où : $-\frac{\sqrt{3}}{2}=x_{1}$ dans les deux dernières équations (ce qui est rassurant). La seconde racine du trinôme est donc $-\frac{\sqrt{3}}{2}$. 4.c. (4) $\Leftrightarrow \cos ^{2} x+\left(\frac{\sqrt{3}-1}{2}\right) \cos x-\frac{\sqrt{3}}{4} \geq 0$

On pose alors : $X=\cos x$, et on résout : $X^{2}+\left(\frac{\sqrt{3}-1}{2}\right) X-\frac{\sqrt{3}}{4} \geq 0$. Le membre de gauche est le trinôme précédent, qui a 2 racines : $-\frac{\sqrt{3}}{2}$ et $\frac{1}{2}$, et dont le coefficient dominant vaut 1 . Comme le coefficient dominant du trinôme est positif, ce trinôme est positif ou nul à l'extérieur de ses racines, et par là, sur $\left.]-\infty ;-\frac{\sqrt{3}}{2}\right] \cup\left[\frac{1}{2} ;+\infty[\right.$. On a donc : $X^{2}+\left(\frac{\sqrt{3}-1}{2}\right) X-\frac{\sqrt{3}}{4} \geq 0 \Leftrightarrow X \leq-\frac{\sqrt{3}}{2}$ ou $X \geq \frac{1}{2}$.

Or, comme on avait posé $X=\cos x$, on revient alors à l'inéquation d'origine, et on obtient: (4) $\Leftrightarrow \cos x \leq-\frac{\sqrt{3}}{2}$ ou $\cos x \geq \frac{1}{2}$.

Soit (a) l'inéquation $\cos x \leq-\frac{\sqrt{3}}{2}$ et (b) l'inéquation $\cos x \geq \frac{1}{2}$.

On résout l'équation trigonométrique associée à (a). $\cos x=-\frac{\sqrt{3}}{2} \Leftrightarrow \cos x=\cos \left(\pi-\frac{\pi}{6}\right) \Leftrightarrow \cos x=\cos \left(\frac{5 \pi}{6}\right)$. Soit : $\cos x=-\frac{\sqrt{3}}{2} \Leftrightarrow x=\frac{5 \pi}{6}[2 \pi] \quad$ ou $\quad x=-\frac{5 \pi}{6}[2 \pi]$. Et comme on raisonne sur $]-\pi ; \pi]$, on obtient : $\quad x=\frac{5 \pi}{6} \quad$ ou $\quad x=-\frac{5 \pi}{6}$. On revient alors à l'inéquation (a) : $\cos x \leq-\frac{\sqrt{3}}{2}$. Par lecture du cercle trigonométrique, on obtient : (a) $\Leftrightarrow-\pi<x \leq-\frac{5 \pi}{6} \quad$ ou $\quad \frac{5 \pi}{6} \leq x \leq \pi$.

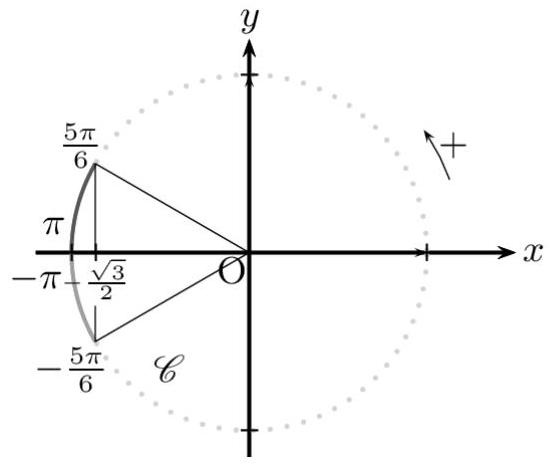
On résout l'équation trigonométrique associée à (b). $\cos x=\frac{1}{2} \Leftrightarrow \cos x=\cos \left(\frac{\pi}{3}\right)$. Soit : $\cos x=\frac{1}{2} \Leftrightarrow x=\frac{\pi}{3}[2 \pi] \quad$ ou $\quad x=-\frac{\pi}{3}[2 \pi]$. Et comme on raisonne sur ] $-\pi ; \pi]$, on obtient : $\quad x=\frac{\pi}{3} \quad$ ou $\quad x=-\frac{\pi}{3}$. On revient alors à l'inéquation (b) : $\cos x \geq \frac{1}{2}$. Par lecture du cercle trigonométrique, on obtient : (b) $\Leftrightarrow-\frac{\pi}{3} \leq x \leq \frac{\pi}{3}$.

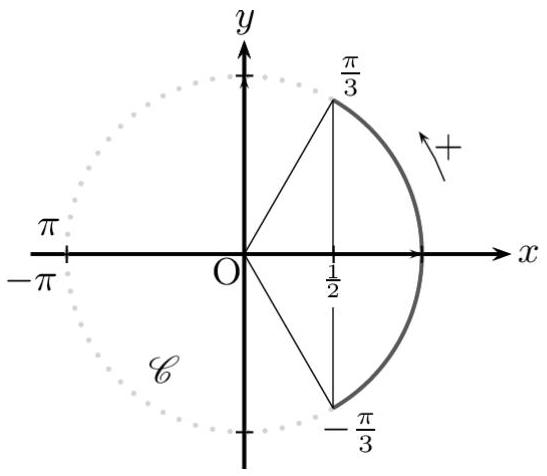
Finalement : $\left.\left.\mathrm{S}_{4}=\right]-\pi ;-\frac{5 \pi}{6}\right] \cup\left[-\frac{\pi}{3} ; \frac{\pi}{3}\right] \cup\left[\frac{5 \pi}{6} ; \pi\right]$.

Exercice 2

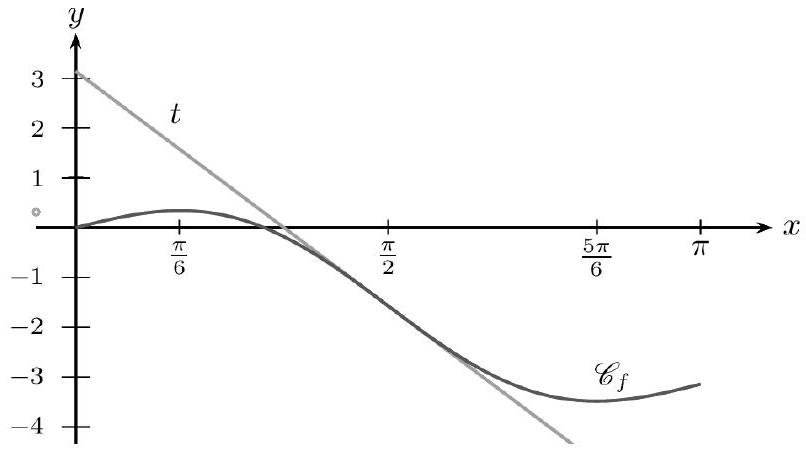
Soit $f$ définie sur $[0 ; \pi]$ par $f(x)=\sin (2 x)-x$. Soit $\mathrm{C}_{f}$ sa courbe représentative.

1. Déterminer la valeur exacte de $f(0), f\left(\frac{\pi}{6}\right), f\left(\frac{5 \pi}{6}\right)$ et $f(\pi)$. 2.a. Montrer que $f^{\prime}(x)=2 \times \cos (2 x)-1$ 2.b. On admet que, pour tout $x$, on a : $\cos (2 x)=2 \cos ^{2} x-1$.

Montrer que $f^{\prime}(x)=4 \cos ^{2} x-3$. 3.a. Résoudre l'inéquation : $4 X^{2}-3 \geq 0$. 3.b. Résoudre sur $[0 ; \pi]$ l'inéquation $4 \cos ^{2} x-3 \geq 0$, puis déterminer le sens de variation de $f$ sur $[0 ; \pi]$. 4. Retrouvons le sens de variation de $f$ sur $[0 ; \pi]$ par une autre méthode (non exigible). Résoudre sur $[0 ; \pi]$ l'inéquation $2 \times \cos (2 x)-1 \geq 0$, puis retrouver le sens de variation de $f$ sur $[0 ; \pi]$. 5. Déterminer une équation de la tangente $t$ à $C_{f}$ en $\frac{\pi}{2}$. 6. Représenter graphiquement $\mathrm{C}_{f}$ et $t$.

Corrigé

1. $f(0)=0$. $f\left(\frac{\pi}{6}\right)=\sin \left(\frac{\pi}{3}\right)-\frac{\pi}{6}=\frac{\sqrt{3}}{2}-\frac{\pi}{6}$. $f\left(\frac{5 \pi}{6}\right)=\sin \left(\frac{5 \pi}{3}\right)-\frac{5 \pi}{6}=\sin \left(-\frac{\pi}{3}\right)-\frac{5 \pi}{6}=-\frac{\sqrt{3}}{2}-\frac{5 \pi}{6}$. $f(\pi)=\sin (2 \pi)-\pi=-\pi$. 2.a. On pose $f=g(2 x+0)-x$ avec $g(y)=\sin y$.

Donc $f^{\prime}=2 g^{\prime}(2 x+0)-1$ avec $g^{\prime}(y)=\cos y$. Et par là : $f^{\prime}(x)=2 \times \cos (2 x)-1$. 2.b. On a : $f^{\prime}(x)=2 \times \cos (2 x)-1$.

Or : $\cos (2 x)=2 \cos ^{2} x-1$. Donc $f^{\prime}(x)=2\left(2 \cos ^{2} x-1\right)-1=4 \cos ^{2} x-2-1$. Soit : $f^{\prime}(x)=4 \cos ^{2} x-3$. 3.a. On a: $4 X^{2}-3 \geq 0 \Leftrightarrow X^{2} \geq \frac{3}{4} \Leftrightarrow X \leq-\frac{\sqrt{3}}{2}$ ou $X \geq \frac{\sqrt{3}}{2}$. 3.b. On résout sur $[0 ; \pi]$ l'inéquation : $4 \cos ^{2} x-3 \geq 0$ (1).

Or, si on pose $X=\cos x$, l'inéquation devient : $4 X^{2}-3 \geq 0$. Et cette inéquation a été résolue au 2.b. Par conséquent : (1) $\Leftrightarrow \cos x \leq-\frac{\sqrt{3}}{2}$ ou $\cos x \geq \frac{\sqrt{3}}{2}$.

On résout les équations trigonométriques associées. $\cos x=-\frac{\sqrt{3}}{2} \Leftrightarrow \cos x=\cos \left(\pi-\frac{\pi}{6}\right)=\cos \frac{5 \pi}{6}$. Soit : $\cos x=-\frac{\sqrt{3}}{2} \Leftrightarrow x=\frac{5 \pi}{6}+2 k \pi(k \in \mathbb{Z})$ ou $x=-\frac{5 \pi}{6}+2 k^{\prime} \pi(k \in \mathbb{Z})$. Soit : $\cos x=-\frac{\sqrt{3}}{2} \Leftrightarrow x=\frac{5 \pi}{6}[2 \pi]$ ou $x=-\frac{5 \pi}{6}[2 \pi]$. Donc, sur $[0 ; \pi]$, on a : $\cos x=-\frac{\sqrt{3}}{2} \Leftrightarrow x=\frac{5 \pi}{6}$.

On revient alors à l'inéquation $\cos x \leq-\frac{\sqrt{3}}{2}$. Par lecture du cercle trigonométrique, on obtient : $\cos x \leq-\frac{\sqrt{3}}{2} \Leftrightarrow \frac{5 \pi}{6}<x \leq \pi$ (on rappelle que $x$ est cherché dans $[0 ; \pi]$ ) Cela correspond à l'arc de gauche ci-dessous.

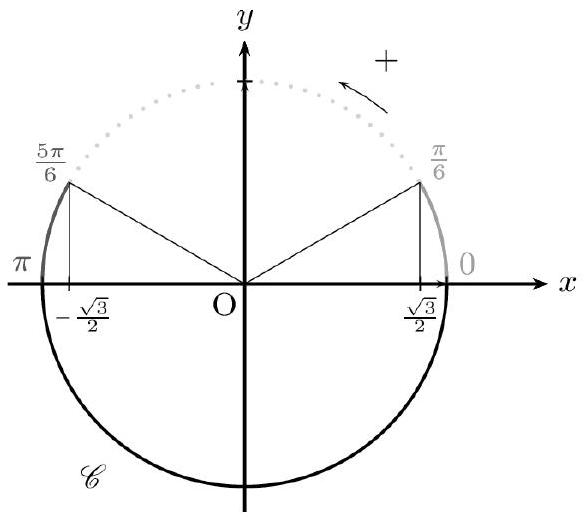
On procède de même avec la seconde inéquation. $\cos x=\frac{\sqrt{3}}{2} \Leftrightarrow \cos x=\cos \left(\frac{\pi}{6}\right) \Leftrightarrow x=\frac{\pi}{6}[2 \pi]$ ou $x=-\frac{\pi}{6}[2 \pi]$. Donc, sur $[0 ; \pi]$, on $a: \cos x=\frac{\sqrt{3}}{2} \Leftrightarrow x=\frac{\pi}{6}$.

On revient alors à l'inéquation $\cos x \geq \frac{\sqrt{3}}{2}$. Par lecture du cercle trigonométrique, on obtient : $\cos x \geq \frac{\sqrt{3}}{2} \Leftrightarrow 0 \leq x \leq \frac{\pi}{6}$ (on rappelle que $x$ est cherché dans $[0 ; \pi]$ ). Cela correspond à l'arc de droite ci-dessus.

On vient de trouver pour quels $x$ la dérivée $f^{\prime}(x)$ est positive. $D$ 'où le tableau de signes de $f^{\prime}$ et le tableau de variation de $f$ :

$x$	$0 \frac{\pi}{6} \quad \frac{5 \pi}{6} \quad+\pi$
$f^{\prime}(x)$	+ 0 - 0 +
$f(x)$	$\int^{\frac{\sqrt{3}}{2}-\frac{\pi}{6}}-\frac{\sqrt{3}}{2}-\frac{5 \pi}{6}$

4. On résout sur $[0 ; \pi]$ l'inéquation : $2 \times \cos (2 x)-1 \geq 0$ (2).

On $a:(2) \Leftrightarrow \cos (2 x) \geq \frac{1}{2}$. On résout l'équation trigonométrique associée. $\cos (2 x)=\frac{1}{2} \Leftrightarrow \cos (2 x)=\cos \left(\frac{\pi}{3}\right)$. Soit : $\cos (2 x)=\frac{1}{2} \Leftrightarrow \Leftrightarrow 2 x=\frac{\pi}{3}+2 k \pi(k \in \mathbb{Z})$ ou $2 x=-\frac{\pi}{3}+2 k^{\prime} \pi\left(k^{\prime} \in \mathbb{Z}\right)$. Soit : $\cos (2 x)=\frac{1}{2} \Leftrightarrow x=\frac{\pi}{6}+k \pi(k \in \mathbb{Z})$ ou $x=-\frac{\pi}{6}+k^{\prime} \pi\left(k^{\prime} \in \mathbb{Z}\right)$. Donc, sur $[0 ; \pi]$, on a : $\cos (2 x)=\frac{1}{2} \Leftrightarrow x=\frac{\pi}{6}$ ou $x=\frac{5 \pi}{6}$. On revient alors à l'inéquation (2) : $\cos (2 x) \geq \frac{1}{2}$. On résout sur $[0 ; \pi]$. Les intervalles à examiner sont donc : $\left[0 ; \frac{\pi}{6}\right],\left[\frac{\pi}{6} ; \frac{5 \pi}{6}\right]$ et $\left[\frac{5 \pi}{6} ; \pi\right]$. Or, par lecture du cercle trigonométrique, on obtient : $0 \leq x \leq \frac{\pi}{6} \Rightarrow 0 \leq 2 x \leq \frac{\pi}{3} \Rightarrow \cos (2 x) \geq \frac{1}{2}$. $\frac{\pi}{6} \leq x \leq \frac{5 \pi}{6} \Rightarrow \frac{\pi}{3} \leq 2 x \leq \frac{5 \pi}{3} \Rightarrow \cos (2 x) \leq \frac{1}{2}$. $\frac{5 \pi}{6} \leq x \leq \pi \Rightarrow \frac{5 \pi}{3} \leq 2 x \leq 2 \pi \Rightarrow \cos (2 x) \geq \frac{1}{2}$.

On vient donc de trouver pour quels $x$ la dérivée $f^{\prime}(x)$ est positive. $D$ 'où le tableau de signes de $f$ ' et le tableau de variation de $f$ :

$x$	0	$\frac{\pi}{6}$	$\frac{5 \pi}{6}$	$+\pi$
$f^{\prime}(x)$	+	0	-	0	+
		$\frac{\sqrt{3}}{2}-\frac{\pi}{6}$
$f(x)$
	0			$-\frac{\sqrt{3}}{2}-\frac{5 \pi}{6}$

5. $f\left(\frac{\pi}{2}\right)=\sin \pi-\frac{\pi}{2}=-\frac{\pi}{2}$. $f^{\prime}\left(\frac{\pi}{2}\right)=4 \cos ^{2}\left(\frac{\pi}{2}\right)-3=-3$. Donc $t$ admet pour équation : $y=-\frac{\pi}{2}+(-3)\left(x-\frac{\pi}{2}\right)$. Soit : $y=-3 x+\pi$.

6. Voici les tracés demandés :

Exercice 3

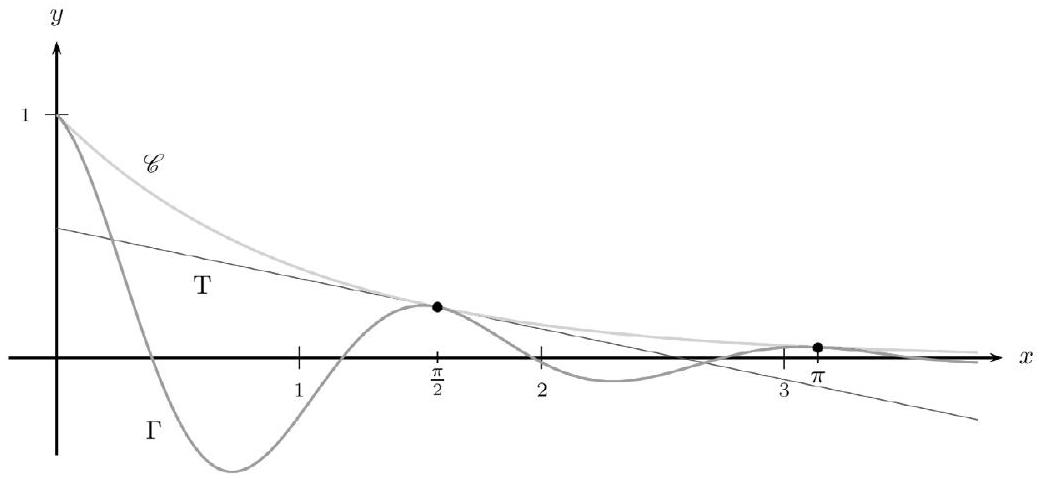
Cet exercice utilise les cours sur les suites, la fonction exponentielle, les limites et la dérivation. Soit la fonction $f$ définie sur $\left[0 ;+\infty\left[\right.\right.$ par : $f(x)=e^{-x} \cos (4 x)$ et $\Gamma$ sa courbe représentative tracée un repère orthonormé ci-dessous. On considère également la fonction $g$ définie sur $\left[0 ;+\infty\left[\right.\right.$ par $g(x)=e^{-x}$ et on nomme $C$ sa courbe représentative dans le même repère orthonormé . 1.a. Montrer que, pour tout réel $x$ appartenant à l'intervalle $[0 ;+\infty[$, $-e^{-x} \leq f(x) \leq e^{-x}$. 1.b. En déduire la limite de $f$ en $+\infty$. 2. Déterminer les coordonnées des points communs aux courbes $\Gamma$ et $C$. 3.a. On définit la suite $\left(u_{n}\right) \operatorname{sur} \mathbb{N}$ par $u_{n}=f\left(n \frac{\pi}{2}\right)$.

Montrer que la suite ( $u_{n}$ ) est une suite géométrique. En préciser la raison. 3.b. En déduire le sens de variation de la suite ( $u_{n}$ ) et étudier sa convergence. 4.a. Montrer que, pour tout réel $x$ appartenant à l'intervalle $[0 ;+\infty[$, $f^{\prime}(x)=-e^{-x}[\cos (4 x)+4 \sin (4 x)]$. 4.b. En déduire que les courbes $\Gamma$ et $C$ ont même tangente en chacun de leurs points communs. 5. Donner une valeur approchée à $10^{-1}$ près par excès du coefficient directeur de la droite $T$ tangente à la courbe $\Gamma$ au point d'abscisse $\frac{\pi}{2}$. Compléter le graphique en y $\operatorname{traçant} T$ et $C$.

Corrigé

1.a. Soit $x$ un réel. On a : $-1 \leq \cos (4 x) \leq 1$.

Et comme $e^{-x}>0$, on obtient: $-e^{-x} \leq e^{-x} \cos (4 x) \leq e^{-x}$. Soit : $-e^{-x} \leq f(x) \leq e^{-x}$. c'est vrai pour tout $x$, et donc en particulier sur $[0 ;+\infty[$. 1.b. On a vu que, pour tout réel $x$ de $\left[0 ;+\infty\left[\right.\right.$, on a : $-e^{-x} \leq f(x) \leq e^{-x}$.

Or, comme $\lim _{x \rightarrow+\infty}-x=-\infty$ et $\lim _{y \rightarrow-\infty} e^{y}=0$, on obtient : $\lim _{x \rightarrow+\infty} e^{-x}=0$. Et par là: $\lim _{x \rightarrow+\infty}-e^{-x}=-0=0$. Donc, les membres de droite et de gauche ont tous les deux la même limite (nulle) en $+\infty$.

Donc, d'après le théorème des gendarmes, on obtient : $\lim {x \rightarrow+\infty} f(x)=0$. 2. Pour trouver les abscisses des points communs aux courbes $\Gamma$ et $C$, il suffit de résoudre l'équation $f(x)=g(x)$ sur $[0 ;+\infty[$. $f(x)=g(x) \Leftrightarrow e^{-x} \cos (4 x)=e^{-x} \Leftrightarrow \cos (4 x)=1$ (on peut diviser chacun des membres de l'égalité par $e^{-x}$ qui est non nul). Donc : $f(x)=g(x) \Leftrightarrow 4 x=k 2 \pi$ (avec $k$ entier naturel) (et non pas relatif car $x$ est positif ou nul). Donc : $f(x)=g(x) \Leftrightarrow x=k \frac{\pi}{2}$ (avec $k$ entier naturel) $\Leftrightarrow x=0\left[\frac{\pi}{2}\right]$. Donc, sur $\left[0 ;+\infty\left[, \Gamma\right.\right.$ et $C$ se coupent aux points d'abscisses $k \frac{\pi}{2}$, lorsque $k$ décrit l'ensemble des entiers naturels. Ces points ont pour ordonnées respectives: $f\left(k \frac{\pi}{2}\right)=e^{-k \frac{\pi}{2}} \cos \left(4 \times k \frac{\pi}{2}\right)=e^{-k \frac{\pi}{2}} \cos (k \times 2 \pi)=e^{-k \frac{\pi}{2}} \times 1=e^{-k \frac{\pi}{2}}=\left(e^{-\frac{\pi}{2}}\right)^{k}$ Finalement, les points cherchés ont pour coordonnées $\left(k \frac{\pi}{2} ;\left(e^{-\frac{\pi}{2}}\right)^{k}\right)$, pour $k$ dans $\mathbb{N}$. 3.a. Chacun aura remarqué que les $u{n}$ sont les ordonnées des points de contact précédents.

Donc, pour tout $n$ dans $\mathbb{N}$, on a : $u_{n}=\left(e^{-\frac{\pi}{2}}\right)^{n}$. Donc la suite ( $u_{n}$ ) est une suite géométrique de raison $e^{-\frac{\pi}{2}}$, et de premier terme 1 . 3.b. Il est clair que $0<e^{-\frac{\pi}{2}}$.

Par ailleurs, comme $-\frac{\pi}{2}<0$, on a : : $e^{-\frac{\pi}{2}}<e^{0}$ (par stricte croissance de l'exponentielle). Et donc : $e^{-\frac{\pi}{2}}<1$. Finalement, la raison de la suite géométrique $\left(e^{-\frac{\pi}{2}}\right)^{n}$ est strictement entre 0 et 1 , et par là, cette suite est strictement décroissante et admet pour limite $\mathbf{0}$. 4.a. Soit $x$ appartenant à l'intervalle $[0 ;+\infty[$.

On pose $u=e^{-x}$ et $v=\cos (4 x)$. On obtient alors $u^{\prime}=-e^{-x}$ (la dérivée de $e^{u}$ estu' $e^{u}$ ). On obtient également $v^{\prime}=4 \times(-\sin (4 x)=-4 \sin (4 x)$ (la dérivée de $g(a x+b)$ est $\left.a g^{\prime}(a x+b)\right)$. Ici, $f=u v$, et donc $f^{\prime}=u^{\prime} v+u v^{\prime}$. Soit : $f^{\prime}(x)=-e^{-x} \times \cos (4 x)+e^{-x} \times(-4 \sin (4 x))=-e^{-x}[\cos (4 x)+4 \sin (4 x)]$. 4.b. Pour montrer que les deux courbes ont même tangente en chacun de leurs points communs, il suffit de montrer qu'elles y ont le même nombre dérivé. Il est inutile de déterminer les équations des tangentes car ces tangentes passent nécessairement par les points communs. Or, un point commun à $\Gamma$ et $C$ admet une abscisse du type $k \frac{\pi}{2}$, avec $k$ entier naturel. On calcule alors : $f^{\prime}\left(k \frac{\pi}{2}\right)=-e^{-k \frac{\pi}{2}}\left[\cos \left(4 \times k \frac{\pi}{2}\right)+4 \sin \left(4 \times k \frac{\pi}{2}\right)\right]=-e^{-k \frac{\pi}{2}}[1+0]=-e^{-k \frac{\pi}{2}}$. Par ailleurs, il est clair que $g^{\prime}(x)=-e^{-x}$ pour tout $x$ de $[0 ;+\infty[$, et donc : $g^{\prime}\left(k \frac{\pi}{2}\right)=-e^{-k \frac{\pi}{2}}$. Donc : $f^{\prime}\left(k \frac{\pi}{2}\right)=g^{\prime}\left(k \frac{\pi}{2}\right)$, et c'est vrai pour tout naturel $k$. Donc les deux courbes ont même tangente en chacun de leurs points communs. On note que le coefficient directeur de la tangente en $k \frac{\pi}{2}$ vaut $-u_{k}$, ce qui est curieux, mais c'est tout! 5. On a : $f^{\prime}\left(\frac{\pi}{2}\right)=-e^{-\frac{\pi}{2}}\left[\cos \left(4 \times \frac{\pi}{2}\right)+4 \sin \left(4 \times \frac{\pi}{2}\right)\right]$.

Soit : $f^{\prime}\left(\frac{\pi}{2}\right)=-e^{-\frac{\pi}{2}}[\cos (2 \times \pi)+4 \sin (2 \times \pi)]=-e^{-\frac{\pi}{2}}[1+0]=-e^{-\frac{\pi}{2}}$. Donc : $f^{\prime}\left(\frac{\pi}{2}\right) \approx-0,2$. C'est une valeur approchée à $10^{-1}$ près par excès du coefficient directeur de la droite $T$ tangente à la courbe $\Gamma$ au point d'abscisse $\frac{\pi}{2}$. Le graphique est complété ci-dessous en y traçant $\Gamma$ et $C$ grâce à quelques points obtenus à la calculatrice, et $T$ grâce à son coefficient directeur.

Exercice 4

Cet exercice utilise les cours sur les limites, la continuité et la dérivation. Soit la fonction $\tan$ définie sur $\left[0 ; \frac{\pi}{2}\left[\right.\right.$ par $: \tan x=\frac{\sin x}{\cos x}$ et $\Gamma$ sa courbe représentative dans un repère orthonormé. On considère également la fonction $g$ définie sur $] 0 ;+\infty\left[\right.$ par $g(x)=\frac{3 x}{x^{2}+5}$ et on nomme $C$ sa courbe représentative dans un autre repère orthonormé . On considère également la fonction $f$ définie sur $] 0 ;+\infty\left[\right.$ par $f(x)=x+\frac{5}{x}$ et on nomme $C$ sa courbe représentative dans un autre repère orthonormé .

1. Montrer que la fonction $\tan$ admet le tableau de variation suivant :

$x$	0
$\tan ^{\prime}(x)$	+
$\tan (x)$

2.a. Pour quelle valeur de $x$ la fonction $f$ atteint-elle son minimum ? 2.b. Montrer que $g$ atteint son maximum lorsque $f$ atteint son minimum. 3.a. Soit $a$ un réel strictement positif. Montrer que l'équation $\tan x=g(a)$ admet une solution unique $x_{0}$ sur $\left[0 ; \frac{\pi}{2}[\right.$. 3.b. Pour quelle valeur de $a$ la solution $x_{0}$ est-elle maximale ?

Corrigé

1. On a : $\tan x=\frac{\sin x}{\cos x}$.

On pose $u=\sin x$ et $v=\cos x$. Donc $u^{\prime}=\cos x$ et $v^{\prime}=-\sin x$. Ici $\tan =\frac{u}{v}$ et donc $\tan ^{\prime}=\frac{u^{\prime} v-u v^{\prime}}{v^{2}}$. Donc $\tan ^{\prime}(x)=\frac{\cos x \times \cos x-\sin x \times(-\sin x)}{(\cos x)^{2}}$. Soit : $\tan ^{\prime}(x)=\frac{\cos ^{2} x+\sin ^{2} x}{\cos ^{2} x}$. Soit : $\tan ^{\prime}(x)=\frac{1}{\cos ^{2} x}$. $\tan ^{\prime}(x)$ est donc un quotient. Le numérateur, 1 , est strictement positif. Le dénominateur est un carré, et donc il est positif. Il est même strictement positif car $x$ est dans $\left[0 ; \frac{\pi}{2}[\right.$. Donc $\tan ^{\prime} x$ reste strictement positive sur $\left[0 ; \frac{\pi}{2}[\right.$. Donc la fonction tan est strictement croissante sur $\left[0 ; \frac{\pi}{2}[\right.$. Par ailleurs, $\tan 0=\frac{0}{1}=0$. Il reste à prouver que $\lim _{x \rightarrow \frac{\pi}{2}-} \tan x=+\infty$. On a: $\lim _{x \rightarrow \frac{\pi}{2}-} \sin x=0^{+}$et $\lim _{x \rightarrow \frac{\pi}{2}-} \cos x=\cos 0=1$ et $1>0$. Donc: $\lim _{x \rightarrow \frac{\pi}{2}}-\tan x=+\infty$ (limite d'un quotient). Finalement tan admet effectivement le tableau de variation suivant :

$x$	0
$\tan ^{\prime}(x)$	+
$\tan (x)$

2.a. On a: $f(x)=x+\frac{5}{x}=x+5 \times \frac{1}{x}$.

Donc : $f^{\prime}(x)=1+5 \times\left(\frac{-1}{x^{2}}\right)=\frac{x^{2}-5}{x^{2}}=\frac{(x-\sqrt{5})(x+\sqrt{5})}{x^{2}}$.

Or, sur $] 0 ;+\infty\left[\right.$, on a : $x+\sqrt{5}>0$ et $x^{2}>0$, et par là, $f^{\prime}(x)$ est du signe de $x-\sqrt{5}$. D'où le tableau donnant le sens de variation de $f$ :

$x$	0		$\sqrt{5}$
$f^{\prime}(x)$		-	0	$+\infty$
$f(x)$

La fonction $f$ admet un minimum pour $x=\sqrt{5}$. 2.b. On a : $g(x)=\frac{3 x}{x^{2}+5}=\frac{3}{\frac{x^{2}+5}{x}}=\frac{3}{x+\frac{5}{x}}=\frac{3}{f(x)}=3 \times \frac{1}{f(x)}$.

Donc : $g^{\prime}(x)=3 \times \frac{-f^{\prime}(x)}{(f(x))^{2}}$. Comme 3 et le dénominateur $(f(x))^{2}$ sont strictement positifs, $g^{\prime}(x)$ est du signe de $-f^{\prime}(x)$. Et par là, $g$ varie en sens contraire de $f$. Donc $g$ atteint son maximum lorsque $f$ atteint son minimum. 3.a. Notons tout d'abord que, pour tout nombre $a$ de $] 0 ;+\infty[$, on a : $g(a)>0(\operatorname{car} g(a)$ est un quotient de termes strictement positifs). D'après le tableau de variation de tan du 1., la fonction tan est continue et strictement croissante sur $\left[0 ; \frac{\pi}{2}[\right.$. Or $g(a)$ est strictement supérieur à $\tan 0=0$, et $\lim {x \rightarrow \frac{\pi}{2}-} \tan (x)=+\infty$. Donc, d'après le théorème de la bijection, l'équation $\tan (x)=g(a)$ admet une unique solution $x{0}$ sur $\left[0 ; \frac{\pi}{2}[\right.$. 3.b. Comme tan est strictement croissante $\left[0 ; \frac{\pi}{2}\left[\right.\right.$, la solution $x_{0}$ est maximale lorsque $\tan x_{0}$ est maximale. Et comme $\tan \left(x_{0}\right)=g(a)$, cela se produit lorsque $g(a)$ est maximale. Et donc, d'après le 2., la solution $x_{0}$ est maximale pour $a=\sqrt{5}$.