Passer au contenu principal

Fiche Exercices N 1 : Intégrale d'une fonction

Exercice 1:

Aire sous une courbe - intégrale

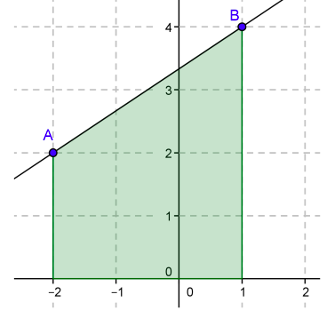
On considère la fonction affine $f$ dont la courbe ci-contre passe par les points A et B.

2025-11-19-12.40.40.png

  1. Déterminer l’expression de $f(x)$.

  2. En déduire une primitive $F$ de $f$.

  3. a) Déterminer l’intégrale $\int_{-2}^1 f(x) dx$ à l’aide de $F$.

    En déduire l’aire du domaine vert.

    b) Déterminer l’aire du domaine vert d’une autre façon.

Exercice 2:

Aire sous une courbe - aire d'un triangle, trapèze, demi-cercle

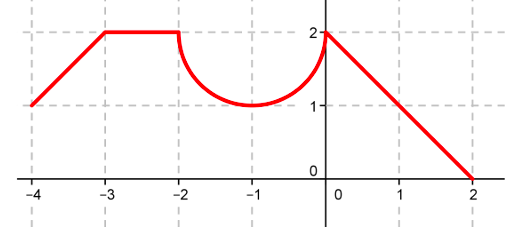
On a tracé la courbe d’une fonction $f$ définie sur $[-4; 2]$.
Sur $[-2; 0]$, la courbe est un demi-cercle.

2025-11-19-12.40.55.png

  1. Déterminer $\int_{-4}^{-2} f(x) dx$, puis $\int_{-2}^0 f(x) dx$, puis $\int_0^2 f(x) dx$
  2. En déduire $\int_{-4}^2 f(x) dx$

Exercice 3:

Calcul d'intégrale à l'aide de primitive - intégrale d'un polynôme - $x^n$

Calculer les intégrales suivantes:

a) $\int_{-1}^2 2x^5-x^2-1{\rm d}x$

b) $\int_{0}^{-1} (1-t^2)(2+3t){\rm d}t$

c) $\int_{2}^{5} \dfrac 23{\rm d}x$

d) $\int_{-1}^3 \dfrac1n{\rm d}x$

Exercice 4:

Calcul d'intégrale à l'aide de primitive - intégrale d'un quotient - $\frac{u'}{u}$

Calculer les intégrales suivantes:

a) $\int_{0}^1 \dfrac{1}{1+2x}~{\rm d}x$

b) $\int_{1}^e \dfrac{6x^2+4x-1}{x}{\rm d}x$

c) $\int_{0}^1 \dfrac{x^2}{1+x^3}{\rm d}x$

d) $\int_{1}^4 \dfrac1{3t}-\dfrac3{t^2}{\rm d}t$

Exercice 5:

intégrale avec des exponentielles ou des racines - $u'e^u$ - $\dfrac{u'}{\sqrt{u}}$

Calculer les intégrales suivantes:

a) $\int_{0}^1 e^{-x}+\dfrac 6{e^{2x}}~{\rm d}x$

b) $\int_{-1}^2 xe^{-x^2}~{\rm d}x$

c) $\int_{0}^4 \dfrac 3 {\sqrt{2x+1}}~{\rm d}x$

Exercice 6:

Calcul d'intégrale à l'aide de primitive - intégrale d'un quotient de polynômes

  1. Etudier, suivant les valeurs du réel $x$, le signe de $x^2+2x+5$.
  2. En déduire la valeur de $\int_{-2}^1 \dfrac{x+1}{x^2+2x+5}{\rm d}x$.

Exercice 7:

*Aire entre 2 courbes - intégrale

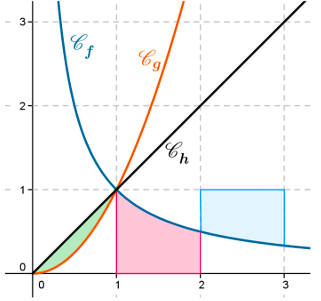
On a tracé la courbe de la fonction $f$ définie sur $[0; +\infty[$ par $f(x) = \dfrac{1}{x}$.
On a tracé également les courbes des fonctions $g$ et $h$ définies sur $[0; +\infty[$ par $g(x) = x^2$ et $h(x) = x$.

2025-11-19-12.41.18.png

  1. Déterminer l’aire du domaine rose.
  2. Déterminer l’aire du domaine bleu.
  3. Déterminer l’aire du domaine vert.

Exercice 8:

Intégrale et aire sous une courbe d'une fonction changeant de signe - aire sous une parabole

La courbe $\mathcal{C}$ représente dans un repère orthogonal, la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=x^2-2x-3$. Les unités graphiques sont: 1 cm sur l'axe des abscisses et 0.5 cm sur l'axe des ordonnées.

2025-11-19-12.41.46.png

  1. Etudier la position relative de la courbe $\mathcal{C}$ par rapport à l'axe des abscisses.
  2. En déduire l'aire $\mathcal{A}$ du domaine en unité d'aire puis en cm² compris entre la courbe $\mathcal{C}$, l'axe des abscisses et les droites d'équation $x=-2$ et $x=3$.

Exercice 9:

Intégrale et aire entre deux courbes - position relative de $2$ courbes

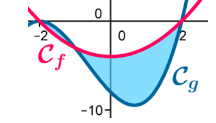
$\mathcal{C}_f$ et $\mathcal{C}_g$ sont les courbes représentatives de deux fonctions $f$ et $g$ définies sur $\mathbb{R}$ par $f(x)=x^2-4$ et $g(x)=(x+2)^2(x-2)$.

2025-11-19-12.42.02.png

  1. Etudier la position relative de leurs courbes représentatives.
  2. En déduire l'aire $\mathcal{A}$ du domaine en unité d'aire compris entre les deux courbes sur l'intervalle $[-2;2]$.

Exercice 10:

Primitive sous la forme $(ax+b)e^(-x)$

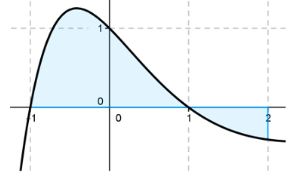
On considère la fonction définie sur $\mathbb{R}$ par $f(x)=(1-x^2)e^{-x}$ dont on a tracé la courbe ci-contre:

2025-11-19-12.42.13.png

  1. Déterminer les réels $a$, $b$ et $c$ tels que la fonction définie sur $\mathbb{R}$ par ${\rm F}(x)=(ax^2+bx+c)e^{-x}$ soit une primitive de $f$.
  2. En déduire l'aire de la surface bleue.

Exercice 11:

Variations de la primitive $F$ à partir des variations de $f$

On donne ci-dessous le tableau de variations d'une fonction $f$ définie sur $\mathbb{R}$:

On définit la fonction $F$ sur $\mathbb{R}$ par $F(x)=\int_{1}^x f(t) {\rm d}t$.

  1. Déterminer le tableau de variations de F.
  2. Déterminer le signe de l'intégrale $\int_{1}^3 f(t){\rm d}t$ et de $\int_{1}^{-5} f(t) {\rm d}t$.
  3. Déterminer la limite de F en $+\infty$ et en $-\infty$.

Exercice 12:

Signe d'une intégrale

On considère la fonction $f$ définie sur $\mathbb{R}$ par $f(x)=\dfrac{e^{-4x}}{1+e^{-4x}}$. Pour tout réel $x$, on pose ${\rm I}(x)=\int_{3}^{x} f(t) , \mathrm{d}t$. Déterminer le signe de ${\rm I}(x)$ en fonction de $x$, en justifiant.

Exercice 13:

Intégrale - Aire finie ou infinie ?

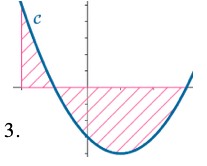
En voyant cette courbe représentative d'une fonction:

  • Ali affirme que : "Si la fonction représentée tend vers 0 en $+\infty$ alors l'aire hachurée sous la courbe sur $[1;+\infty[$ est finie".
  • Antoine lui répond: "Même si cette fonction tend vers 0 en $+\infty$, la longueur de l'intervalle $[1;+\infty[$ étant infinie, l'aire hachurée ne peut pas être finie".

A l'aide de deux exemples, justifier qu'ils ont tort tous les deux.

Exercice 15:

Encadrer une intégrale - comparer $2$ intégrales

On a tracé ci-dessous la courbe d’une fonction $f$ définie sur $\mathbb{R}$.

  1. Comparer les intégrales $\int_{0}^{1} f(x) dx$ et $\int_{1}^{2} f(x) dx$.
  2. Comparer les intégrales $\int_{-2}^{0} f(x) dx$ et $\int_{0}^{2} f(x) dx$.
  3. Encadrer l’intégrale $\int_{-1}^{2} f(x) dx$.

Exercice 16:

Encadrer une intégrale - aire

On a tracé ci-dessous la courbe d’une fonction $f$ définie sur $\mathbb{R}$.

Déterminer un encadrement de l’intégrale $\int_{1}^{4} f(x) dx$.

Exercice 17:

Fonction définie par une intégrale

On considère la fonction définie sur $\mathbb{R}$ par $g(x) = \int_{1}^{x} \frac{1}{1+t^2} dt$.

  1. Justifier que $g$ est bien définie sur $\mathbb{R}$.
  2. Déterminer le tableau de variations de $g$.
  3. Déterminer le tableau de signe de $g(x)$.
  4. Démontrer que pour tout $x \geq 1$, $g(x) \leq 1$.
  5. Démontrer que l'inégalité du 4) reste vraie pour $x \leq 1$.

Exercice 18:

QCM intégrale

$f$ est une fonction continue sur $\mathbb{R}$.
Dire si les affirmations suivantes sont vraies ou fausses en justifiant :

a) $\int_{2}^{-1} f(x) dx = - \int_{1}^{-2} f(x) dx$

b) Si $\int_{0}^{1} f(x) dx = \int_{0}^{1} g(x) dx$ alors pour tout $x \in [0;1]$, $f(x) = g(x)$.

c) Si $\int_{-1}^{1} f(x) dx = 0$ alors pour tout $x \in [-1;1]$, $f(x) = 0$.

d) Si $f$ est positive sur $[2;3]$ alors $\int_{2}^{3} f(x) dx \geq 0$.

e) Si $\int_{2}^{3} f(x) dx \geq 0$ alors pour tout $x \in [2;3]$, $f(x) \geq 0$.

f) $\int_{2}^{3} f'(x) dx = F(3) - F(2)$ où $F = f^2$.

Exercice 19:

QCM fonction définie par une intégrale

Soit $f$ une fonction définie sur l’intervalle $[-2;5]$ et $F$ une primitive de $f$. On a tracé la courbe de $F$ ci-contre :

  1. Déterminer le tableau de signe de la fonction $f$ sur l’intervalle $[-2;5]$ .
  2. Déterminer la valeur $\int_{1}^3 f(x)~{\rm d}x$.

Exercice 20:

Encadrer une intégrale

  1. Démontrer que pour tout $x\ge 1$, $\dfrac 1{2x}\le \dfrac 1{x+\sqrt x}\le \dfrac 1{2\sqrt x}$.
  2. En déduire un encadrement de l'intégrale $\int_{2}^3 \dfrac{1}{x+\sqrt x}~{\rm d}x$.

Exercice 21:

Encadrer une intégrale - Encadrer $ln2$ - inégalité et intégrale

  1. Démontrer que pour tout réel $t\ge 1$, $\dfrac 1{t^2}\le \dfrac 1t\le \dfrac 1 {\sqrt t}$.
  2. En déduire que pour tout réel $x\ge 1$, $1-\dfrac 1x \le \ln x \le 2\sqrt x-2$.
  3. En déduire un encadrement de $\ln 2$. Vérifier la cohérence du résultat à l'aide d'une calculatrice.

Exercice 22:

Encadrer une intégrale - Encadrer $ln2$

  1. Démontrer que pour tout réel $t\ge 0$, $:1-t\le \dfrac 1{1+t}\le 1-t+t^2$.
  2. En déduire que pour tout réel $x\ge 0$, $:x-\dfrac {x^2}2 \le \ln (1+x) \le x-\dfrac {x^2}2+\dfrac{x^3}3$.
  3. En déduire un encadrement de $\ln 2$. Vérifier la cohérence du résultat à l'aide d'une calculatrice.

Exercice 23:

Suite définie par une intégrale

Pour tout entier naturel $n$, on pose $u_n = \int_{0}^{n} \dfrac{1}{1+x^2} dx$.

  1. Démontrer que la suite $(u_n)$ est croissante.
  2. Justifier que pour tout entier $n \geq 1$, $u_n \leq \int_{0}^{1} \dfrac{1}{1+x^2} dx + \int_{1}^{n} \dfrac{1}{x^2} dx$.
  3. Démontrer que $\int_{0}^{1} \dfrac{1}{1+x^2} dx \leq 1$.
  4. En déduire que la suite $(u_n)$ est convergente.

Exercice 24:

Aire entre $2$ courbes - $\dfrac{\ln x}{x}$ et $\dfrac{(\ln x)^2}{x}$

On se place dans un repère orthogonal d’unité $2$ cm sur l’axe des abscisses et 4 cm sur l’axe des ordonnées.
On a tracé les courbes de 2 fonctions $f$ et $g$ définies sur $]0; +\infty[$ par $f(x) = \dfrac{\ln x}{x}$ et $g(x) = \dfrac{(\ln x)^2}{x}$.

  1. Associer à chaque fonction la courbe qui lui correspond. Justifier.

  2. Déterminer graphiquement les positions relatives des courbes de $f$ et $g$ .

  3. Déterminer les positions relatives des courbes de $f$ et $g$ par le calcul. Comparer avec le résultat trouvé graphiquement.

  4. a) Déterminer graphiquement un majorant de l'aire du domaine vert en unité d'aire.

    b) Déterminer une primitive de $f$

    c) Déterminer une primitive de $g$.

    d) Déterminer l'aire du domaine vert en unité d'aire puis en $cm^2$ par le calcul.

    e) Comparer avec le résultat trouvé graphiquement.

Aucun commentaire à afficher

Retour en haut