Exercices : Vecteurs, droites et plans de l'espace

Exercices corrigés

Exercice 1

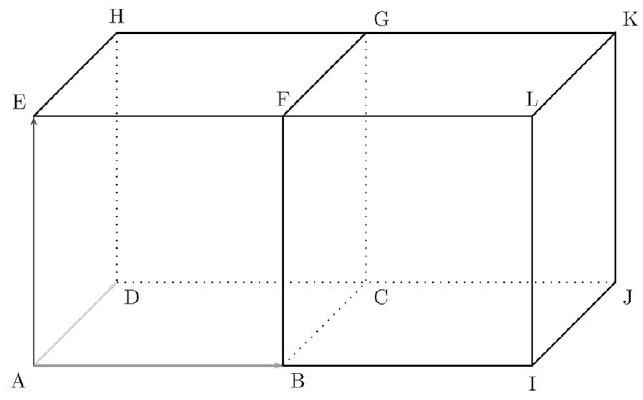
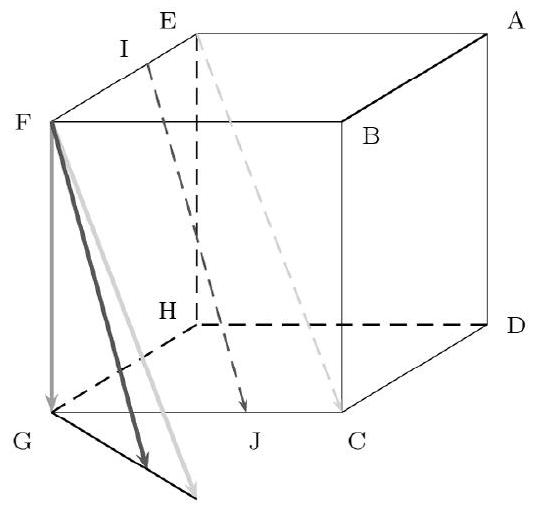
Aucune justification n'est demandée dans cet exercice. ABCDEFGH et BIJCFLKG sont deux cubes de même taille disposés côte à côte . Reproduire la figure donnée ci-après.

1. Construire le vecteur $\overrightarrow{A X}=2 \overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A E}$.

Où est le point X ? 2. Construire le vecteur $\overrightarrow{I Y}=-2 \overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A E}$.

Où est le point Y ? 3. Écrire le vecteur $\overrightarrow{I G}$ comme combinaison linéaire des vecteurs $\overrightarrow{A B}, \overrightarrow{A D}$ et $\overrightarrow{A E}$. Faire apparaître la combinaison sur le dessin. 4. Écrire le vecteur $\overrightarrow{C E}$ comme combinaison linéaire des vecteurs $\overrightarrow{A B}, \overrightarrow{A D}$ et $\overrightarrow{A E}$. Faire apparaître la combinaison sur le dessin.

Corrigé

Les justifications ci-dessous ne sont pas exigibles dans cet exercice. On rappelle que, pour construire une somme de vecteurs, il suffit de les mettre à la queue leu leu. 1.

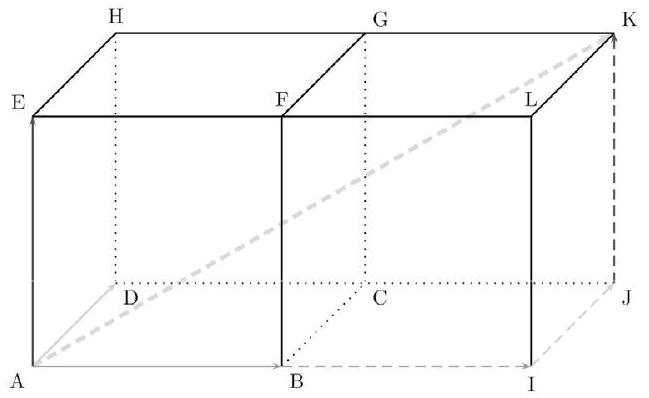
On a : $\overrightarrow{A X}=2 \overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A E}$. Or, vu les hypothèses, il est clair que : $\overrightarrow{A B}=\overrightarrow{B I}, \overrightarrow{A D}=\overrightarrow{I J}$ et $\overrightarrow{A E}=\overrightarrow{J K}$. Donc on obtient : $\overrightarrow{A X}=\overrightarrow{A B}+\overrightarrow{B I}+\overrightarrow{I J}+\overrightarrow{J K}$. Soit : $\overrightarrow{A X}=\overrightarrow{A K}$ (d'après la relation de Chasles). Et par là, le point $\mathbf{X}$ est en $\mathbf{K}$. À retenir! L'usage de la relation de Chasles pour simplifier une somme de vecteurs. 2.

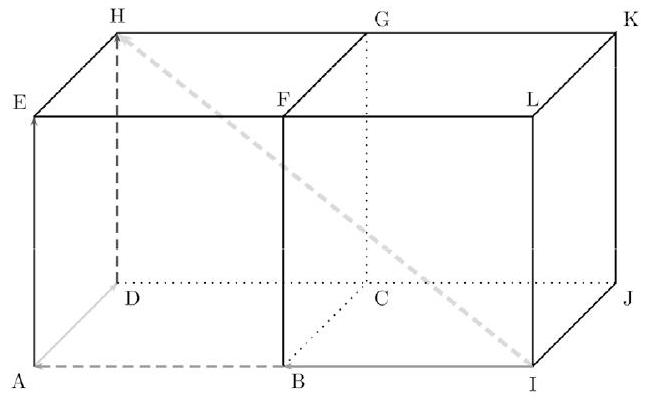
On raisonne commme précédemment. On a: $\overrightarrow{I Y}=-2 \overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A E}$. Donc, vu les hypothèses, il est clair que : $\overrightarrow{I Y}=\overrightarrow{I B}+\overrightarrow{B A}+\overrightarrow{A D}+\overrightarrow{D H}$. Soit : $\overrightarrow{I Y}=\overrightarrow{I H}$ (d'après la relation de Chasles).

Et par là, le point $\mathbf{Y}$ est en $\mathbf{H}$.

À retenir ! L'usage de la relation de Chasles pour simplifier une somme de vecteurs. 3. Cette fois-ci, la relation de Chasles permet de décomposer un vecteur en une somme.

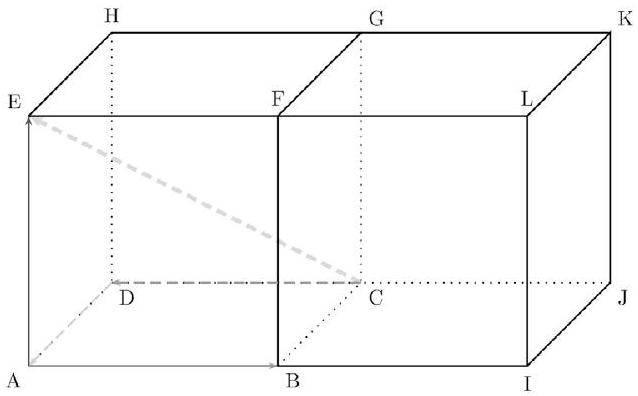
On a : $\overrightarrow{I G}=\overrightarrow{I B}+\overrightarrow{B C}+\overrightarrow{C G}$ (d'après la relation de Chasles). Soit: $\overrightarrow{I G}=-\overrightarrow{A B}+\overrightarrow{A D}+\overrightarrow{A E}$ (vu les hypothèses). 4. À nouveau, la relation de Chasles permet de décomposer un vecteur en une somme.

On a : $\overrightarrow{C E}=\overrightarrow{C D}+\overrightarrow{D A}+\overrightarrow{A E}$ (d'après la relation de Chasles). Soit: $\overrightarrow{C E}=-\overrightarrow{A B}-\overrightarrow{A D}+\overrightarrow{A E}$ (vu les hypothèses).

Exercice 2

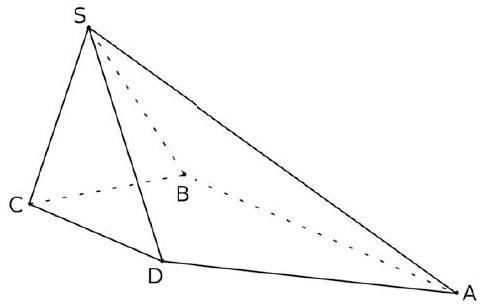
ABCDS est une pyramide non aplatie telle que, d'une part : les droites $(\mathrm{AB})$ et $(\mathrm{CD})$ sont parallèles, d'autre part: les droites $(\mathrm{CB})$ et $(\mathrm{DA})$ ne sont pas parallèles.

1. $\overrightarrow{B A}$ et $\overrightarrow{B S}$ ne sont pas colinéaires. Pourquoi?

Il est alors évident que $\overrightarrow{B A}$ et $\overrightarrow{B S}$ sont donc 2 vecteurs directeurs du plan ( ABC ). 2. Expliquer pourquoi $\overrightarrow{B A}$ et $\overrightarrow{C S}$ sont 2 vecteurs directeurs du plan (SCD). 3. Les plans $(\mathrm{SBA})$ et $(\mathrm{SCD})$ ne sont pas strictement parallèles. Pourquoi ? Les plans (SBA) et (SCD) sont sécants. Pourquoi? 4. a. De quelle nature est l'intersection des plans (SBA) et (SCD) ? b. Soit $d_{1}$ cette intersection. Donner un point de $d_{1}$. c. Déterminer un vecteur directeur de $d_{1}$. d. Reproduire le dessin et dessiner l'intersection $d_{1}$ des plans (SBA) et (SCD). 5. On admettra que les plans $(\mathrm{SBC})$ et $(\mathrm{SAD})$ sont sécants. a. Soit $d_{2}$ cette intersection. Donner un point évident de $d_{2}$. b. Pourquoi les droites $(\mathrm{CB})$ et $(\mathrm{DA})$ sont-elles sécantes? c. Soit F leur point d'intersection.

Pourquoi F est-il sur $d_{2}$ ? d. Reproduire le dessin et dessiner l'intersection $d_{2}$ des plans (SBC) et (SAD).

Corrigé

1. Les points $\mathrm{A}, \mathrm{B}$ et S sont non alignés (sinon la pyramide serait aplatie).

Donc $\overrightarrow{B A}$ et $\overrightarrow{B S}$ ne sont pas colinéaires. 2. Il est clair que $\overrightarrow{C D}$ et $\overrightarrow{C S}$ sont 2 vecteurs directeurs du plan (SCD).

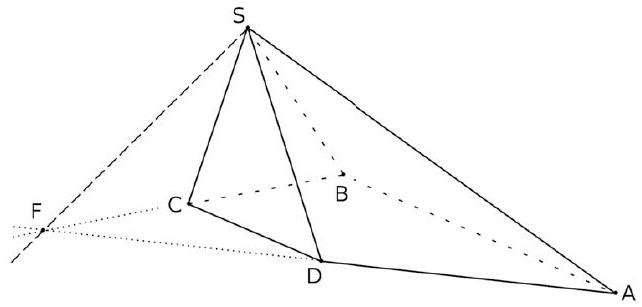
Donc $\overrightarrow{C D}$ et $\overrightarrow{C S}$ ne sont pas colinéaires et ils appartiennent à la direction de (SCD). Or, comme les droites (AB) et (CD) sont parallèles, les vecteurs $\overrightarrow{B A}$ et $\overrightarrow{C D}$ sont colinéaires (et non nuls). Donc $\overrightarrow{B A}$ et $\overrightarrow{C S}$ ne sont pas colinéaires et ils appartiennent à la direction de (SCD). Donc $\overrightarrow{B A}$ et $\overrightarrow{C S}$ sont également $\mathbf{2}$ vecteurs directeurs du plan (SCD). 3. Les plans ( SBA ) et ( SCD ) ont un point commun, le point S . Donc, ils ne sont pas strictement parallèles. Et par là, soit ils sont confondus, soit ils sont sécants. Ils ne sont pas confondus en un plan P , car ce plan P contiendrait les points $\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}$ et S , et la pyramide ABCDS serait aplatie. Donc les plans (SBA) et (SCD) sont sécants. 4. a. Les plans (SBA) et (SCD) sont sécants selon une droite $d_{1}$. b. Le point $S$ appartenant aux 2 plans est donc sur leur intersection $d_{1}$. c. Le vecteur $\overrightarrow{B A}$ fait partie des vecteurs directeurs des plans (SBA) et (SCD), et donc $\overrightarrow{B A}$ est vecteur directeur de leur intersection $d_{1}$. d. Finalement, $d_{1}$ est la droite passant par S de vecteur directeur $\overrightarrow{B A}$.

On constate qu'elle est parallèle à ( AB ) et à ( CD ) (ce résultat résulte de l'application du théorème du toit, hors programme). Elle est représentée en rouge dans le dessin ci-dessous. 5. a. Les plans (SBC) et (SAD) sont sécants selon une droite $d_{2}$ qui passe par le point S (car S appartient aux deux plans). Reste à déterminer un second point de cette droite $d_{2}$ pour la tracer. b. Les droites $(\mathrm{CB})$ et $(\mathrm{DA})$ ne sont pas parallèles. Or elles sont toutes deux dans le plan ( ABC ). Par conséquent elles sont sécantes. c. Soit F le point d'intersection des droites ( CB ) et ( DA ).

Comme F est sur (CB), il appartient au plan (SBC). Comme F est sur (DA), il appartient au plan (SAD). Donc F appartient aux deux plans $(\mathrm{SBC})$ et $(\mathrm{SAD})$, et par là, $\mathbf{F}$ appartient à leur intersection, c'est-à-dire à la droite $d_{2}$. d. Finalement, la droite $d_{2}$ passe donc par $S$ et par $F$.

Exercice 3

ABCDEFGH est un cube de côté non nul. Les points I et J vérifient $\overrightarrow{E I}=\frac{1}{3} \overrightarrow{E F}$ et $\overrightarrow{G J}=\frac{2}{3} \overrightarrow{G C}$.

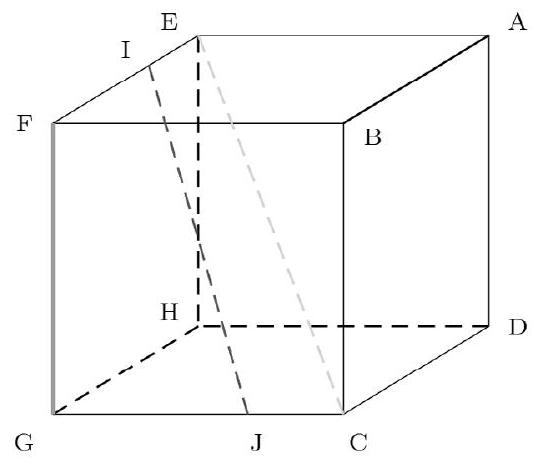
1. Montrer que les points $\mathrm{F}, \mathrm{G}, \mathrm{I}, \mathrm{J}, \mathrm{E}$ et C ne sont pas coplanaires.

Peut-on en déduire que les les vecteurs $\overrightarrow{F G}, \overrightarrow{I J}$ et $\overrightarrow{E C}$ ne sont pas coplanaires ?

On va montrer ci-après que les vecteurs $\overrightarrow{F G}, \overrightarrow{I J}$ et $\overrightarrow{E C}$ sont en réalité coplanaires, et ce par trois méthodes différentes. Il est vivement conseillé de connaître la relation de Chasles pour espérer répondre aux questions qui suivent... 2. Voici la Méthode 1. a. Montrer que $: \overrightarrow{I J}=\frac{2}{3}(\overrightarrow{E F}+\overrightarrow{G C})+\overrightarrow{F G}$. b. En déduire que $: \overrightarrow{I J}=\frac{2}{3} \overrightarrow{E B}+\overrightarrow{F G}$. c. Montrer finalement que $: \overrightarrow{I J}=\frac{2}{3} \overrightarrow{E C}+\frac{1}{3} \overrightarrow{F G}$. d. Conclure.

3. Voici la Méthode 2.

Ne pas utiliser ici ce qui a été prouvé dans le 2. Nous allons le démontrer autrement. Comme ABCDEFGH est un cube de côté non nul, ( $\overrightarrow{G C}, \overrightarrow{G H}, \overrightarrow{G F}$ ) constitue une base de l'espace. a. Décomposer le vecteur $\overrightarrow{E C}$ dans la base ( $\overrightarrow{G C}, \overrightarrow{G H}, \overrightarrow{G F}$ ). b. Décomposer le vecteur $\overrightarrow{I J}$ dans la base ( $\overrightarrow{G C}, \overrightarrow{G H}, \overrightarrow{G F}$ ). c. Soit $a$ et $b$ deux réels.

On considère alors le vecteur $a \cdot \overrightarrow{E C}+b \cdot \overrightarrow{I J}$. Montrer que : $\quad a \cdot \overrightarrow{E C}+b \cdot \overrightarrow{I J}=\overrightarrow{F G} \Leftrightarrow a=-2$ et $b=3$. d. Conclure.

4. Voici la Méthode 3.

Ne pas utiliser ici ce qui a été prouvé dans le 2. ou le 1. Nous allons le démontrer autrement. Cette méthode est une revisite de la méthode 2. Comme ABCDEFGH est un cube de côté non nul, ( $G, \overrightarrow{G C}, \overrightarrow{G H}, \overrightarrow{G F}$ ) constitue un repère de l'espace. a. Donner (sans justifier) les coordonnées des points $\mathrm{F}, \mathrm{G}, \mathrm{I}, \mathrm{J}, \mathrm{E}$ et C dans ce repère. b. Donner (sans justifier) les coordonnées des vecteurs $\overrightarrow{E C}, \overrightarrow{I J}$ et $\overrightarrow{F G}$ dans ce repère. c. Déterminer les réels $a$ et $b$ tels que $a \cdot \overrightarrow{E C}+b \cdot \overrightarrow{I J}=\overrightarrow{F G}$. d. Conclure.

Corrigé

1. Si les points $\mathrm{F}, \mathrm{G}, \mathrm{I}, \mathrm{J}, \mathrm{E}$ et C étaient coplanaires, alors E appartiendrait au plan ( $\mathrm{F}, \mathrm{G}, \mathrm{C}$ ), et le cube serait aplati, ce qui est absurde. Donc ces points ne sont pas coplanaires. On ne peut rien conclure quant à la coplanérité des vecteurs $\overrightarrow{F G}, \overrightarrow{I J}$ et $\overrightarrow{E C}$. Par contre, si les points avaient été coplanaires, alors les 3 vecteurs $\overrightarrow{F G}, \overrightarrow{I J}$ et $\overrightarrow{E C}$, construits sur ces points, auraient été nécessairement coplanaires.

Dans ce qui suit, l'astuce est de décomposer les vecteurs à l'aide de la relation de Chasles. Pour l'appliquer avec efficacité, il est conseillé de «suivre» les traits de construction, ce qui permettra une utilisation efficace des hypothèses données dans l'énoncé.

2. Méthode 1.

Préambule. ABCDEFGH est un cube, et par là : $\overrightarrow{G C}=\overrightarrow{F B} \quad$ (1) $\quad$ et $\quad \overrightarrow{B C}=\overrightarrow{F G} \quad$ (2). Par ailleurs, on a: $\quad \overrightarrow{E I}=\frac{1}{3} \overrightarrow{E F}$ Enfin, comme : $\overrightarrow{G J}=\frac{2}{3} \overrightarrow{G C}$, on a : $\quad \overrightarrow{J C}=\frac{1}{3} \overrightarrow{G C}$ 2.a. On a : $\overrightarrow{I J}=\overrightarrow{I F}+\overrightarrow{F G}+\overrightarrow{G J} \quad$ (Chasles).

Soit: $\overrightarrow{I J}=\frac{2}{3} \overrightarrow{E F}+\overrightarrow{F G}+\frac{2}{3} \overrightarrow{G C} \quad$ (d'après (3) et (4)). Soit : $\overrightarrow{I J}=\frac{2}{3}(\overrightarrow{E F}+\overrightarrow{G C})+\overrightarrow{F G} \quad$ c.q.f.d. 2.b. Par conséquent : $\overrightarrow{I J}=\frac{2}{3}(\overrightarrow{E F}+\overrightarrow{F B})+\overrightarrow{F G} \quad$ (d'après (1)).

Soit : $\overrightarrow{I J}=\frac{2}{3} \overrightarrow{E B}+\overrightarrow{F G}$ (Chasles) c.q.f.d. 2.c. Par conséquent : $\overrightarrow{I J}=\frac{2}{3}(\overrightarrow{E C}-\overrightarrow{B C})+\overrightarrow{F G} \quad$ (Chasles).

Soit: $\overrightarrow{I J}=\frac{2}{3}(\overrightarrow{E C}-\overrightarrow{F G})+\overrightarrow{F G} \quad$ (d'après (2)). Soit: $\overrightarrow{I J}=\frac{2}{3} \overrightarrow{E C}-\frac{2}{3} \overrightarrow{F G}+\overrightarrow{F G}$. Soit : $\overrightarrow{I J}=\frac{2}{3} \overrightarrow{E C}+\frac{1}{3} \overrightarrow{F G} \quad$ c.q.f.d. 2.d. Donc il existe des nombres réels $x$ et $y$ tels que $\overrightarrow{I J}=x \overrightarrow{E C}+y \overrightarrow{F G}$.

Et par là, les vecteurs $\overrightarrow{F G}, \overrightarrow{I J}$ et $\overrightarrow{E C}$ sont coplanaires.

3. Méthode 2.

Préambule. ABCDEFGH est un cube, et par là : $\quad \overrightarrow{E F}=-\overrightarrow{G H} \quad$ (1). Et comme $: \overrightarrow{E I}=\frac{1}{3} \overrightarrow{E F}$, on a : $\quad \overrightarrow{I F}=-\frac{2}{3} \overrightarrow{G H}$ Enfin, on a: $\quad \overrightarrow{G J}=\frac{2}{3} \overrightarrow{G C}$ (3). 3.a. On a : $\overrightarrow{E C}=\overrightarrow{E F}+\overrightarrow{F G}+\overrightarrow{G C} \quad$ (Chasles).

Soit : $\overrightarrow{E C}=-\overrightarrow{G H}-\overrightarrow{G F}+\overrightarrow{G C} \quad$ (d'après (1)). 3.b. On a : $\overrightarrow{I J}=\overrightarrow{I F}+\overrightarrow{F G}+\overrightarrow{G J} \quad$ (Chasles).

Soit: $\overrightarrow{I J}=-\frac{2}{3} \overrightarrow{G H}-\overrightarrow{G F}+\frac{2}{3} \overrightarrow{G C} \quad$ (d'après (2) et (3)).

3．c．On pose：（E）$\quad a \cdot \overrightarrow{E C}+b \cdot \overrightarrow{I J}=\overrightarrow{F G}$ ． On a ：（E）$\Leftrightarrow a \cdot(-\overrightarrow{G H}-\overrightarrow{G F}+\overrightarrow{G C})+b \cdot\left(-\frac{2}{3} \overrightarrow{G H}-\overrightarrow{G F}+\frac{2}{3} \overrightarrow{G C}\right)=\overrightarrow{F G} \quad$（d＇après 3．a．et 3．b．）． Soit ：（E）$\Leftrightarrow\left(-a-\frac{2}{3} b\right) \overrightarrow{G H}+(-a-b) \overrightarrow{G F}+\left(a+\frac{2}{3} b\right) \overrightarrow{G C}=-\overrightarrow{G F}$ ． Par unicité de la décomposition d＇un vecteur dans une base（ici la base（ $\overrightarrow{G C}, \overrightarrow{G H}$ ， $\overrightarrow{G F})$ ），on en déduit que ： （E）$\Leftrightarrow\left{\begin{array}{l}-a-\frac{2}{3} b=0 \ -a-b=-1 \ a+\frac{2}{3} b=0\end{array} \Leftrightarrow\left{\begin{array}{c}a=-\frac{2}{3} b \ \frac{2}{3} b-b=-1 \ a=-\frac{2}{3} b\end{array} \Leftrightarrow\left{\begin{array}{c}a=-\frac{2}{3} b \ b=3\end{array} \Leftrightarrow\left{\begin{array}{c}a=-2 \ b=3\end{array}\right.\right.\right.\right.$ Le système admet un couple solution $(a, b)=(-2 ; 3)$ ．

3．d．Donc il existe des nombres réels $a$ et $b$ tels que $a \cdot \overrightarrow{E C}+b \cdot \overrightarrow{I J}=\overrightarrow{F G}$ ． Et par là，les vecteurs $\overrightarrow{F G}, \overrightarrow{I J}$ et $\overrightarrow{E C}$ sont coplanaires．

4．Méthode 3.

4．a．Dans le repère（ $G, \overrightarrow{G C}, \overrightarrow{G H}, \overrightarrow{G F}$ ），on a： $F(0 ; 0 ; 1), G(0 ; 0 ; 0), I\left(0 ; \frac{2}{3} ; 1\right), J\left(\frac{2}{3} ; 0 ; 0\right), E(0 ; 1 ; 1)$ et $C(1 ; 0 ; 0)$ ．

3．b．On obtient alors： $\overrightarrow{E C}(1 ;-1 ;-1)$ ， $\overrightarrow{I J}\left(\frac{2}{3} ;-\frac{2}{3} ;-1\right)$, et $\overrightarrow{F G}(0 ; 0 ;-1)$ ．

3．c．On pose：（E）$\quad a \cdot \overrightarrow{E C}+b \cdot \overrightarrow{I J}=\overrightarrow{F G}$ ． $(\mathrm{E}) \Leftrightarrow\left{\begin{array}{c}a+\frac{2}{3} b=0 \ -a-\frac{2}{3} b=0 \ -a-b=-1\end{array} \Leftrightarrow\left{\begin{array}{c}a=-\frac{2}{3} b \ a=-\frac{2}{3} b \ \frac{2}{3} b-b=-1\end{array} \Leftrightarrow\left{\begin{array}{c}a=-\frac{2}{3} b \ b=3\end{array} \Leftrightarrow\left{\begin{array}{c}a=-2 \ b=3\end{array}\right.\right.\right.\right.$ Le système admet un couple solution $(a, b)=(-2 ; 3)$ ． 3.d. Donc il existe des nombres réels $a$ et $b$ tels que $a \cdot \overrightarrow{E C}+b \cdot \overrightarrow{I J}=\overrightarrow{F G}$. Et par là, les vecteurs $\overrightarrow{F G}, \overrightarrow{I J}$ et $\overrightarrow{E C}$ sont coplanaires.

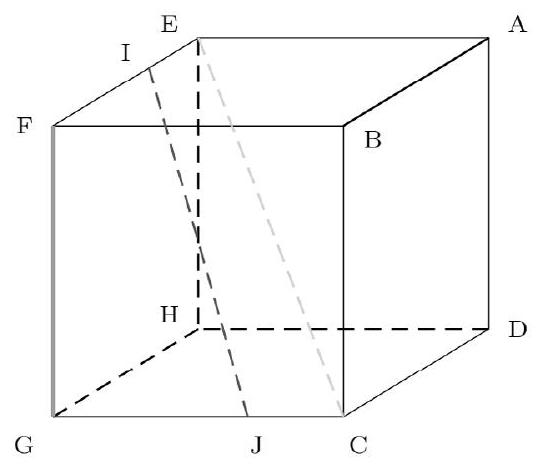
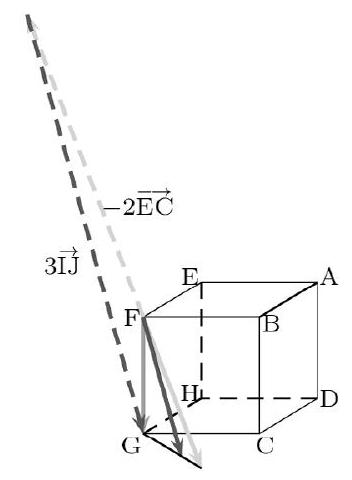
Le fait que ces 3 vecteurs appartiennent au même plan vectoriel n'est pas graphiquement évident. Pour une meilleure visualisation du problème, j'ai tracé des représentants de ces vecteurs issus du même point F. La propriété de coplanarité saute alors aux yeux avertis...

Et, pour finir, $j$ 'ai fait apparaître ci-dessous le fait que $-2 \overrightarrow{E C}+3 \overrightarrow{I J}=\overrightarrow{F G}$.

Exercice 4

ABCDEFGH est un cube de côté non nul. Les points I et J vérifient : $\overrightarrow{E I}=\frac{1}{3} \overrightarrow{E F}$ et $\overrightarrow{D J}=\frac{1}{3} \overrightarrow{D H}$. On veut montrer que la droite (EJ) est parallèle au plan (GDI). Nous allons procéder selon deux méthodes différentes.

Première méthode

a. Déterminer graphiquement deux nombres réels $x$ et $y$ tels que $\overrightarrow{E J}=x \overrightarrow{G D}+y \overrightarrow{G I}$ (ne pas justifier). Il est vivement conseillé de connaître la relation de Chasles pour espérer répondre aux questions qui suivent... b. Comme ABCDEFGH est un cube de côté non nul, $(\overrightarrow{H G}, \overrightarrow{H D}, \overrightarrow{H E})$ constitue une base de l'espace. Décomposer chacun des vecteurs $\overrightarrow{E J}, \overrightarrow{G D}$ et $\overrightarrow{G I}$ dans la base ( $\overrightarrow{H G}, \overrightarrow{H D}, \overrightarrow{H E}$ ). c. Prouver votre conjecture graphique. d. Conclure.

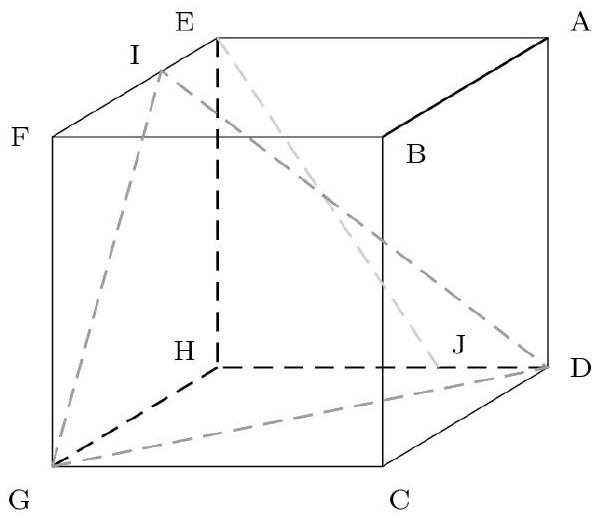
Seconde méthode

a. Comme ABCDEFGH est un cube de côté non nul, ( $G, \overrightarrow{G C}, \overrightarrow{G H}, \overrightarrow{G F}$ ) constitue un repère de l'espace. Déterminer graphiquement les coordonnées de $\overrightarrow{E J}, \overrightarrow{G D}$ et $\overrightarrow{G I}$ (ne pas justifier). b. Déterminer par le calcul deux nombres réels $x$ et $y$ tels que $\overrightarrow{E J}=x \overrightarrow{G D}+y \overrightarrow{G I}$. c. Conclure.

Corrigé

Première méthode

Dans cet exercice, l'astuce est de décomposer les vecteurs à l'aide de la relation de Chasles.

Il est alors conseillé de «suivre» les traits de construction, ce qui permettra une utilisation efficace des hypothèses données dans l'énoncé. a. On traçe le représentant du vecteur $\overrightarrow{E J}$ issu de I (voir la figure qui suit).

Il semble que: $\overrightarrow{E J}=-\overrightarrow{G I}+\frac{2}{3} \overrightarrow{G D}$. On aurait donc : $y=-1$ et $x=\frac{2}{3}$. b. Préambule.

ABCDEFGH est un cube, et par là : $\quad \overrightarrow{G F}=\overrightarrow{H E}$ et comme $\overrightarrow{E I}=\frac{1}{3} \overrightarrow{E F}$, on a de plus : $\quad \overrightarrow{F I}=-\frac{2}{3} \overrightarrow{H G}$ Enfin, comme $: \overrightarrow{D J}=\frac{1}{3} \overrightarrow{D H}$, on a : $\quad \overrightarrow{H J}=\frac{2}{3} \overrightarrow{H D}$

On a $: \overrightarrow{E J}=\overrightarrow{E H}+\overrightarrow{H J} \quad$ (Chasles). Soit: $\overrightarrow{E J}=-\overrightarrow{H E}+\frac{2}{3} \overrightarrow{H D} \quad$ (d'après (3)).

On a : $\overrightarrow{G D}=\overrightarrow{G H}+\overrightarrow{H D} \quad$ (Chasles). Soit : $\overrightarrow{G D}=-\overrightarrow{H G}+\overrightarrow{H D}$. On a : $\overrightarrow{G I}=\overrightarrow{G F}+\overrightarrow{F I} \quad$ (Chasles). Soit : $\overrightarrow{G I}=\overrightarrow{H E}-\frac{2}{3} \overrightarrow{H G} \quad$ (d'après (1) et (2)). c. Prouvons la conjecture du a. grace aux décompositions du b.

Pour prouver une égalité, il suffit de partir d'un membre, et d'arriver à l'autre... On calcule : $-\overrightarrow{G I}+\frac{2}{3} \overrightarrow{G D}=-\left(\overrightarrow{H E}-\frac{2}{3} \overrightarrow{H G}\right)+\frac{2}{3}(-\overrightarrow{H G}+\overrightarrow{H D})$. D'où : $-\overrightarrow{G I}+\frac{2}{3} \overrightarrow{G D}=-\overrightarrow{H E}+\frac{2}{3} \overrightarrow{H G}-\frac{2}{3} \overrightarrow{H G}+\frac{2}{3} \overrightarrow{H D}$. D'où : $-\overrightarrow{G I}+\frac{2}{3} \overrightarrow{G D}=-\overrightarrow{H E}+\frac{2}{3} \overrightarrow{H D}$. Soit : $-\overrightarrow{G I}+\frac{2}{3} \overrightarrow{G D}=\overrightarrow{E J} \quad$ c.q.f.d. d. Il est clair que les vecteurs $\overrightarrow{G I}$ et $\overrightarrow{G D}$ sont directeurs du plan (GDI).

Et comme on a montré qu'il existe deux nombres réels $x$ et $y$ tels que $\overrightarrow{E J}=x \overrightarrow{G D}+y \overrightarrow{G I}$, on en déduit que le vecteur $\overrightarrow{E J}$ appartient à la direction vectorielle du plan (GDI). Et comme ce vecteur $\overrightarrow{E J}$ est un vecteur directeur de la droite (EJ), cette dernière est donc parallèle au plan (GDI). c.q.f.d.

Seconde méthode

a. On obtient : $\overrightarrow{E J}\left(\frac{2}{3}, 0,-1\right), \overrightarrow{G D}(1,1,0)$ et $\overrightarrow{G I}\left(0, \frac{2}{3}, 1\right)$. b. $\overrightarrow{E J}=x \overrightarrow{G D}+y \overrightarrow{G I} \Leftrightarrow\left{\begin{array}{l}\frac{2}{3}=1 x+0 y \ 0=1 x+\frac{2}{3} y \ -1=0 x+1 y\end{array} \Leftrightarrow\left{\begin{array}{c}\frac{2}{3}=x \ 0=x+\frac{2}{3} y \ -1=y\end{array}\right.\right.$

Il est clair que la seconde égalité est bien vérifiée, et par là : $\overrightarrow{E J}=x \overrightarrow{G D}+y \overrightarrow{G I} \Leftrightarrow\left{\begin{array}{c}x=\frac{2}{3} \ y=-1\end{array}\right.$ c. La conclusion est la même qu'au d. de la première méthode...

Exercice 5

Nous allons démontrer ici quelques résultats que vous avez peut-être déjà vus par ailleurs. Ils concernent le centre de gravité d'un triangle et celui d'une pyramide.

ABCD est tétraèdre non aplati. $(\overrightarrow{A B}, \overrightarrow{A C}, \overrightarrow{A D})$ constitue donc une base de l'espace. Et $(\overrightarrow{A B}, \overrightarrow{A C})$ constitue donc une base du plan vectoriel associé à (ABC). Une figure est tracée page suivante.

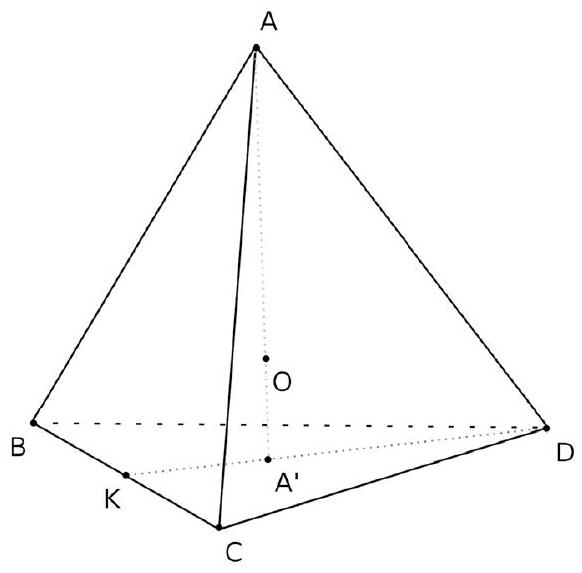
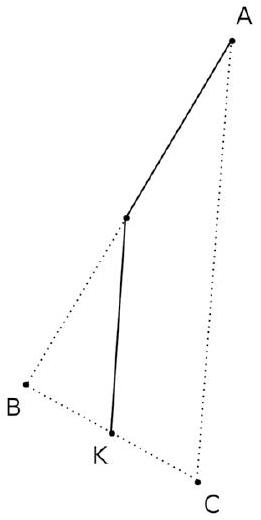
1. Soit K le milieu de l'arête $[\mathrm{BC}]$.

Décomposer graphiquement le vecteur $\overrightarrow{A K}$ dans la base $(\overrightarrow{A B}, \overrightarrow{A C})$. 2. Prouver votre conjecture à l'aide de la relation de Chasles. 3. Soit A'le centre de gravité de BCD.

On a donc $: \overrightarrow{K A^{\prime}}=\frac{1}{3} \overrightarrow{K D}$. Décomposer graphiquement le vecteur $\overrightarrow{A A^{\prime}}$ dans la base $(\overrightarrow{A B}, \overrightarrow{A C}, \overrightarrow{A D})$. 4. Prouver votre conjecture à l'aide de la relation de Chasles.

Il est conseillé de montrer que : $\overrightarrow{A A^{\prime}}=\frac{1}{3} \overrightarrow{K D}-\overrightarrow{K A}$, puis de décomposer $\overrightarrow{K D}$ et $\overrightarrow{K A}$ dans la base $(\overrightarrow{A B}, \overrightarrow{A C}, \overrightarrow{A D})$. 5. En déduire que : $\overrightarrow{A^{\prime} B}+\overrightarrow{A^{\prime} C}+\overrightarrow{A^{\prime} D}=\overrightarrow{0}$ (utiliser à nouveau la relation de Chasles). 6. Soit O le centre de gravité du tétraèdre.

Le point O est défini par l'égalité : $\overrightarrow{A O}=\frac{1}{4}(\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A D})$. En utilisant la relation de Chasles et l'égalité obtenue au 5 , montrer que : $\overrightarrow{A^{\prime} O}=\frac{1}{4} \overrightarrow{A^{\prime} A}$.

Corrigé

1. Graphiquement, on obtient : $\overrightarrow{A K}=\frac{1}{2} \overrightarrow{A B}+\frac{1}{2} \overrightarrow{A C}$.
2. Prouvons cette conjecture.

On a: $\frac{1}{2} \overrightarrow{A B}+\frac{1}{2} \overrightarrow{A C}=\frac{1}{2}(\overrightarrow{A K}+\overrightarrow{K B}+\overrightarrow{A K}+\overrightarrow{K C}) \quad$ (Chasles). Soit : $\frac{1}{2} \overrightarrow{A B}+\frac{1}{2} \overrightarrow{A C}=\frac{1}{2}(2 \overrightarrow{A K}+\overrightarrow{K B}+\overrightarrow{K C})$. Or, comme K est le milieu de $[\mathrm{BC}]$, on a : $\overrightarrow{K B}+\overrightarrow{K C}=\overrightarrow{0}$. Donc on obtient : $\frac{1}{2} \overrightarrow{A B}+\frac{1}{2} \overrightarrow{A C}=\overrightarrow{A K} \quad$ c.q.f.d. 3. Graphiquement, on obtient : $\overrightarrow{A A^{\prime}}=\frac{1}{3} \overrightarrow{A B}+\frac{1}{3} \overrightarrow{A C}+\frac{1}{3} \overrightarrow{A D}$. 4. Prouvons cette conjecture.

Comme on a $: \overrightarrow{K A^{\prime}}=\frac{1}{3} \overrightarrow{K D}$, on a : $\overrightarrow{K A}+\overrightarrow{A A^{\prime}}=\frac{1}{3} \overrightarrow{K D} \quad$ (Chasles). Soit : $\overrightarrow{A A^{\prime}}=\frac{1}{3} \overrightarrow{K D}-\overrightarrow{K A} \quad$ (1).

Par ailleurs, on a vu que : $\overrightarrow{A K}=\frac{1}{2} \overrightarrow{A B}+\frac{1}{2} \overrightarrow{A C}$ De même, on obtient : $\overrightarrow{D K}=\frac{1}{2} \overrightarrow{D B}+\frac{1}{2} \overrightarrow{D C}$. On utilise à nouveau Chasles pour décomposer $\overrightarrow{D B}$ et $\overrightarrow{D C}$. On obtient alors : $\overrightarrow{D K}=\frac{1}{2}(\overrightarrow{D A}+\overrightarrow{A B})+\frac{1}{2}(\overrightarrow{D A}+\overrightarrow{A C})$

Et donc, d'après (2) et (3), l'égalité (1) devient : $\overrightarrow{A A^{\prime}}=-\frac{1}{3}\left(\frac{1}{2}(\overrightarrow{D A}+\overrightarrow{A B})+\frac{1}{2}(\overrightarrow{D A}+\overrightarrow{A C})\right)+\frac{1}{2} \overrightarrow{A B}+\frac{1}{2} \overrightarrow{A C}$. Soit : $\overrightarrow{A A^{\prime}}=-\frac{1}{6}(\overrightarrow{D A}+\overrightarrow{A B})-\frac{1}{6}(\overrightarrow{D A}+\overrightarrow{A C})+\frac{1}{2} \overrightarrow{A B}+\frac{1}{2} \overrightarrow{A C}$. Soit : $\overrightarrow{A A^{\prime}}=\left(-\frac{1}{6}+\frac{1}{2}\right) \overrightarrow{A B}+\left(-\frac{1}{6}+\frac{1}{2}\right) \overrightarrow{A C}+\left(-\frac{1}{6}-\frac{1}{6}\right) \overrightarrow{D A}$. Soit : $\overrightarrow{A A^{\prime}}=\frac{1}{3} \overrightarrow{A B}+\frac{1}{3} \overrightarrow{A C}+\frac{1}{3} \overrightarrow{A D} \quad$ c.q.f.d. 5. Montrons que $\overrightarrow{A^{\prime} B}+\overrightarrow{A^{\prime} C}+\overrightarrow{A^{\prime} D}=\overrightarrow{0}$.

On a : $\overrightarrow{A^{\prime} B}+\overrightarrow{A^{\prime} C}+\overrightarrow{A^{\prime} D}=\overrightarrow{A^{\prime} A}+\overrightarrow{A B}+\overrightarrow{A^{\prime} A}+\overrightarrow{A C}+\overrightarrow{A^{\prime} A}+\overrightarrow{A D} \quad$ (Chasles) . Soit : $\overrightarrow{A^{\prime} B}+\overrightarrow{A^{\prime} C}+\overrightarrow{A^{\prime} D}=3 \overrightarrow{A^{\prime} A}+\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A D}$. Or, comme $\overrightarrow{A A^{\prime}}=\frac{1}{3}(\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A D})$, on a : $3 \overrightarrow{A A^{\prime}}=\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A D}$. Donc on obtient : $\overrightarrow{A^{\prime} B}+\overrightarrow{A^{\prime} C}+\overrightarrow{A^{\prime} D}=3 \overrightarrow{A^{\prime} A}+3 \overrightarrow{A A^{\prime}}$. Et donc : $\overrightarrow{A^{\prime} B}+\overrightarrow{A^{\prime} C}+\overrightarrow{A^{\prime} D}=\overrightarrow{0} \quad$ c.q.f.d. 6. On a : $\overrightarrow{A O}=\frac{1}{4}(\overrightarrow{A B}+\overrightarrow{A C}+\overrightarrow{A D})$.

Donc : $\overrightarrow{A A^{\prime}}+\overrightarrow{A^{\prime} O}=\frac{1}{4}\left(\overrightarrow{A A^{\prime}}+\overrightarrow{A^{\prime} B}+\overrightarrow{A A^{\prime}}+\overrightarrow{A^{\prime} C}+\overrightarrow{A A^{\prime}}+\overrightarrow{A^{\prime} D}\right) \quad$ (Chasles) $\overrightarrow{A^{\prime} O}=-\overrightarrow{A A^{\prime}}+\frac{1}{4}\left(3 \overrightarrow{A A^{\prime}}+\overrightarrow{A^{\prime} B}+\overrightarrow{A^{\prime} C}+\overrightarrow{A^{\prime} D}\right)$. Or on a vu que : $\overrightarrow{A^{\prime} B}+\overrightarrow{A^{\prime} C}+\overrightarrow{A^{\prime} D}=\overrightarrow{0} \quad$ (question 5.). Donc on obtient : $\overrightarrow{A^{\prime} O}=-\overrightarrow{A A^{\prime}}+\frac{3}{4} \overrightarrow{A A^{\prime}}$. Soit : $\overrightarrow{A^{\prime} O}=\frac{1}{4} \overrightarrow{A^{\prime} A} \quad$

c.q.f.d.