Exercices : Combinatoire et dénombrement

Exercices corrigés

Exercice 1

Le professeur de maths dispose de 6 exercices de dénombrement, 15 exercices d'analyse et 9 exercices de géométrie.

• Il compose un devoir de fin d'année contenant un exercice de dénombrement, un exercice d'analyse et un exercice de géométrie. L'ordre des exercices n'a pas d'importance. Combien de devoirs différents peut-il composer ?
• Le professeur se rend compte que de tels devoir sont trop long. Il pense qu'un devoir contenant exactement 2 exercices de types différents suffit. L'ordre des exercices n'a toujours pas d'importance. Combien de devoirs différents peut-il finalement composer?

Corrigé

• On utilise le principe multiplicatif. On calcule : $6 \times 15 \times 9=810$.

Le professeur peut composer $\mathbf{8 1 0}$ devoirs différents.

• On cherche combien y a-t-il de devoirs contenant un exercice de dénombrement et un exercice d'analyse. On calcule : $6 \times 15=90$.

Le professeur peut composer 90 devoirs de ce type. On fait de même avec les devoirs contenant un exercice de dénombrement et un exercice de géométrie. On calcule : $6 \times 9=54$. Le professeur peut composer 54 devoirs de ce type. On recommence avec les devoirs contenant un exercice d'analyse et un exercice de géométrie. On calcule : $15 \times 9=135$. Le professeur peut composer 135 devoirs de ce type. On utilise le principe additif. On calcule : $90+54+135=279$. Le professeur peut composer 279 devoirs différents.

Exercice 2

Soit E un ensemble à $n$ éléments (avec $n$ entier non nul).

• Combien y a-t-il de couples ( $\mathrm{A}, \mathrm{B}$ ) de parties de E tels que $A \cup B=E$ et $A \cap B=\varnothing$ ?
• On suppose que A est une partie à $p$ éléments de E .

Combien y a-t-il de parties B de E tels que $A \cup B=E$ ?

Corrigé

• Un couple (A,B) est convenable si et seulement si B est le complémentaire de A dans E. Donc un couple est convenable si et seulement si il est du type $(A, \bar{A})$.

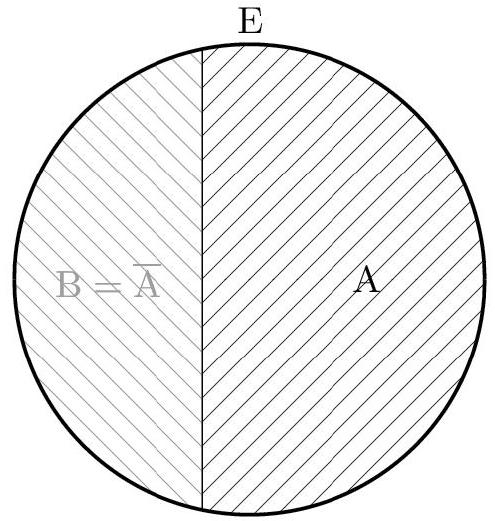
Il y a donc autant de couples $(A, \bar{A})$ que de parties A de E . Et, comme E est un ensemble à $n$ éléments, il y en a $\square$ $2^{n}$ .

• Une partie B est convenable si et seulement si $B=\bar{A} \cup C$, où C est une partie de A.

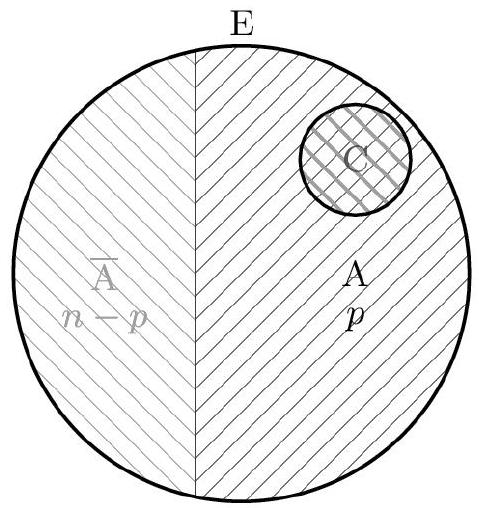
Il y a donc autant de parties B convenables que de parties C de A . Et , comme A est un ensemble à $p$ éléments, il y en a $2^{p}$.

Exercice 3

• Simplifier l'écriture de $\frac{99!}{96!}-941093$
• Dénombrer les anagrammes du mot MATHS.
• Combien y a-t-il de nombres de 10 chiffres tous différents alternant chiffres pairs et impairs ? Notons que les nombres 1234567890 et 2345678901 sont convenables, mais pas le nombre 0123456789 qui n'a en fait que 9 chiffres (il s'écrit 123456789).

Corrigé

• $\frac{99!}{96!}-941093=\frac{99 \times 98 \times 97 \times 96!}{96!}-941093=99 \times 98 \times 97-941093=1$
• Un anagramme correspond à une permutation des lettres d'un mot. Comme MATHS a 5 lettres toutes différentes, on calcule donc : $5!=120$. Le mot MATHS possède donc 120 anagrammes.
• Il y a 4 possibilités paires et 5 possibilités impaires pour le premier chiffre (qui ne peut être nul). Supposons que le premier chiffre soit pair. Cela donne 4 possibilités (car il ne peut être nul). On répartit alors les 4 autres chiffres pairs sur leurs emplacements (de rangs 3, 5, 7 et 9 ). Cela donne $4!$ permutations possibles. On répartit les 5 chiffres impairs sur leurs emplacements (de rangs $2,4,6,8$ et 10 ). Cela donne 5! permutations possibles. On calcule alors : $4 \times 4!\times 5!=11520$.

Il y a $\mathbf{1 1 5 2 0}$ nombres convenables dont le premier chiffre est pair. Comptons de même les nombres convenables dont le premier chiffre est impair. Supposons donc que le premier chiffre soit impair. Cela donne 5 possibilités. On répartit alors les 4 autres chiffres impairs sur leurs emplacements (de rangs 3, 5, 7 et 9 ). Cela donne 4 ! permutations possibles. On répartit les 5 chiffres pairs sur leurs emplacements (de rangs 2, 4, 6, 8 et 10). Cela donne 5 ! permutations possibles. On calcule alors : $5 \times 4!\times 5!=5!\times 5!=14400$. Il y a $\mathbf{1 4 4 0 0}$ nombres convenables dont le premier chiffre est impair. On utilise alors le principe additif. On somme : $11520+14400=25920$. Il y a donc 25920 nombres de 10 chiffres tous différents alternant chiffres pairs et impairs.

Exercice 4

• Dénombrer le nombre de tiercés possibles avec 15 chevaux au départ de la course.
• On tire 3 boules successivement et sans remise d'une urne contenant 7 boules numérotées de 1 à 7 . Combien y a-t-il de tirages possibles ? Combien y a-t-il de tirages dont le produit des numéros vaut 30 ?
• Dénombrer les anagrammes du mot MAMIE.
• Dénombrer les anagrammes du mot MICHEL commençant et finissant par une consonne.

Corrigé

• Un tiercé est ici un arrangement sans répétition de 3 éléments parmi 15 (les numéros des 3 premiers). On calcule donc : $A_{15}^{3}=\frac{15!}{12!}=15 \times 14 \times 13=2730$. Il y a 2730 tiercés possibles.
• Un tirage est un arrangement sans répétition de 3 éléments parmi 7 (les numéros des 3 boules). On calcule donc : $A_{7}^{3}=\frac{7!}{4!}=7 \times 6 \times 5=210$. Il y a 210 tirages possibles. Dénombrons maintenant les tirages dont le produit des numéros vaut 30 . On a : $30=1 \times 2 \times 3 \times 5$. On veut un produit de 3 nombres entre 1 et 7 .

Les seules possibilités sont : $30=1 \times 6 \times 5$ et $30=2 \times 3 \times 5$. Donc un tirage favorable correspond à une permutation des numéros 1,6 et 5 ou 2 , 3 et 5 . On calcule donc : $3!+3!=12$. Il y a 12 tirages dont le produit des numéros vaut 30 .

• MAMIE a 5 lettres dont 2 identiques.

Le rang des lettres A , I et E correspond à un arrangement sans répétition de 3 éléments parmi 5 (par exemple, pour MAMIE, cet arrangement est ( $2,4,5$ )). Une fois ces 3 lettres placées, les deux M vont dans les places restantes. On dénombre donc le nombre d'arrangements sans répétition de 3 éléments parmi 5.

On calcule donc : $\mathrm{A}_{5}^{3}=\frac{5!}{2!}=5 \times 4 \times 3=60$. Le mot MAMIE possède donc 60 anagrammes.

• Le placement des deux consonnes de début et de fin (choisies parmi les quatre possibles) est un arrangement sans répétition de 2 éléments parmi 4. On calcule donc : $A_{4}^{2}=\frac{4!}{2!}=4 \times 3=12$. Il y a donc 12 choix possibles pour les consonnes extérieures. Une fois ces 2 lettres placées, les 4 autres lettres vont dans les places restantes. On dénombre alors le nombre de permutations de 4 éléments. On calcule donc : $4!=24$. Et finalement, on calcule : $12 \times 24=288$. Le mot MICHEL possède donc 288 anagrammes commençant et finissant par une consonne.

Exercice 5

• Combien y a-t-il de nombres de quatre chiffres, le premier étant non nul ?
• Combien y a-t-il de nombres de quatre chiffres distincts tous strictement supérieurs à 1 ?
• Combien y a-t-il de nombres de quatre chiffres distincts, le premier étant non nul ?
• Combien y a-t-il de nombres de quatre chiffres avec au moins 2 chiffres semblables, le premier étant non nul?

Corrigé

• Le premier chiffre est strictement supérieur à 0 , les 3 autres sont quelconques.

On calcule donc : $9 \times 10 \times 10 \times 10=9000$.

Il y a 9000 nombres à quatre chiffres, le premier étant non nul. On aura noté que ce sont les nombres de 1000 à 9999 (et que $9999-1000+1=9000$ )

• Les 4 chiffres (distincts) correspondent à un arrangement sans répétition de 4 éléments parmi 8 (les chiffres de 2 à 9 ). On calcule donc : $A_{8}^{4}=\frac{8!}{4!}=8 \times 7 \times 6 \times 5=1680$. Il y a 1680 nombres de quatre chiffres distincts tous strictement supérieurs à 1 .
• Il y a 9 possibilités pour le premier chiffre (non nul).

Les 3 autres chiffres (distincts entre eux et du premier) correspondent à un arrangement sans répétition de 3 éléments parmi 9 . On calcule donc : $A_{9}^{3}=\frac{9!}{6!}=9 \times 8 \times 7=504$. On calcule ensuite : $9 \times 504=4536$. Il y a 4536 nombres de quatre chiffres distincts, le premier étant non nul.

• Si un nombre a 4 chiffres, le premier étant non nul, alors : soit les 4 chiffres sont distincts, soit il a au moins 2 chiffres semblables. On calcule donc : $9000-4536=4464$ (voir ci-dessus). Il y a 4464 nombres de quatre chiffres avec au moins 2 chiffres semblables, le premier étant non nul.

Exercice 6

• Un club d'échecs organise un tournoi interne entre ses 10 membres. Chaque joueur doit rencontrer tous les autres une seule fois. Combien doit-on organiser de parties ?
• Un club sportif doit envoyer une délégation pour une rencontre à l'étranger. Cette délégation doit être composée de 3 femmes et 2 hommes. Le club possède 20 membres, 12 femmes et 8 hommes. Combien de délégations différentes sont-elles possibles ?
• Combien y a-t-il de mains de 5 cartes dans un jeu de 32 cartes ?
• Combien y a-t-il de mains de 5 cartes comportant exactement 2 trèfles dans un jeu de 32 cartes ?
• Combien y a-t-il de mains de 5 cartes comportant le valet de pique et au moins 2 cœurs dans un jeu de 32 cartes ?

Corrigé

• Une partie correspond à une combinaison de 2 éléments parmi 10 (les noms des deux joueurs, l'ordre n'ayant pas d'importance). On calcule donc : $\binom{10}{2}=\frac{10!}{8!\times 2!}=\frac{10 \times 9}{2 \times 1}=45$. Le club doit organiser 45 parties.
• Le choix des femmes correspond à une combinaison de 3 éléments parmi 12 (les noms des trois femmes, l'ordre n'ayant pas d'importance). On calcule donc : $\binom{12}{3}=\frac{12!}{9!\times 3!}=\frac{12 \times 11 \times 10}{3 \times 2 \times 1}=220$. Le choix des hommes correspond à une combinaison de 2 éléments parmi 8 (les noms des deux hommes, l'ordre n'ayant pas d'importance). On calcule donc : $\binom{8}{2}=\frac{8!}{6!\times 2!}=\frac{8 \times 7}{2 \times 1}=28$. On utilise alors le principe multiplicatif. On calcule : $220 \times 28=6160$. Il y a 6160 délégations possibles.
• Une main de 5 cartes correspond à une combinaison de 5 éléments parmi 32 (l'ordre n'ayant pas d'importance). On calcule donc : $\binom{32}{5}=\frac{32!}{27!\times 53!}=\frac{32 \times 31 \times 30 \times 29 \times 28}{5 \times 4 \times 3 \times 2 \times 1}=201376$. Il y a 201376 mains de 5 cartes dans un jeu de 32 cartes.
• Les 2 trèfles (choisis parmi les 8 ) correspondent à une combinaison de 2 éléments parmi 8. Les 3 autres cartes (choisis parmi les 24) correspondent à une combinaison de 3 éléments parmi 24. On utilise alors le principe multiplicatif. On calcule : $\binom{8}{2} \times\binom{ 24}{3}=28 \times 2024=56672$. Il y a 56672 mains de 5 cartes comportant exactement 2 trèfles dans un jeu de 32 cartes.
• On choisit déjà le valet de pique.

Puis on choisit au moins 2 cœurs, c'est-à-dire soit 2, soit 3, soit 4 cœurs parmi les 8 Cœurs.

Et on complète avec des cartes qui ne sont ni des cœurs, ni le valet de pique choisies parmi les 23 cartes possibles. On calcule donc la somme $s$ : $s=1 \times\left(\binom{8}{2} \times\binom{ 23}{2}+\binom{8}{3} \times\binom{ 23}{1}+\binom{8}{4} \times\binom{ 23}{0}\right)$. Soit : $s=28 \times 253+56 \times 23+70 \times 1=8442$. Il y a 8442 mains de 5 cartes comportant le valet de pique et au moins 2 cœurs dans un jeu de 32 cartes.

Exercice 7

Un joueur va recevoit une main de 5 cartes d'un jeu de 52.

1. Quelle est la probabilité que cette main contienne au moins un as ?
2. Quelle est la probabilité que cette main contienne un carré (c'est-à-dire quatre cartes de même valeur) ?
3. Quelle est la probabilité que cette main contienne un full (c'est-à-dire un brelan (trois cartes de même valeur) et une paire (deux autres cartes de même valeur), par exemple 3 as et 2 rois) ?
4. Quelle est la probabilité que cette main contienne un brelan (trois cartes de même valeur), mais pas de carré ni de full ?

Corrigé

$\operatorname{Card} \Omega=\binom{52}{5}=2598$ 960. Il y a équiprobabilité.

1. Soit E : «la main ne contient pas d'as». On cherche $p(\bar{E})$.

Card $\mathrm{E}=\binom{48}{5}=1712304$. Donc : $p(E)=\frac{1712304}{2598960}$. Et par là : $p(\bar{E})=1-\frac{1712304}{2598960}=\frac{886656}{2598960} \approx 0,34$. La probabilité que la main contienne au moins un as vaut environ 0,34 . 2. Soit C : «la main contient un carré». On cherche $p(C)$.

Il y a 13 choix possibles pour la valeur des cartes constituant le carré (parmi As, Roi, Dame, Valet, 10, 9, 8, 7, 6, 5, 4, 3, 2). Cette valeur étant choisie, il ne reste plus qu'une carte à ajouter pour obtenir une main complète. Cette carte est à choisir parmi les 48 autres cartes possibles. Donc : Card C $=13 \times 48=624$. Et par là : $p(C)=\frac{624}{2598960} \approx 0,00024$.

La probabilité que la main contienne un carré vaut environ 0,0024 . 3. Soit F : «la main contient un full». On cherche $p(F)$.

On choisit d'abord la valeur des 3 cartes du brelan. Il y a 13 choix. On choisit alors ces 3 cartes de même valeur parmi les 4 possibles. Il y a $\binom{4}{3}=4$ choix possibles. On choisit ensuite la valeur des 2 cartes de la paire. Il reste 12 possibilités. Puis on choisit ces 2 cartes de même valeur. Il y a $\binom{4}{2}=6$ possibilités. Et par là : Card $\mathrm{F}=13 \times 4 \times 12 \times 6=3744$. Et par là : $p(F)=\frac{3744}{2598960} \approx 0,0014$. La probabilité que la main contienne un full vaut environ 0,0014 . 4. Soit B : « la main contient un brelan, mais pas de carré ni de full». On cherche $p(B)$. On choisit d'abord la valeur des 3 cartes du brelan. Il y a 13 choix. On choisit alors ces 3 cartes de même valeur parmi les 4 possibles. Il y a $\binom{4}{3}=4$ choix possibles. On choisit ensuite les 2 autres cartes parmi les 48 possibilités restantes (et non pas 49 , sinon, on risquerait d'obtenir un carré). Il y a $\binom{48}{2}=1128$ possibilités. On calcule alors : $13 \times 4 \times 1128=58656$. Et comme on ne veut pas de full, on obtient : Card B $=58656-3744=54912$. Et donc : $p(B)=\frac{54912}{2598960} \approx 0,021$. La probabilité que la main contienne un un brelan, mais pas de carré ni de full vaut environ 0,021 .

Exercice 8

On jette 6 fois de suite une pièce équilibrée.

1. Quelle est la probabilité d'obtenir au moins 5 fois «Pile»?
2. Quelle est la probabilité d'obtenir plus de «Pile» que de «Face»?
3. Quelle est la probabilité d'obtenir autant de «Pile» que de «Face»?
4. Quelle est la probabilité d'obtenir plus de 4 «Pile» consécutifs ou plus de 4 «Face» consécutifs?

Corrigé

L'univers est l'ensemble des 6-uplets de l'ensemble ${P, F}$. $\operatorname{Card} \Omega=2^{6}=64$. Il y a équiprobabilité.

1. Soit A : «on obtient au moins cing P ». On cherche $p(A)$.

On cherche tous les 6_uplets contenant 5 P et 1 F ou 6 P . Un tel 6_uplet est caractérisé par les rangs des P (l'ordre n'intervient pas), donc par une combinaison de 5 éléments parmi 6 , ou de 6 éléments parmi 6 . Par conséquent : $\operatorname{Card} A=\binom{6}{5}+\binom{6}{6}=6+1=7$. Donc : $p(A)=\frac{7}{64}$ 2. Soit B : « on obtient plus de P que de F ». On cherche $p(B)$.

On cherche tous les 6 _uplets contenant 4 P et 2 F , ou 5 P et 1 F , ou 6 P . Comme précédemment, on obtient : Card $\mathrm{B}=\binom{6}{4}+\binom{6}{5}+\binom{6}{6}=15+6+1=22$. Donc : $p(B)=\frac{22}{64}=\frac{11}{32}$. 3. Soit C : «on obtient plus de F que de P », et D : «on obtient autant de P que de F ». ${B, C, D}$ est une partition de $\Omega$, et il est clair que $p(B)=p(C)$. On obtient donc : $p(D)=1-2 p(B)=1-2 \frac{11}{32}=\frac{10}{32}$. La probabilité d'obtenir autant de «Pile» que de «Face» vaut $\frac{10}{32}$. 4. Supposons que l'on ait une série d'au moins 4 P . Elle contient donc une série d'exactement 4 P , ou 5 P , ou 6 P . Les 6-uplets favorables sont alors : pour 4 P : (P,P,P,P,F,P), (P,P,P,P,F,F), (F,P,P,P,P,F), (F,F,P,P,P,P), (P,F,P,P,P,P) pour 5 P : (P,P,P,P,P,F), (F,P,P,P,P,P) pour 6 P : ( $\mathrm{P}, \mathrm{P}, \mathrm{P}, \mathrm{P}, \mathrm{P}, \mathrm{P}$ ) Soit 8 cas en tout. Et on en trouve autant si l'on cherche les séries d'au moins 4 F . Par additivité, on obtient donc 16 cas favorables. Donc la probabilité d'obtenir plus de 4 «Pile» consécutifs ou plus de 4 «Face» consécutifs est $\frac{16}{64}=0,25$.

Exercice 9

On considère l'ensemble $E={a, b, c, d}$

1. Combien de parties a cet ensemble E?
2. Combien de parties à 2 éléments a cet ensemble E ?

Les énumérer toutes. 3. Le programme en Python qui suit permet d'afficher toutes ces parties à 2 éléments dans la console.

1L=['a','b','c','d']
2n = len(L)
3for i in range(n):
4 for j in
5 print('{',L[i],',',L[j] ,'}')

Compléter les lignes 4 et 5 de ce programme pour qu'il fonctionne correctement. 4. Combien de parties à 3 éléments a cet ensemble E ?

Les énumérer toutes. 5. Modifier le programme précédent pour qu'il puisse afficher toutes ces parties à 3 éléments dans la console.

Corrigé

1. On calcule $2^{4}=16$.

Comme E a 4 éléments, il possède donc 16 parties. 2. On calcule $\binom{4}{2}=6$.

E possède donc 6 parties à 2 éléments. Il s'agit de : ${a, b},{a, c},{a, d},{b, c},{b, d},{c, d}$. 3. Voici le programme modifié.

l L=['a','b','c','d']
2n = len(L)
3for i in range(n):
4 for j in range(i+1,n):
5 print('{',L[i],',',L[j],'}')

On notera que, quel que soit l'ordre dans lequel sont stockés les éléments de $E$ dans la liste, le programme affichera bien toutes les parties prévues... Par ailleurs, les experts auront remarqué que range(n-1) aurait suffi dans la ligne 3. En effet, lorsque $i$ vaut $n-1, j$ parcourt alors la séquence range( $n, n$ ) qui ne contient rien. 4. On calcule $\binom{4}{3}=4$.

E possède donc $\square$ 4 parties à 3 éléments. Il s'agit de :

$$ {a, b, c},{a, b, d},{a, c, d},{b, c, d} . $$

5. Voici le programme modifié pour qu'il puisse afficher toutes ces parties à trois éléments dans la console.

1L=['a','b','c','d']
2n = len(L)
3for i in range(n):
    for j in range(i+1,n):
        for k in range(j+1,n):
            print('{',L[i],',',L[j] ,',',L[k],'}')

Exercice 10

Tout entier naturel $n$ peut s'écrire sous la forme d'une somme unique de puissances de 2 comme suit : $n=a_{k} \times 2^{k}+a_{k-1} \times 2^{k-1}+a_{k-2} \times 2^{k-2}+\ldots+a_{2} \times 2^{2}+a_{1} \times 2^{1}+a_{0} \times 2^{0}$ où $k$ dépend de $n$, et où $a_{k}=1$, et où tous les $a_{i}$ pour $i$ entre 0 et $k-1$ valent soit 0 , soit 1 . Par exemple: $0=0 \times 2^{0} \quad 1=1 \times 2^{0} \quad 2=1 \times 2^{1}+0 \times 2^{0}$ $6=1 \times 2^{2}+1 \times 2^{1}+0 \times 2^{0} \quad 8=1 \times 2^{3}+0 \times 2^{2}+0 \times 2^{1}+0 \times 2^{0}$ $17=1 \times 2^{4}+0 \times 2^{3}+0 \times 2^{2}+0 \times 2^{1}+1 \times 2^{0}$ La suite des $a_{i}$ pour $i$ allant de $k$ à 0 donne l'écriture binaire du nombre $n$ considéré. En cas d'ambiguïté, l'indice (dec) ou (bin) permet de savoir si l'écriture considérée est décimale ou binaire. Par exemple: $\quad 0_{(\text {dec })}=0_{(\text {bin })} \quad 1_{(\text {dec })}=1_{(\text {bin })} \quad 2_{(\text {dec })}=10_{(\text {bin })}$ $6_{(\text {dec })}=110_{(\text {bin })} \quad 8_{(\text {dec })}=1000_{(\text {bin })} \quad 17_{(\text {dec })}=10001_{(\text {bin })}$

1. Donner l'écriture binaire de 13 .
2. Donner l'écriture décimale de $10101_{\text {(bin) }}$.
3. En Python, l'instruction L.reverse() retourne la liste $L$ en ayant inversé l'ordre de ses éléments. Par exemple, si $L=[1,2,3]$, alors $L$.reverse() retourne [3,2,1].

En Python, l'instruction $\mathbf{a} / / \mathbf{b}$ retourne le quotient de la division euclidienne de a par b.

En Python, l'instruction $\mathbf{a % b}$ retourne le reste de la division euclidienne de a par b.

Une suite de division euclidiennes par 2 fournit l'écriture binaire de n'importe quel naturel. Il suffit de noter les restes successifs, qui donneront dans l'ordre $a_{0}, a_{1}$, ...etc. Par exemple : $6=2 \times 3+0$ donne $a_{0}=0$, puis : $3=2 \times 1+1$ donne $a_{1}=1$, puis : $1=2 \times 0+1$ donne $a_{2}=1$. On vient de montrer que : $6=1 \times 2^{2}+1 \times 2^{1}+0 \times 2^{0}$. Et par là : $6_{(\text {dec })}=110_{(\text {bin })}$.

Écrire en Python une fonction binaire(x) qui retourne une liste du type $\left[a_{k}, a_{k-1}, \ldots, a_{1}, a_{0}\right]$ donnant l'écriture en binaire de l'entier naturel $x$. Par exemple, binaire(6) retourne [1,1,0] 4. Une écriture binaire peut être précédée d'autant de 0 que l'on veut.

Par exemple, 110 et 00110 codent toutes les deux le nombre 6. Écrire en Python une fonction binaireF(x,n) qui retourne une liste de longueur n donnant l'écriture en binaire de l'entier naturel $x$; la liste commencera donc éventuellement par des 0. Par exemple, binaire $\boldsymbol{F}(\mathbf{6 , 5})$ retourne [0,0,1,1,0] 5. L'écriture binaire d'un entier naturel étendue à n chiffres correspond à un n -uplet.

Par exemple, $6_{(\text {dec })}=110_{(\text {bin })}$ correspond au 3 -uplet ( $1,1,0$ ). Et $6_{(\text {dec })}=00110_{(\text {bin })}$ correspond au 5-uplet (0,0,1,1,0).

Écrire en Python une fonction liste_n_uplet(n) qui retourne une liste de tous les $n$-uplets de ${0,1}$. Par exemple, liste_n_uplet(2) retourne [[0, 0], [0, 1], [1, 0], [1, 1]]. 6. Écrire en Python une fonction parties(L) qui retourne une liste du type $\left[L_{1}, L_{2}, \ldots, L_{p}\right]$, où $L$ est une liste donnant les éléments d'un ensemble E , où $p$ est le nombre de parties de E , où $L_{1}, L_{2}, \ldots, L_{p}$ sont des listes donnant les éléments des différentes parties de E . Par exemple, si $E={1,2}$, alors $L=[1,2]$, et parties (L) retourne la liste [ [] , [2] , [1] , [1, 2] ].

Vérifier que votre programme est correct en affichant les parties de $E={1,2,3}$.

Corrigé

1. On a : $13=8+4+1=1 \times 2^{3}+1 \times 2^{2}+0 \times 2^{1}+1 \times 2^{0}$.

Donc : $13_{(\text {dec })}=1101_{(\text {bin })}$. 2. On considère $10101_{(\text {bin })}$. On calcule alors : $1 \times 2^{4}+0 \times 2^{3}+1 \times 2^{2}+0 \times 2^{1}+1 \times 2^{0}=16+4+1=21$. Donc : $10101_{(\text {bin })}=21_{[\text {dec })}$. 3. Voici une fonction binaire(n) qui retourne une liste donnant l'écriture en binaire de l'entier naturel $n$.

ldef binaire(a): # renvoie une liste contenant l'écriture binaire de a
    L=[a % 2]
    while a//2!=0:
        a=a//2
        L.append(a % 2)
    L.reverse()
    return L

4. Voici une fonction binaireF( $\mathbf{x}, \mathbf{n}$ ) qui retourne une liste de longueur n donnant l'écriture en binaire de l'entier naturel $x$.

9# binaireF(a,n) renvoie une liste de longueur n donnant l'écriture binaire de a
def binaireF(a,n):
    L=[a % 2]
    while a//2!=0:
        a=a//2
        L.append(a % 2)
    while len(L)<n:
        L.append(0)
    L.reverse()
    return L

On aurait pu utiliser l'instruction $\boldsymbol{L}=$ binaire(a) à l'intérieur de cette définition pour remplacer les lignes 11 à 14, mais il aurait fallu ensuite utiliser l'instruction L.reverse() pour de nouveau inverser l'ordre des éléments de L, ce qui n'est pas très habile... 5. Voici une fonction liste_n_uplet(n) qui retourne une liste de tous les n-uplets de ${0,1}$.

# binaireF(a,n) renvoie une liste de longueur n donnant l'écriture binaire de a
def liste_n_uplet(n):
    L=[]
    nombre=2**n
    for i in range (nombre):
        L.append(binaireF(i,n))
    return L

La variable nombre contient le nombre de n-uplets à générer. Chacun d'eux est associé à l'écriture binaire à n chiffres d'un naturel compris entre 0 et nombre - 1 . Par exemple, liste_n_uplet(2) retourne une liste de tous les 2-uplets de ${0,1}$. Ces 2 -uplets sont $2^{2}=4$. Le premier $(0,0)$ est associé à $0_{(d e c)}=00_{(\text {bin })}$. Le second $(0,1)$ associé à $1_{(\mathrm{dec})}=01_{(\mathrm{bin})}$. Le troisième $(1,0)$ associé à $2_{(d e c)}=10_{(\text {bin })}$. Le quatrième $(1,1)$ associé à $3_{(\text {dec })}=11_{(\text {bin })}$. 6. Voici une fonction parties(L) qui retourne une liste donnant les parties de l'ensemble associé à L .

28# parties(L) renvoie une liste donnant les parties de l'ensemble associé à L
29 def parties(L):
    n=len(L)
    l_binaire=liste_n_uplet(n)
    n_parties=len(l_binaire)
    ensemble=[]
    for i in range(n_parties):
        partie=[]
        for k in range(n):
            if l_binaire[i][k]==1:
                partie.append(L[k])
        ensemble.append(partie)
    return ensemble

Pour afficher les parties de $E={1,2,3}$, il suffit d'ajouter ces deux lignes à la suite du fichier donnant les fonctions précédentes, et d'exécuter le programme.

44L=[1,2,3]
45 print(parties(L))

Il s'affiche dans la console : [[], [3], [2], [2, 3], [1], [1, 3], [1, 2], [1, 2, 3]] On peut aussi taper les mêmes instructions directement dans la console.

Et voici un programme pour les experts !

# transforme une liste d'entiers en chaîne donnant une partie
# exple: (1,2) devient '{1,2}'
def ecriture(L):
    s = '{'+','.join(str(elem) for elem in L)+'}'
    return s
# parties(L) renvoie une liste donnant les parties de l'ensemble associé à L
def parties(L):
    n=len(L)
    l_binaire=liste_n_uplet(n)
    n_parties=len(l_binaire)
    ensemble=[]
    for i in range(n_parties):
        partie=[]
        for k in range(n):
            if l_binaire[i][k]==1:
                partie.append(L[k])
        ensemble.append(ecriture(partie))
    return ensemble
L=[1,2,3]
ens=' '.join(parties(L))
print(ens)

Le programme qui précède propose un affichage plus convivial des parties de l'ensemble E , à condition que E soit constitué d'entiers naturels. Si $\boldsymbol{L}$ est une liste dont les éléments sont des chaînes de caractères, alors l'instruction 'truc'.join(L) retourne une chaîne composée des éléments de $L$ séparés par la chaîne 'truc'. Par exemple, si $L=($ 'un','bizarre'), alors 'truc'.join( $L$ ) renvoie 'un truc bizarre' Notre programme affiche $}{3}{2}{2,3}{1}{1,3}{1,2}{1,2,3}$ dans la console.

Exercice 11

Soit $\left(u_{n}\right)$ la suite définie pour tout naturel $n$ par $u_{n}=\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\ldots+\frac{1}{n!}$. On peut aussi utiliser l'écriture $u_{n}=\sum_{k=0}^{n} \frac{1}{k!}$.

Partie A

1. Démontrer que ( $u_{n}$ ) est strictement croissante.
2. Démontrer par récurrence sur $n$ que, pour tout naturel $n$ non nul, on a : $\frac{1}{n!} \leq \frac{1}{2^{n-1}}$
3. Montrer que, pour tout naturel $n$, on a : $u_{n} \leq 3-2 \times 0,5^{n}$
4. En déduire que la suite $\left(u_{n}\right)$ est convergente.

Partie B

On va conjecturer la valeur de la limite de la suite $\left(u_{n}\right)$ grace à un algorithme.

1. Écrire en Python une fonction factorielle(n) qui retourne la valeur de $n$ ! pour tout naturel $n$. Vous utiliserez la fonction factorielle définie précédemment.
2. Écrire en Python une fonction $\mathbf{u}(\mathbf{n})$ qui retourne la valeur de $u_{n}$ pour tout naturel $n$.
3. Quelles sont les valeurs de $u(5), u(10), u(100)$ et $u(1000)$ retournées par votre programme? Conjecturer la valeur de $\lim {n \rightarrow+\infty} u{n}$.
4. On pose $l=\lim {n \rightarrow+\infty} u{n}$, et on admet que la valeur conjecturée à la question précéente est correcte. Écrire en Python une fonction min(delta) qui retourne le plus petit entier $n$ à partir duquel $\left|u_{n}-l\right| \leq$ delta, où delta est un réel strictement positif.
5. Jean affirme qu'un tel entier $n$ existe car $\left(u_{n}\right)$ est strictement croissante.

Jean a-t-il raison?

Corrigé

Partie A

1. Soit $n$ un naturel.

On a : $u_{n+1}-u_{n}=\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\ldots+\frac{1}{n!}+\frac{1}{(n+1)!}-\frac{1}{0!}-\frac{1}{1!}-\frac{1}{2!}-\ldots-\frac{1}{n!}$ Soit : $u_{n+1}-u_{n}=\frac{1}{(n+1)!}$ Or le résultat est strictement positif. Et c'est vrai pour tout naturel $n$. Donc ( $u_{n}$ ) est strictement croissante. 2. Soit $P_{n}: \frac{1}{n!} \leq \frac{1}{2^{n-1}}$.

Démontrons par récurrence que, pour tout naturel $n$ non nul, la propriété $P_{n}$ est vraie. Initialisation : On a : $\frac{1}{1!}=1$ et $\frac{1}{2^{1-1}}=\frac{1}{2^{0}}=1$. On a bien $\frac{1}{1!} \leq \frac{1}{2^{1-1}}$. Donc $P_{1}$ est vraie.

Hérédité :

Soit $n$ un entier naturel non nul, supposons que $P_{n}$ soit vraie. On a donc : $\frac{1}{n!} \leq \frac{1}{2^{n-1}}$. Donc : $\frac{1}{n+1} \times \frac{1}{n!} \leq \frac{1}{n+1} \times \frac{1}{2^{n-1}}$ (on a multiplié chaque membre par un nombre strictement positif $\left.\frac{1}{n+1}\right)$. On obtient donc : $\frac{1}{(n+1)!} \leq \frac{1}{(n+1) \times 2^{n-1}}$.

Or, comme $1 \leq n$, on a: $2 \leq n+1$, et donc : $2 \times 2^{n-1} \leq(n+1) \times 2^{n-1}$. Et par là : $\frac{1}{(n+1) \times 2^{n-1}} \leq \frac{1}{2 \times 2^{n-1}}$ (deux nombres strictement positifs et leurs inverses sont dans l'ordre inverse). Soit : $\frac{1}{(n+1) \times 2^{n-1}} \leq \frac{1}{2^{n}}$.

Par conséquent, on en déduit finalement que $: \frac{1}{(n+1)!} \leq \frac{1}{2^{n}}$. Donc $P_{n+1}$ est vraie. Conclusion : pour tout naturel $n$ non nul, $\frac{1}{n!} \leq \frac{1}{2^{n-1}}$. 3. D'après le résultat précédent, pour tout naturel $k$ non nul, on a : $\frac{1}{k!} \leq \frac{1}{2^{k-1}}$. Donc, pour tout naturel $n$ non nul : $\frac{1}{1!}+\frac{1}{2!}+\ldots+\frac{1}{n!} \leq \frac{1}{2^{1-1}}+\frac{1}{2^{2-1}}+\ldots+\frac{1}{2^{n-1}}$. Or : $1+q+q^{2}+\ldots+q^{n-1}=\frac{1-q^{n}}{1-q}$ pour $q \neq 1$. Ici : $q=\frac{1}{2}$, et par là, on a, on obtient : $\frac{1}{1!}+\frac{1}{2!}+\ldots+\frac{1}{n!} \leq \frac{1-\left(\frac{1}{2}\right)^{n}}{1-\frac{1}{2}}$. Soit : $\frac{1}{1!}+\frac{1}{2!}+\ldots+\frac{1}{n!} \leq \frac{1-0,5^{n}}{\frac{1}{2}}$. Soit : $\frac{1}{1!}+\frac{1}{2!}+\ldots+\frac{1}{n!} \leq 2\left(1-0,5^{n}\right)$. Et par là, en sommant 1 à chaque membre : $u_{n} \leq 1+2\left(1-0,5^{n}\right)$. Soit : $u_{n} \leq 3-2 \times 0,5^{n}$. Ceci est également vrai pour $n=0$ (car $u_{0}=1$ et $3-2 \times 0,5^{0}=1$ ). Finalement : pour tout naturel $n$, on a : $u_{n} \leq 3-2 \times 0,5^{n}$. 4. Comme $u_{n} \leq 3-2 \times 0,5^{n}$, on en déduit immédiatement que : $u_{n} \leq 3$.

La suite ( $u_{n}$ ) est donc majorée. Or la suite $\left(u_{n}\right)$ est strictement croissante. Donc la suite ( $u_{n}$ ) est convergente.

Partie B

1. Voici une fonction factorielle(n) qui retourne la valeur de $n$ ! pour tout naturel $n$.

def factorielle(n):
    y=1
    for k in range(1,n+1):
        y=y*k
    return y

2. Voici une fonction $\mathbf{u}(\mathbf{n})$ qui retourne la valeur de $u_{n}$ pour tout naturel $n$.

def factorielle(n):
    y=1
    for }k\mathrm{ in range(1,n+1):
        y=y*k
    return y
def u(n):
    y=0
    for k in range(n+1):
        y=y+1/factorielle(k)
    return y
from math import exp
def min(delta):
    n=0
    e=exp(1)
    while abs(u(n)-e)>delta:
        n=n+1
    return n

On aurait pu commencer le programme par from math import factorial et remplacer factorielle(k) par factorial(k) dans le programme, mais cela n'aurait pas respecté l'énoncé ! 3. Le programme nous donne : $u(5) \approx 2.7166666666666663$ $u(10) \approx 2.7182818011463845$ $u(100) \approx 2.7182818284590455$ et $u(1000) \approx 2.7182818284590455$

On conjecture que $\lim {n \rightarrow+\infty} u{n}=e$. 4. Voici une fonction min(delta) qui retourne le plus petit entier $n$ à partir duquel $\left|u_{n}-l\right| \leq$ delta, où delta est un réel strictement positif.

14 from math import exp
15def min(delta):
16 n=0
17 e=exp(1)
18 while abs(u(n)-e)>delta:
19 n=n+1
20 return n

Évidemment, pour que Python comprenne ce que représente $\exp (1)$, il suffit de commencer le programme par from math import exp. 5. Jean affirme qu'un tel entier $n$ existe car ( $u_{n}$ ) est strictement croissante.

Jean a tort. Un tel entier $n$ existe car $\lim {n \rightarrow+\infty} u{n}=e$.

Le fait que ( $u_{n}$ ) soit strictement croissante nous assure que le programme proposé renvoie bien le plus petit entier convenable.

Exercice 12

On répartit au hasard 4 boules numérotées de 1 à 4 dans 5 tiroirs étiquetés $\mathrm{a}, \mathrm{b}, \mathrm{c}, \mathrm{d}$ et e. Calculer les probabilités des événements suivants : A : «un des tiroirs contient exactement 4 boules » B : « un des tiroirs contient exactement 3 boules » C: «aucun tiroir ne contient plus d'une boule» D: «un tiroir contient 2 boules, et les autres ne contiennent pas plus d'une boule» E: «deux tiroirs contiennent chacun exactement 2 boules» F : «aucun tiroir ne contient plus de 2 boules »

Corrigé

La répartition des boules se ramène à un 4-uplet de ${a, b, c, d, e}$. Par exemple, le 4-uplet ( $a, e, a, d$ ) correspond au fait que le tiroir a contient les boules 1 et 3 , le tiroir e contient la boule 2, et le tiroir d contient la boule 4. On calcule : $5^{4}=625$. Il y a donc 625 répartitions possibles et équiprobables. Cherchons $\mathrm{p}(\mathrm{A})$. Le choix du tiroir qui contient les 4 boules donne le 4-uplet favorable. Il ya donc 5 cas possibles. Donc $p(A)=\frac{5}{625}=0,008$.

Cherchons $\mathrm{p}(\mathrm{B})$. Pour construire un 4-uplet favorable, on choisit la boule placée seule dans un tiroir, puis le tiroir qui la contient, puis le tiroir qui contient les 3 boules. On a $C$ ard $B=4 \times 5 \times 4=80$ Donc $p(B)=\frac{80}{625}=0,128$.

Cherchons $\mathrm{p}(\mathrm{C})$. Un 4-uplet favorable est un arrangement de ${a, b, c, d, e}$. On a $C$ ard $C=5 \times 4 \times 3 \times 2=120$ Donc $p(C)=\frac{120}{625}=0,192$.

Cherchons p(D). Pour construire un 4-uplet favorable, on choisit les 2 boules placées ensemble dans un tiroir, puis le tiroir qui les contient, puis le tiroir qui contient la boule restante de numéro le plus faible, puis le tiroir qui contient l'autre boule restante.

On a $C$ ard $D=\binom{4}{2} \times 5 \times 4 \times 3=360$ Donc $p(D)=\frac{360}{625}=0,576$.

Cherchons $\mathrm{p}(\mathrm{E})$. Pour construire un 4-uplet favorable, on choisit le tiroir dans lequel est placée la première boule, puis la boule qui est avec elle, puis le tiroir qui contient les 2 autres boules. On a $C$ ard $E=5 \times 3 \times 4=60$ Donc $p(D)=\frac{60}{625}=0,096$.

Cherchons $\mathrm{p}(\mathrm{F})$. On a : $F=C \cup D \cup E$, et comme ces événements sont incompatibles deux à deux, on obtient: $p(F)=p(C)+p(D)+p(E)=0,864$. Autre méthode : $F$ est le contraire de $A \cup B$ avec A et B incompatibles. Donc : $p(F)=1-p(A)-p(B)=0,864$.