Cours : Fonction logarithme népérien

Fonction logarithme népérien

Définition et propriété

La fonction logarithme népérien, notée ln, est la fonction définie sur ] $0 ;+\infty$ [ qui, à tout réel strictement positif $b$ associe l'unique solution de l'équation $e^{x}=b$. Ainsi, pour tout réel $b$ strictement positif, pour tout réel $a$, $\qquad$ $a=\ln b \Leftrightarrow e^{a}=b$ . Et par là, on obtient, en particulier : $\ln 1=0 \quad \ln e=1$.

Propriété

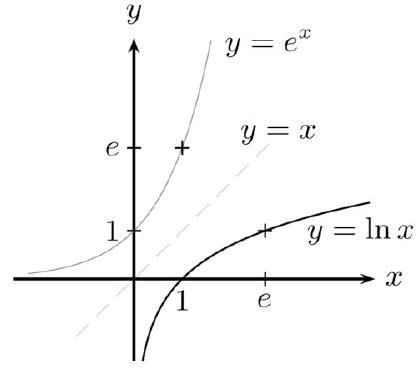
Dans un repère orthonormé, les courbes représentatives des fonction $\ln x$ et $e^{x}$ sont symétriques par rapport à la droite d'équation $y=x$.

Dérivées

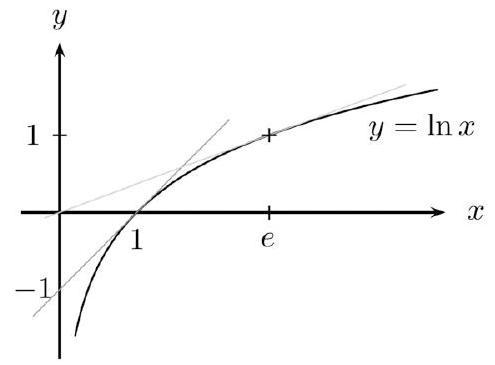
La fonction $\ln x$ admet pour dérivée $\frac{1}{x}$ sur $] 0 ;+\infty\left[\right.$. Ainsi : $(\ln x)^{\prime}=\frac{1}{x}$.

Soit $u$ une fonction strictement positive sur un intervalle I. La fonction $\ln u$ admet pour dérivée $\frac{u^{\prime}}{u}$ sur I. Ainsi : $(\ln u)^{\prime}=\frac{u^{\prime}}{u}$.

Conséquence : Les fonctions $u$ et $\ln u$ ont même sens de variation sur I.

Propriétés

La fonction $\ln x$ est continue sur $] 0 ;+\infty[$. $\ln x$ est strictement négative sur $] 0 ; 1[$. $\ln x$ est strictement positive sur $] 1 ;+\infty[$.

Chapitre 5

La fonction $\ln x$ est strictement croissante.

Limites de référence

$\lim _{x \rightarrow+\infty} \ln x=+\infty \quad \lim _{x \rightarrow 0} \ln x=-\infty$ $\lim _{x \rightarrow 0} x \ln x=0$ $\lim _{x \rightarrow+\infty} \frac{\ln x}{x}=0 \quad \lim _{x \rightarrow+\infty} \frac{\ln x}{x^{n}}=0 \quad($ pour $n \in \mathbb{N}$ et $n>0)$ $\lim _{x \rightarrow 0} \frac{\ln (1+x)}{x}=1$

Propriétés

Pour tous nombres réels strictement positifs $a$ et $b$, pour tout entier relatif $p$, on a : $\ln a b=\ln a+\ln b$ $\ln \frac{a}{b}=\ln a-\ln b$ $\ln a^{p}=p \ln a$ $\ln \sqrt{a}=\frac{1}{2} \ln a$

Pour tous nombre réel $a$, on a: $\ln \left(e^{a}\right)=a$ Pour tous nombre réel strictement positif $a$, on a : $\quad e^{\ln a}=a$

Propriétés

Pour tous nombres réels strictement positifs $a$ et $b$, on a : $\ln a<\ln b \Leftrightarrow a<b \quad$ et $\quad \ln a=\ln b \Leftrightarrow a=b$.

Savoir faire

Comment résoudre les équations et les inéquations où apparaît la fonction In ou la fonction exponentielle? En général, il suffit d'isoler le terme contenant la fonction problématique, puis de composer chaque membre de l'équation ou de l'inéquation par la fonction réciproque.